이진탐색
개요
이진탐색이란?
- 배열 내부의 데이터들 중, 특정 데이터를 찾아내는 알고리즘이다.
- 배열 내부의 데이터가 정렬되어 있어야만 사용할 수 있는 알고리즘이다.
- 이진 탐색은 위치를 나타내는 변수 3개를 사용한다.
- 탐색 범위의 시작점
- 탐색 범위의 끝점
- 탐색 범위의 중간점
- 찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾아내는 것이 이진 탐색 과정이다.
이진탐색 동작 과정
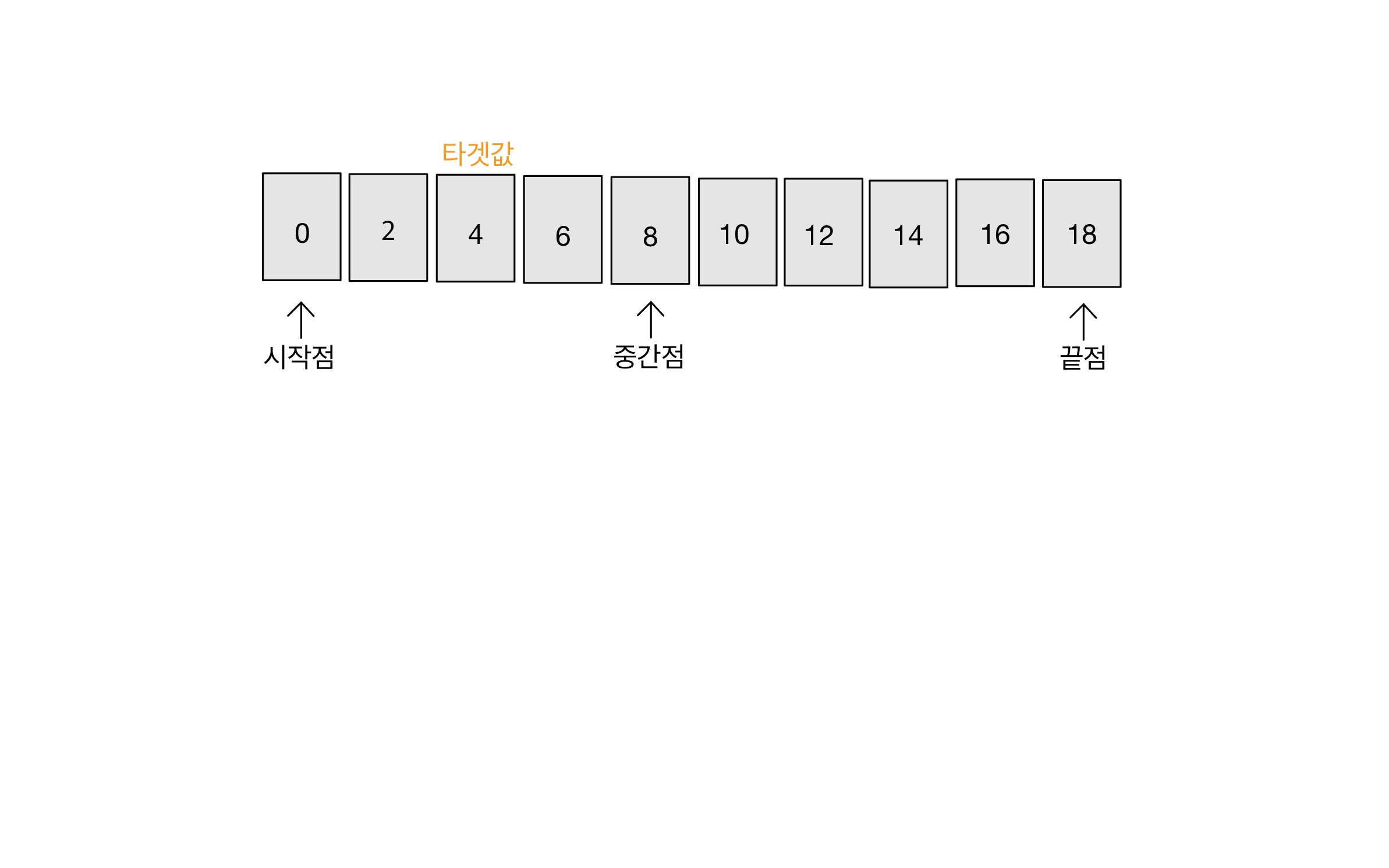
- 탐색 범위의 시작점, 끝점, 중간점을 설정한다.
- 중간점 = (시작점+끝점)/2
- 중간점이 실수 형태인 경우, 소수점 이하는 버린다.
- 찾으려는 값(target)과 중간점에 위치한 값을 비교한다.
target 값 < 중간점의 값: 3번을 수행한다.target 값 > 중간점의 값: 4번을 수행한다.target 값 = 중간점의 값: 5번을 수행한다.
- 시작점, 끝점, 중간점을 아래와 같이 설정한다. 그리고 2번으로 돌아간다.
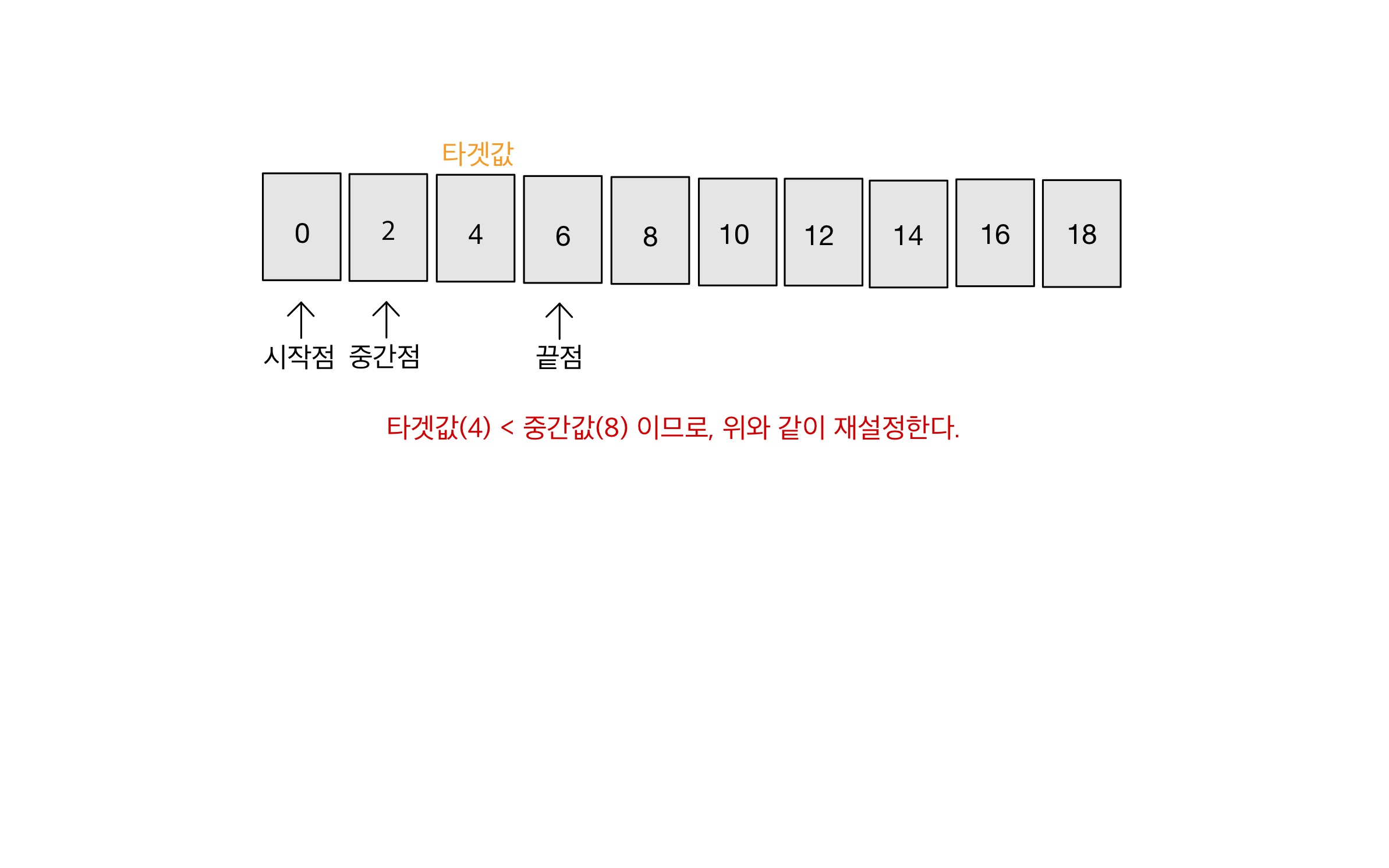
- 시작점 = ‘이전의 중간점’ + 1
- 끝점 = 변경 X
- 중간점 = (‘이전의 중간점’ + ‘끝점’ + 1) / 2
이때 소수점 이하는 버린다.
- 시작점, 끝점, 중간점을 아래와 같이 설정한다. 그리고 2번으로 돌아간다.
- 시작점 = 변경 X
- 끝점 = ‘이전의 중간점’ - 1
- 중간점 = (‘이전의 중간점’ + ‘시작점’ - 1) / 2
이때 소수점 이하는 버린다.
- target값을 찾아냈으므로 알고리즘을 종료한다.
예시
예시에서 사용할 배열 형태

Step 01
Step 02
Step 03
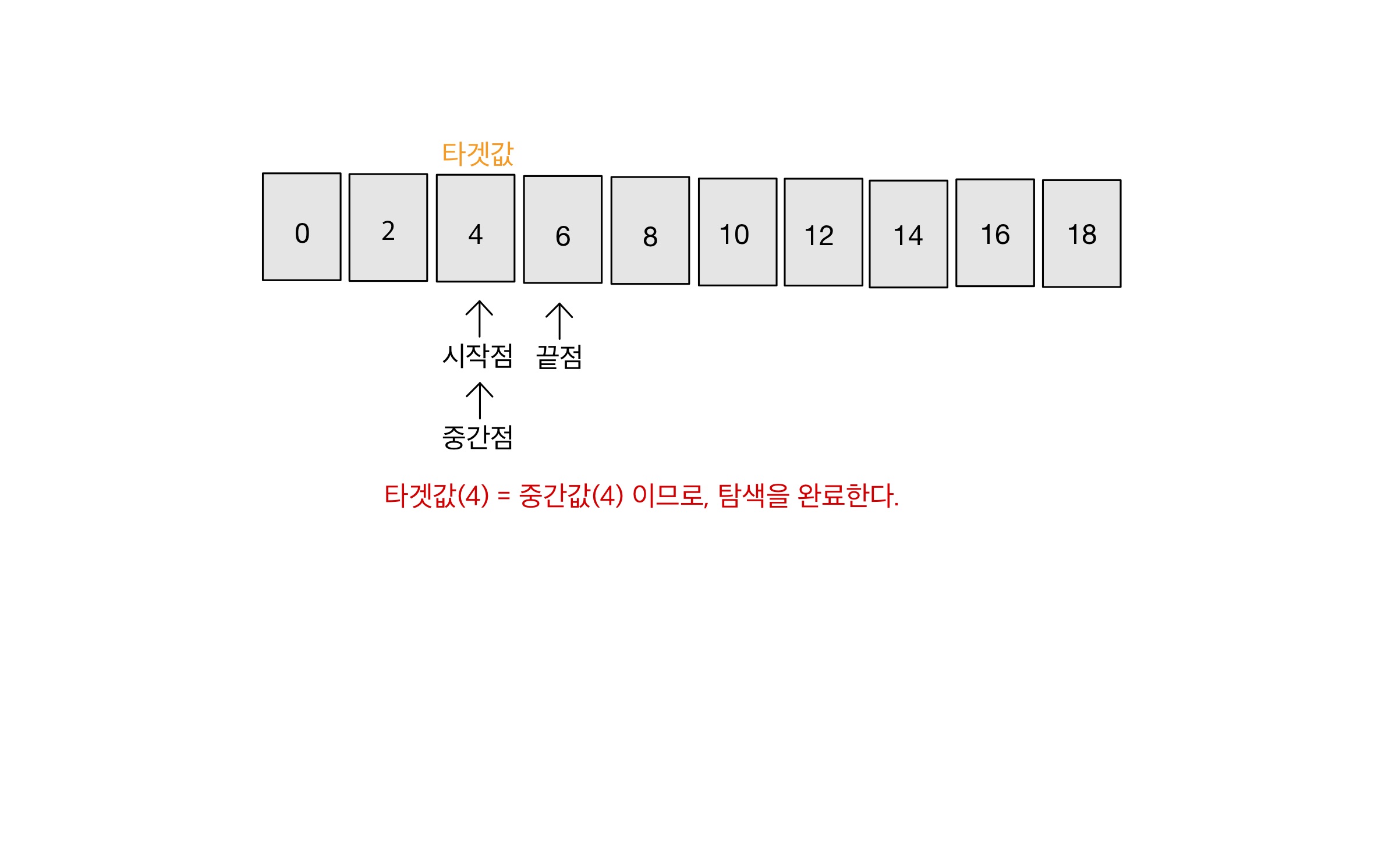
결과
- 타겟값(4)가 index 2번에 존재함을 알아낼 수 있다.
- 이때 타겟값의 index은 중간점과 같다.
특징
- 이진 탐색을 이용해 총 3번의 탐색으로 원소를 찾을 수 있다.
- 이진 탐색은 한번 확인할 때마다 확인하는 원소의 개수가 절반씩 줄어든다는 점에서 시간 복잡도가
O(logn)이다. - 이진탐색을 구현하는 방법에는 2가지가 존재한다.
- 재귀함수를 사용하는 방법
- 반복문을 사용하는 방법
소스코드 - 재귀 방식
이진탐색 알고리즘
public class 이진탐색_재귀 {
private static void solution(int[] n, int start, int end, int middle, int target) {
if (start == end && n[middle] != target) {
System.out.println("찾으려는 값이 존재하지 않습니다.");
return;
}
if (n[middle] < target) {
solution(n, middle+1, end, (middle+1+end)/2, target);
} else if (n[middle] > target) {
solution(n, start, middle - 1, (start + middle - 1) / 2, target);
} else {
System.out.println(middle);
return;
}
}
public static void execute() {
int[] n = {0, 2, 4, 6, 8, 10, 12, 14, 16, 18};
solution(n, 0, 9, 9/2, 5);
}
}
출력결과
2
소스코드 - 반복문 방식
이진탐색 알고리즘
public class 이진탐색_반복문 {
private static void solution(int[] n, int target) {
int start = 0;
int end = n.length - 1;
int middle = (start+end)/2;
while (true) {
if (start == end && n[middle] != target) {
System.out.println("찾으려는 값이 존재하지 않습니다.");
return;
}
if (n[middle] > target) {
end = middle - 1;
middle = (start + end) / 2;
} else if (n[middle] < target) {
start = middle + 1;
middle = (start+end) / 2;
} else if (n[middle] == target) {
break;
}
}
System.out.println(middle);
}
public static void execute() {
int[] n = {0, 2, 4, 6, 8, 10, 12, 14, 16, 18};
solution(n, 5);
}
}
출력결과
2
- 나동빈, 『이것이 코딩 테스트다』
