logo img Dev Blog

[알고리즘 - 조합] 조합과 조합 알고리즘

February 20, 2022

조합 알고리즘

개요

  • 조합 알고리즘에 대해 알아보기 전에, 먼저 조합에 대해 알아보자.


조합이란?

  • n개의 숫자 중, r개의 숫자를 순서없이 뽑는 것


공식

  • 공식
  • ‘하나의 원소를 선택할 경우’ + ‘하나의 원소를 선택하지 않을 경우’의 합이다.
  • 즉, n개 중 r개를 뽑는 경우의 수는 ‘하나의 원소를 선택하고 나머지를 뽑는 경우’와 ‘하나의 원소를 제외하고 뽑는 경우’로 이루어진다.

    자세한 것은 아래 예시를 통해 설명한다.


예시

주어진 배열

  • {1, 2, 3}

    뽑는 개수 (r)

  • 2개

    가능한 조합

  • {1, 2} , {1, 3}, {2, 3}

    공식 적용

  • 공식


  • 공식 인 이유?
    • 3개 중 하나는 뽑아두고(n-1), 남은 횟수(r-1)만큼 마저 뽑는다.
    • 예시
      • 1을 뽑아둔다. → 남은 원소 = 3-1 = 2 = n-1
      • 남은 횟수만큼 뽑는다. → 남은 횟수 = 2-1 = 1


  • 공식 인 이유?
    • 3개 중 하나를 제외하고(n-1), 뽑는다.
    • 예시
      • 1을 제외한다. → 남은 원소 = 3-1 = 2 = n-1
      • 뽑는다. → 2 = r


  • 따라서 해당 공식을 공식 이 나올때까지 반복하면, 공식 을 구할 수 있다.



조합 알고리즘

조합의 경우의 수 구하기

  • 조합의 실제 경우를 구하는 것이 아닌, 단순히 경우의 수 만 구하는 알고리즘에 대해 먼저 알아보자.


코드

public class 조합_경우의_수 {

  public int getCombinationCaseNum(int n, int r) {

    /*
     * n == r 이라면, 모두 뽑는 경우 하나만 존재한다.
     * r == 0 이라면, 모두 뽑지 않는 경우 경우 하나만 존재한다.
     */
    if (n == r || r == 0) {
      return 1;
    }

    return getCombinationCaseNum(n-1, r-1) + getCombinationCaseNum(n-1, r);
  }

}
  • 코드가 상당히 단순하다.
  • 단순히 총 경우의 개수만 구한다면, 공식을 코드화하면 된다.


실제 조합 구하기

  • 이번에는 실제 조합을 구해보자.
  • 배열의 처음부터 마지막까지 돌며 아래 케이스를 모두 고려해야 한다.
    1. 현재 인덱스의 원소를 선택하는 경우 (공식)
    2. 현재 인덱스의 원소를 선택하지 않는 경우 (공식)
  • 재귀를 통한 완전탐색 방식으로 실제 조합을 구할 수 있다.
    • 백트래킹 등의 방식도 있지만, 생략한다.
  • 코드를 통해 설명하겠다.


코드

코드는 한번 훑어본 뒤, 아래 설명을 참고하자. 그리고 다시 코드를 보자.

public class 조합_구하기 {

  public static void getCombination(int[] numAry, boolean[] visited, int depth, int n, int r) {
    if (r == 0) { //뽑아야하는 만큼 뽑았으므로, 출력 후 종료
      print(numAry, visited);
      return;
    }
    if (depth == n) { //모든 원소를 둘러보았으므로, 종료
      return;
    }

    visited[depth] = true; //현재 원소를 뽑았을 때
    getCombination(numAry, visited, depth+1, n, r-1); // n-1Cr-1

    visited[depth] = false; //현재 원소를 뽑지 않았을 때
    getCombination(numAry, visited, depth+1, n, r); // n-1Cr
  }

  //뽑은 원소를 출력하는 메서드
  private static void print(int[] numAry, boolean[] visited) {
    System.out.print("{");
    for (int i = 0; i < visited.length; i++) {
      if (visited[i]) {
        System.out.print(numAry[i] + " ");
      }
    }
    System.out.print("}\n");
  }
}
  • 변수 depth
    • 현재 인덱스를 가르킨다.
    • 순열이 아닌 조합이기 때문에, 이전에 살펴본 원소는 더이상 고려대상이 아니다.
      따라서 변수 depth 는 무조건 1씩 증가한다.
      • 즉 이전에 뽑을지 말지 판단했던 원소는 다음 뽑기에서 제외된다. (뽑지 않더라도)


  • 배열 boolean[] visited
    • visited[i] = i번째 원소를 뽑을지, 말지에 대한 정보
    • 현재 인덱스(depth)에 위치한 원소를 뽑는다면 → visited[depth] = true
    • 현재 인덱스(depth)에 위치한 원소를 뽑지 않는다면 → visited[depth] = false


  • 매개변수 n
    • 조합 공식에선 n-1을 사용한다. 하지만 위 코드에선 매개변수 n은 변화하지 않는다.
    • 왜냐하면, 변수 depth 가 1씩 증가하므로, n 이 1씩 감소될 필요가 없기 때문이다.


  • 재귀 종료 조건
    • depth == n
      • 모든 원소를 살펴보았으므로 종료한다.
      • 단 depth == n 이더라도, 뽑아야하는 횟수만큼 뽑았다는 보장이 없기 때문에 뽑은 원소를 출력하지는 않는다.
    • r == 0
      • 뽑아야하는 횟수만큼 뽑았으므로 종료한다.
      • 뽑아야하는 횟수만큼 뽑았기 때문에, 뽑은 원소를 출력한다.
        • 이때 visited 배열에서 true인 index가 ‘뽑은 원소의 index’이다.


재귀의 흐름

1.

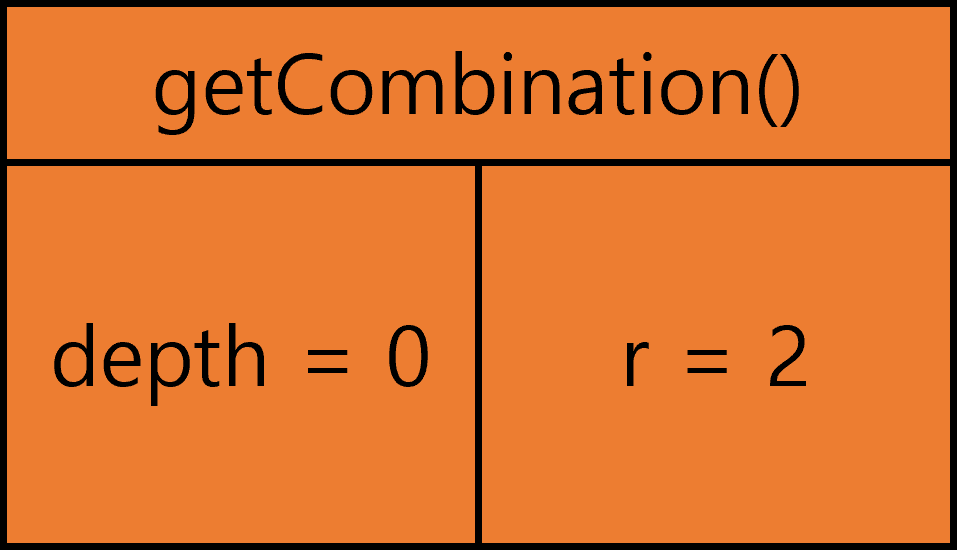
2.

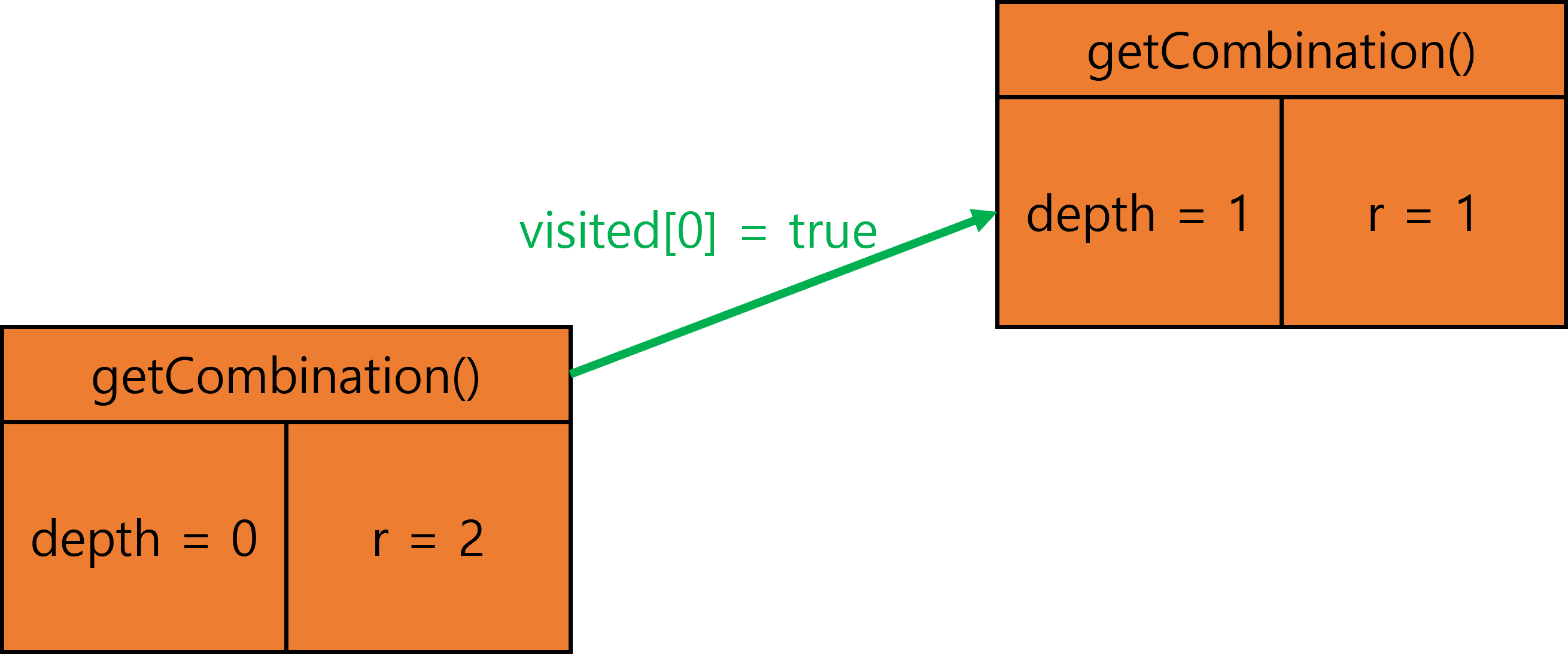
3.

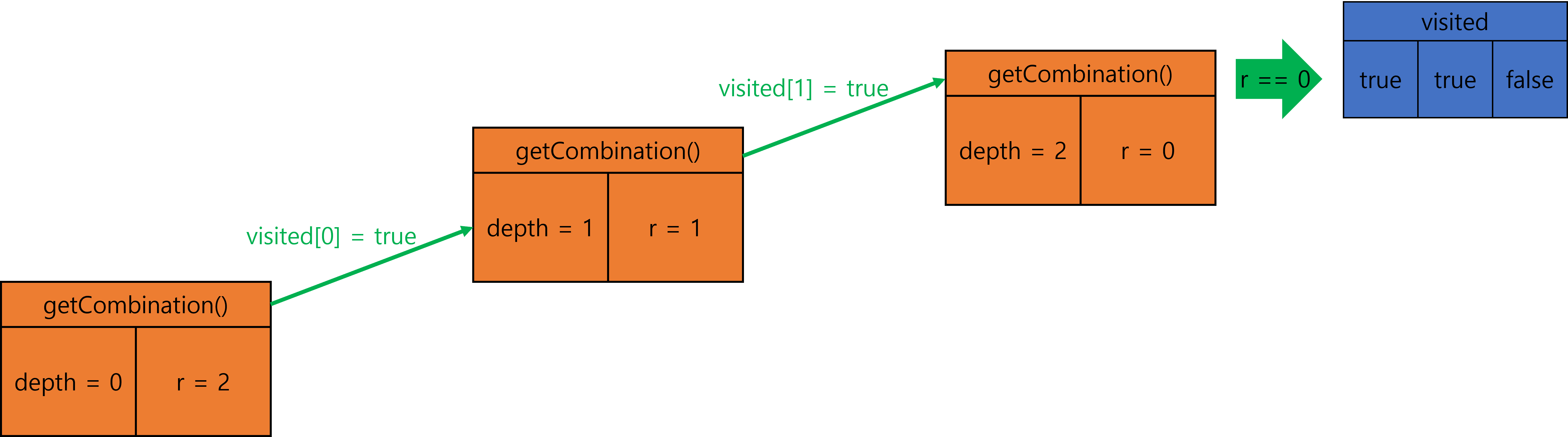
4.

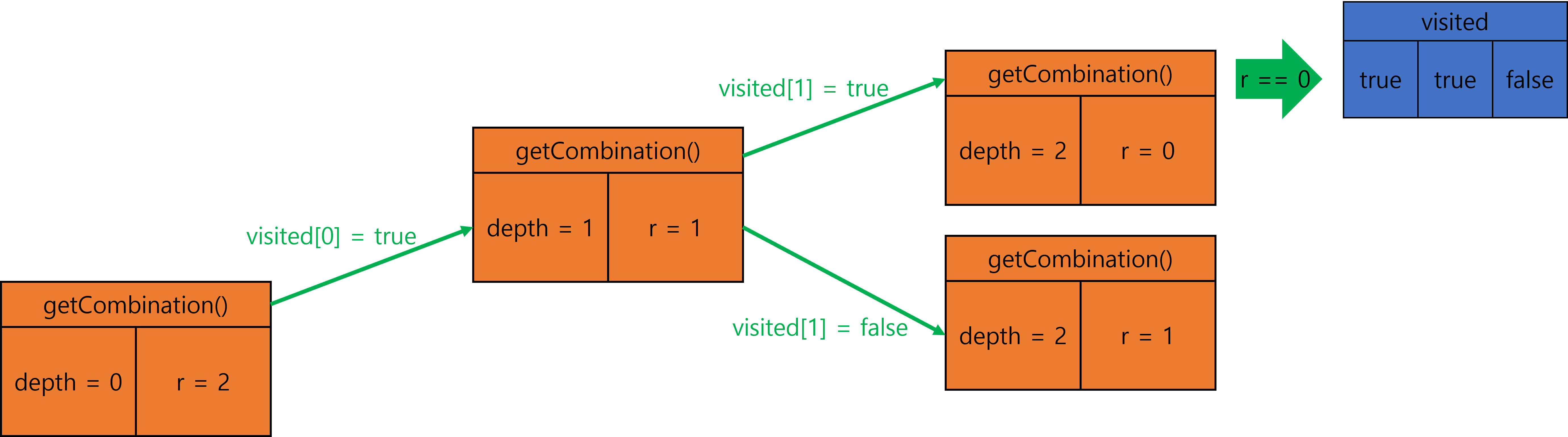
5.

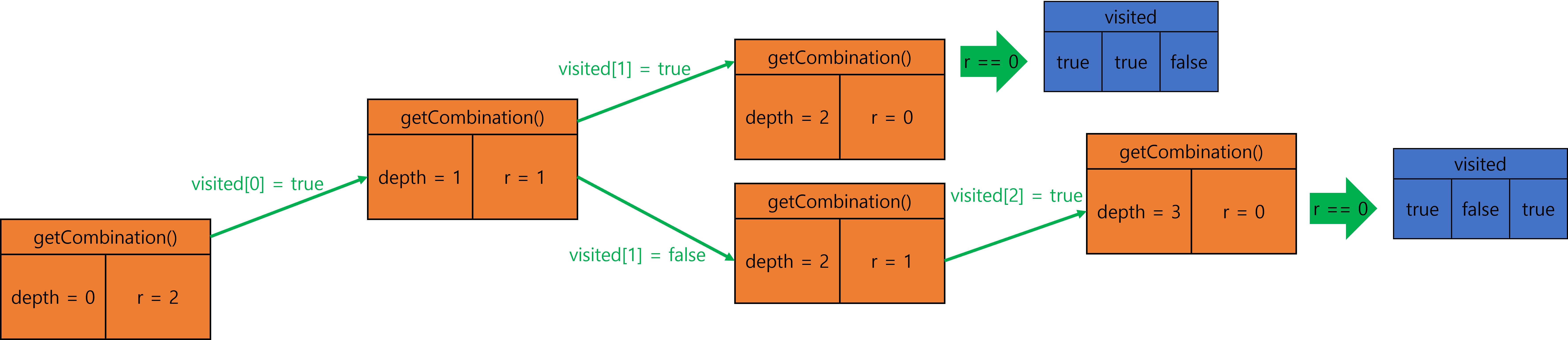
6.

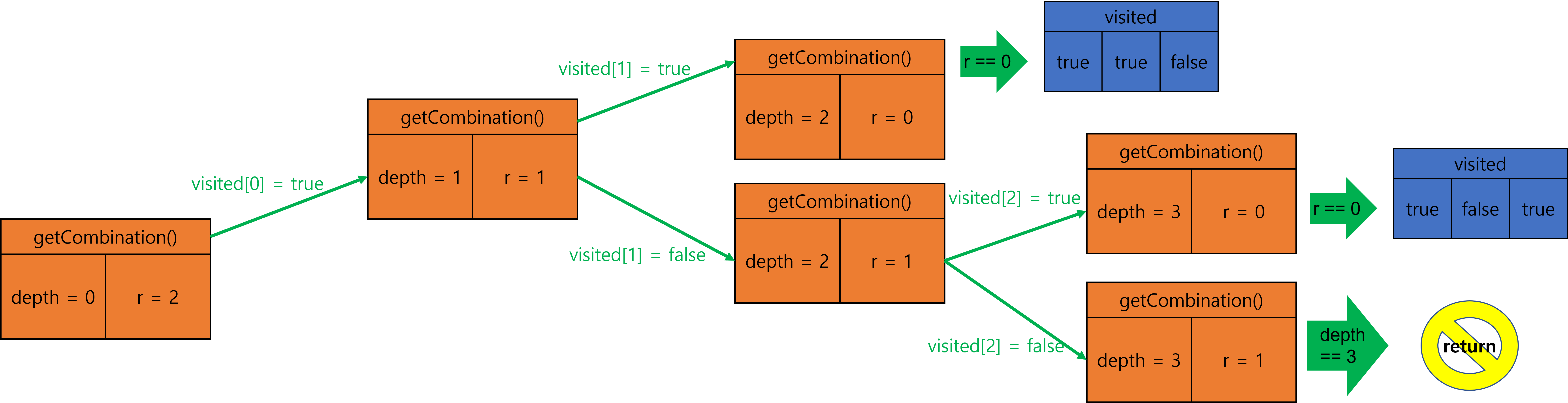
7.

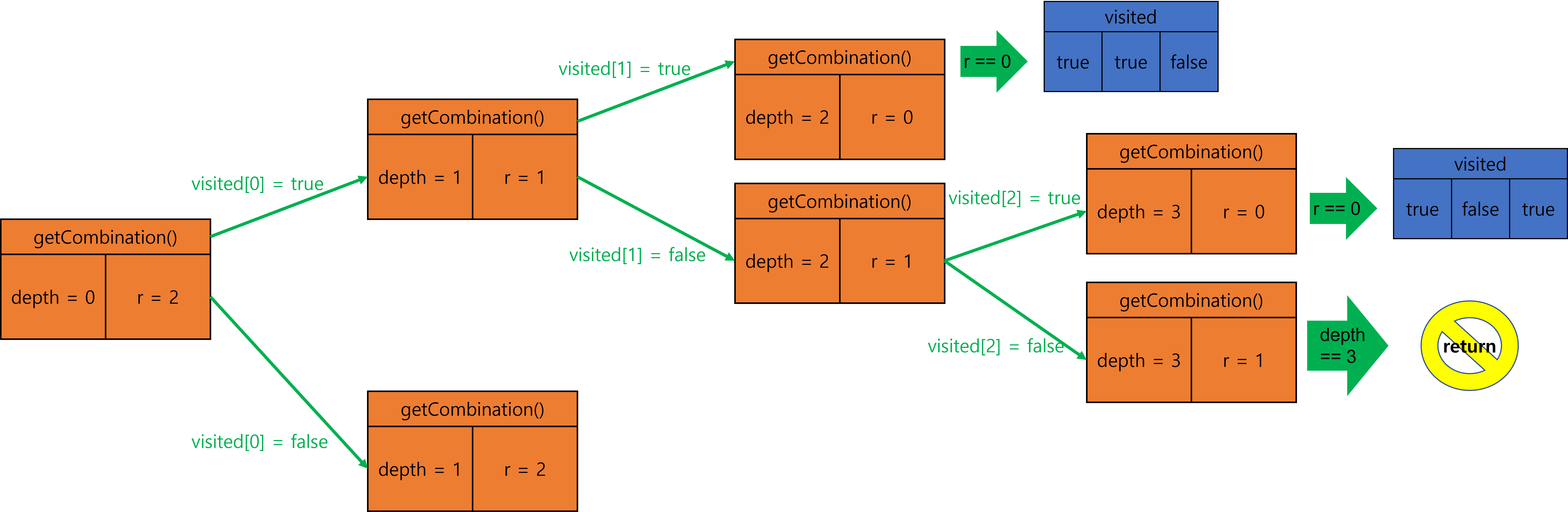
8.

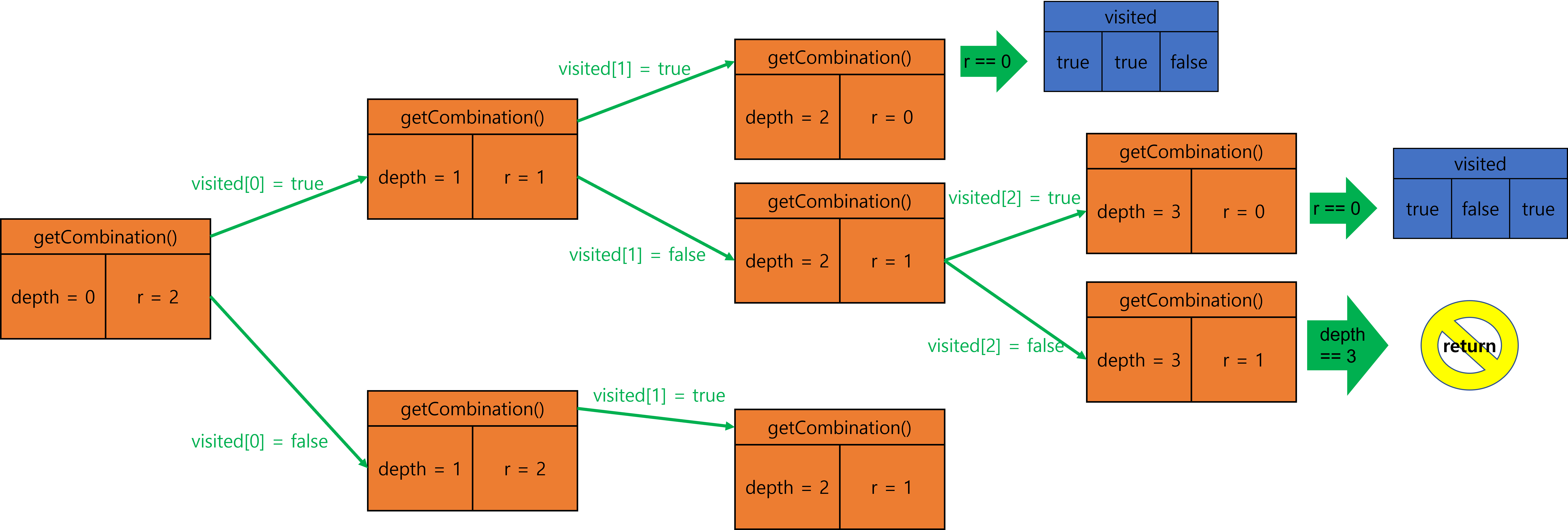
9.

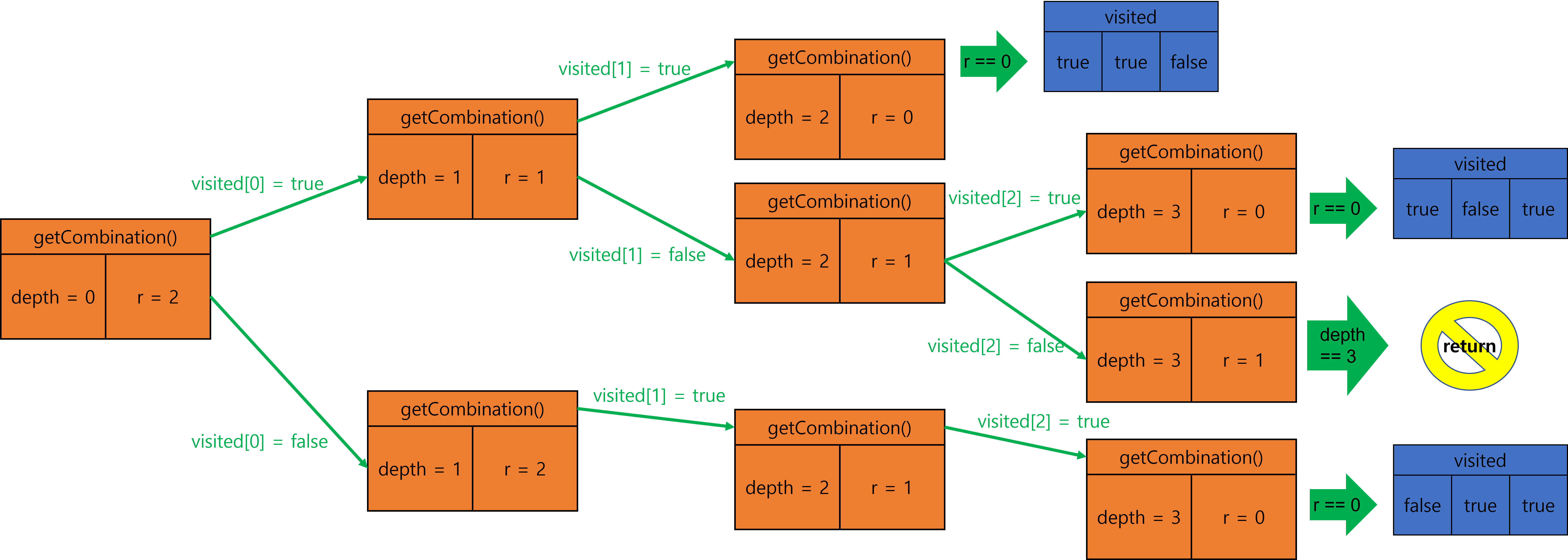
10.

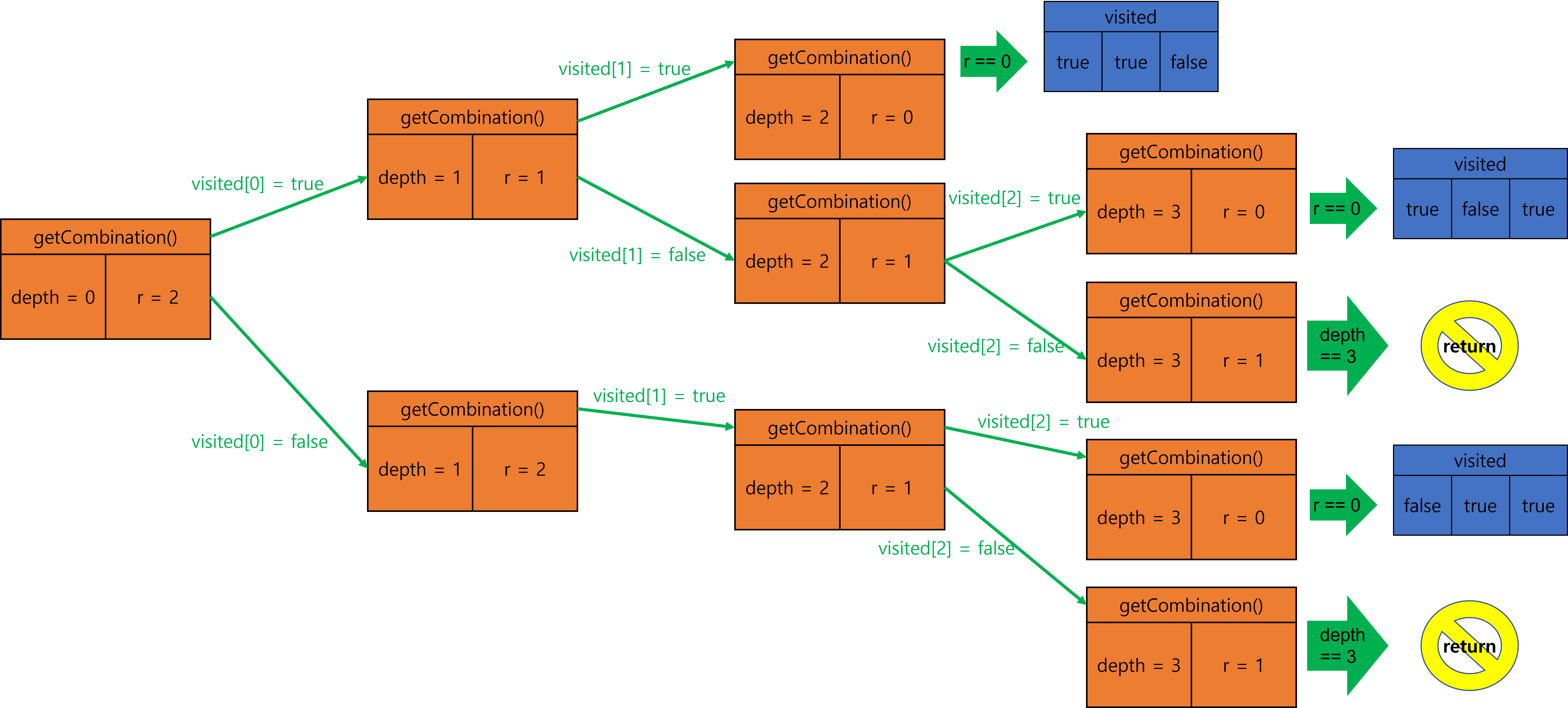
이하 생략…


중복 가능한 조합 구하기

코드

public class 중복_조합 {
  static int[] numbers = new int[] {1, 2, 3};
  static int r = 3;
  static int[] result = new int[3];

  //3개의 원소 중, 순서를 고려하지 않고 중복해서 3개를 뽑기
  public static void combination(int depth, int r, int start) { //n은 필요없다.
    if (r == 0) { //3개를 모두 뽑았다면
      printResult();
      return;
    }

    for (int i = start; i < numbers.length; i++) {
      result[depth] = numbers[i];
      combination(depth + 1, r - 1, i);
    }
  }

  private static void printResult() {
    for (int number : result) {
      System.out.print(number + " ");
    }
    System.out.println();
  }
}

상세 설명

  • visited 배열이 필요없다.
    • 중복이 가능하기 때문이다.
  • 위와는 다르게 for문을 사용하였다.