Dynamic Programming : 모든 쌍 최단 경로

개요

모든 쌍 최단 경로 문제란?

각 쌍의 점 사이의 최단 경로를 찾는 문제이다.
Ex) a에서 출발하여 b로 도착했을 때의, (a, b)의 최단경로
Ex) c에서 출발하여 f로 도착했을 때의, (c, f)의 최단경로 등..

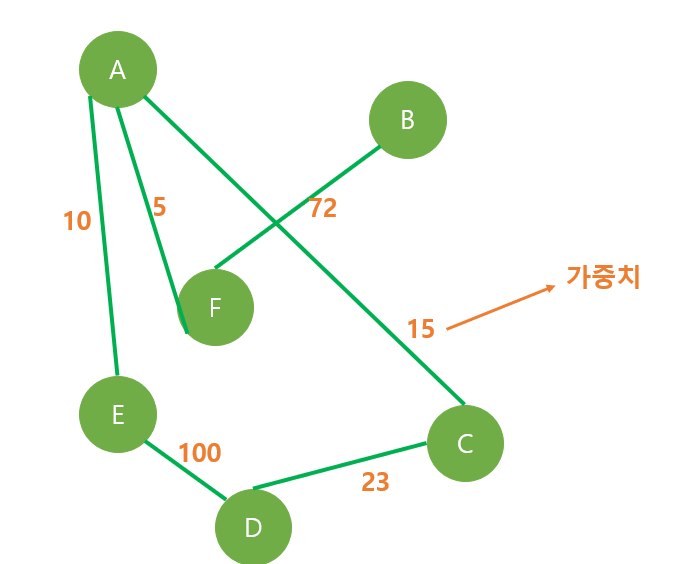
모든 쌍 최단 경로 문제란?

문제 해결 방법 - 다익스트라 알고리즘

시간복잡도

log

](https://latex.codecogs.com/svg.image?

log

)

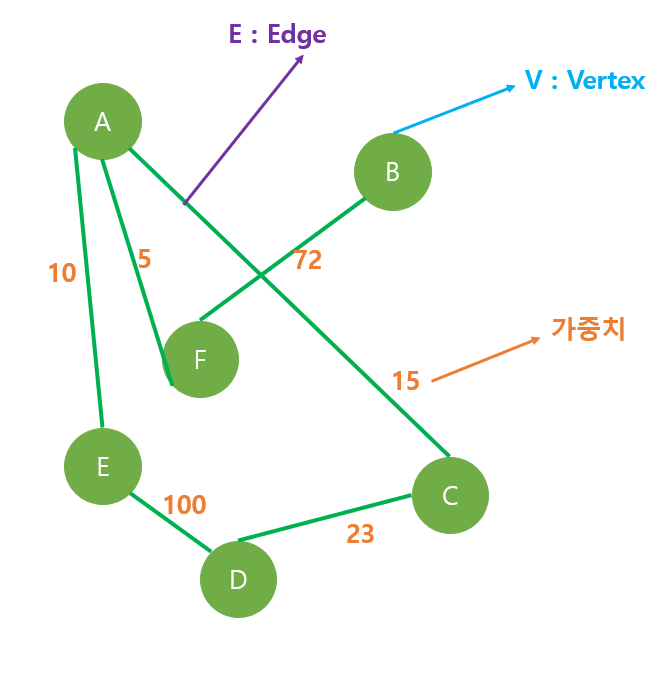
다익스트라 알고리즘

문제 해결 방법 - 플로이드 알고리즘

시간복잡도

$O(n^3)$

다익스트라 시간복잡도 : ![

log

](https://latex.codecogs.com/svg.image?

log

)

플로이드 시간복잡도 : $O(n^3)$

log

>O(n^3)](https://latex.codecogs.com/svg.image?

log

>O(n^3))

다익스트라 방식이 플로이드 방식보다 시간복잡도가 높으므로 플로이드 알고리즘을 사용하여 문제를 해결하는 것이 좋다.

부분 문제 구하기

부분문제 정의

입력 점 : 1, 2, 3, 4, … , n

- 점i에서 점j까지 갈 수 있는 모든 경로 중 가장 짧은 경로의 거리
- $D_{ij}$ : 2차원 배열
- i : 출발점
- j : 도착점
- k : i~j 까지의 최단거리에서 경유 할 수 있는 최대점
- k≠0 이더라도 경유하는 점이 없을 수 있다.
Ex) $(D_{16})^3$ 의 의미는 점1에서 출발하여, 점6에 도착하는 모든 경로에서
‘경유를 안하거나’, ‘점1을 경유하거나’, ‘점2를 경유하거나’, ‘점3을 경유할때’
중 가장 짧은 경로의 거리이다.

의 의미
- k=0 : 경유하는 점이 없다.
- 따라서, 이것은 선분 (i, j)의 기본 가중치(거리)이다.

의 의미
- 경로1 : 점i와 점j까지 한번에 가는 경로의 거리 = ${D_{ij}}^k$
- 경로2 : 점1을 경유하여 점i와 점j까지 가는 경로의 거리 = ${D_{i1}}^0+{D_{1j}}^0$
- ${D_{ij}}^1$ 의미
  - $min({D_{ij}}^k,&space;{D_{i1}}^0+{D_{1j}}^0)$

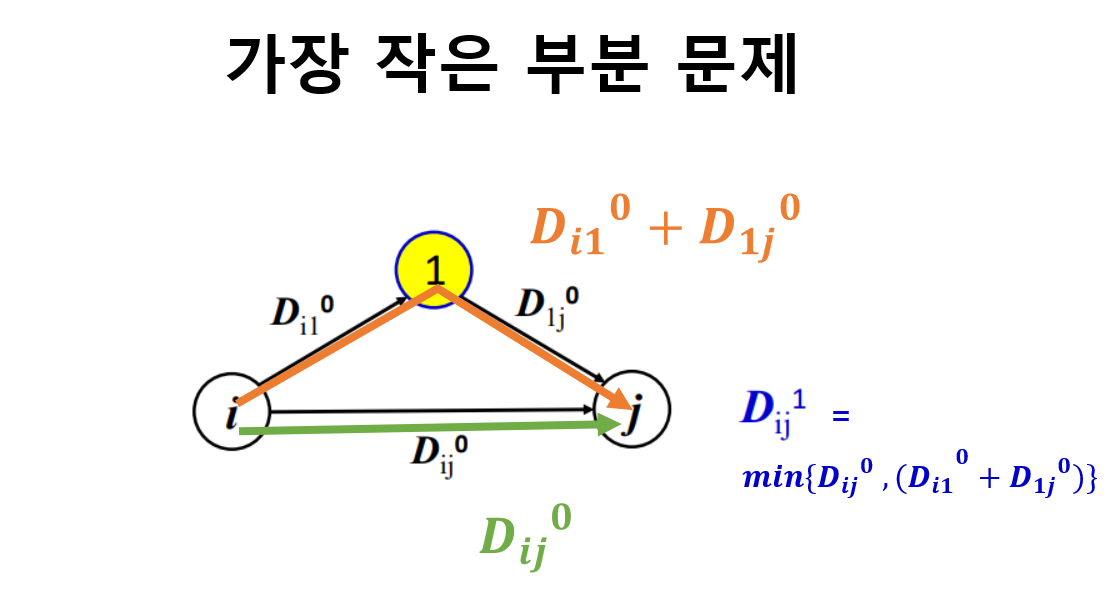
$D_{ij}^1의 의미$

즉, ${D_{ij}}^1$ 은 가장 작은 부분 문제이다.

조건
- k≠i : k는 경유를 할 수도 있는 점을 뜻하므로, “시작점≠경유점”
- k≠j : k는 경유를 할 수도 있는 점을 뜻하므로, “도착점≠경유점”
- i≠j : “시작점≠도착점”

부분 문제 원리

점의 개수가 3개 인 경우의 해 : (i, j)의 최단 경로
- 점i에서 점j로 직접가는 경우
- 점1을 경유하여 가는 경우
- 총 2가지의 경우 중, 짧은 것을 선택하면 된다.
  
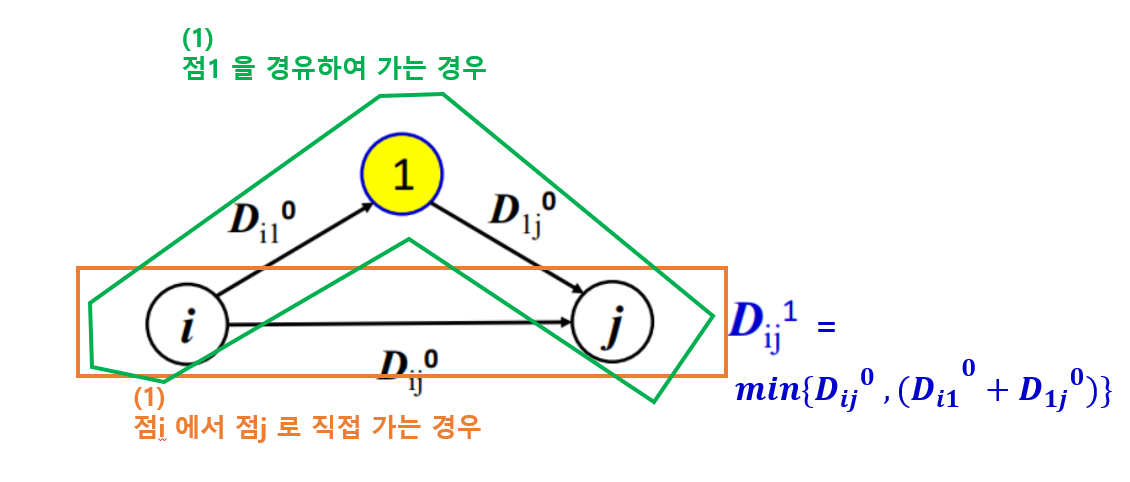
  <상향 방법 (bottom-up)>
  점1 로부터 시작하여, 점2, 점3, 점4, … , 점n 까지 모든 점을 경유 가능한 점들로 고려하면서, 모든 쌍의 최단 경로의 거리를 계산한다.

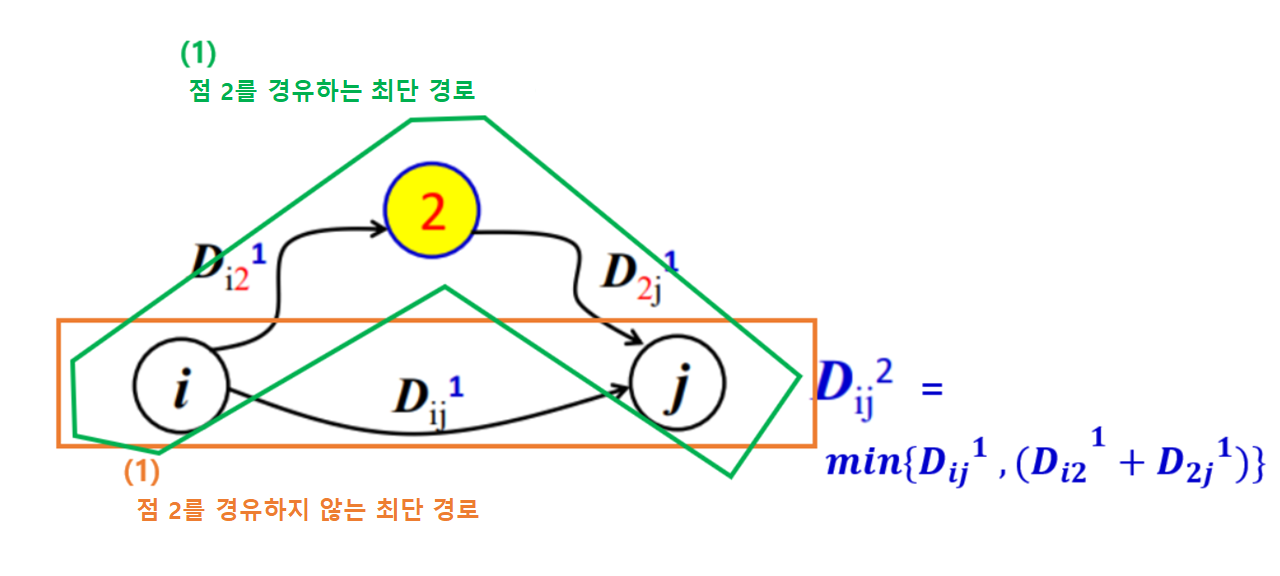
점의 개수가 4개 인 경우의 해 : (i, j)의 최단 경로
- ‘점i에서 점j로 직접가는 경우’
- ‘점2을 경유하여 가는 경우’
- 총 2가지의 경우 중, 짧은 것을 선택하면 된다.

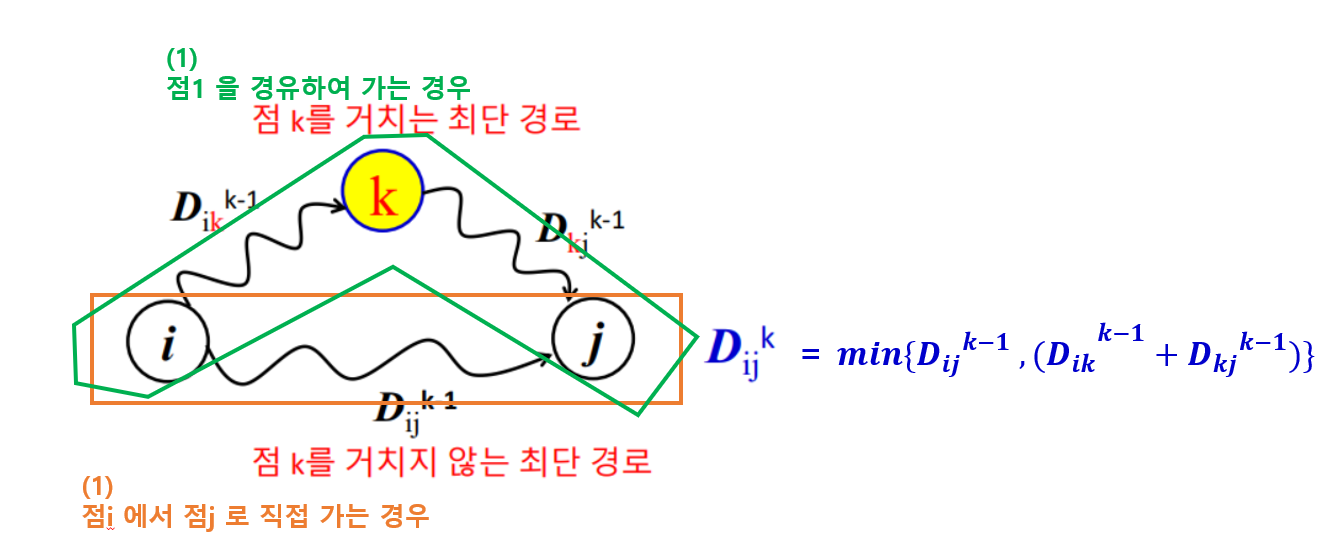
점의 개수가 k개 인 경우의 해 : (i, j)의 최단 경로
- ‘점i에서 점j로 직접가는 경우’
- ‘점k을 경유하여 가는 경우’
- 총 2가지의 경우 중, 짧은 것을 선택하면 됨
정리
- 즉, ${D_{ij}}^k=min({D_{ij}}^{k-1},&space;({D_{ik}}^{k-1}+{D_{kj}}^{k-1}))$

알고리즘

의사코드

단, 경로를 만드는 것이 불가능한 점간의 거리는 무한대이다.

절차 : 1번 라인

k : 경유할 수도 있는 점들의 개수
k를 점차 늘려간다.
- 왜냐하면 경유할 수 있는 모든 점들에 대해 결과를 구해야하기 때문이다.

절차 : 2번 라인

i : 시작점
i를 점차 늘려간다.
- 왜냐하면 점들의 가능한 모든 경로를 구해야 하기 때문이다.

절차 : 3번 라인

j : 도착점
j를 점차 늘려간다.
- 왜냐하면 각 출발점마다 모든 도착점에 대한 경로를 구해야 하기 때문이다.

절차 : 4번 라인

${D_{ij}}^k=min({D_{ij}}^{k-1},&space;({D_{ik}}^{k-1}+{D_{kj}}^{k-1}))$
위와 같은 부분문제 공식을 적용한다.

주의사항

선분들의 가중치 합이 음수가 되는 것이 없어야 한다.
이것을 음수 사이클이라고 한다.

수행 예시

입력

초기값
- 배열 D에는 각 점들간의 기본가중치 값이 들어있다.

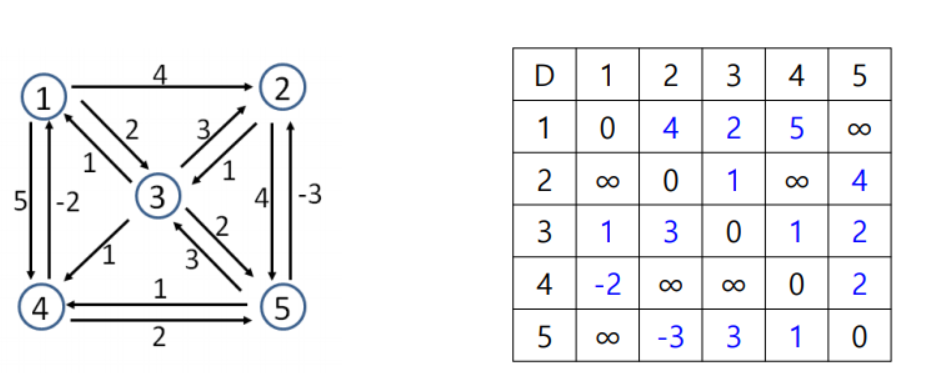
수행 예시 (입력)

k=1 일 경우

$D[2][3]=min(D[2][3],D[2][1]+D[1][3])=min(1,\infty)=1$
$D[2][4] = min(D[2][4],D[2][1]+D[1][4])=min(∞,∞)=∞$
$D[2][5] = min(D[2][5],D[2][1]+D[1][5])=min(4,∞)=4$
…..
$D[4][2] = min(D[4][2],D[4][1]+D[1][2])=min(∞,2)=2$ 이때, 배열이 갱신된다.

경유하는 경로가 더 짧을 때, 배열의 값이 갱신된다.
…..
$D[5][4] = min(D[5][4],D[5][1]+D[1][4])=min(1,∞)=1$