동적 계획 : 연속 행렬 곱셈

개요

연속 행렬 곱셈이란?

• 연속된 행렬들의 곱셈에 필요한 원소간의 최소 곱셈 횟수를 찾는 문제

행렬곱이란

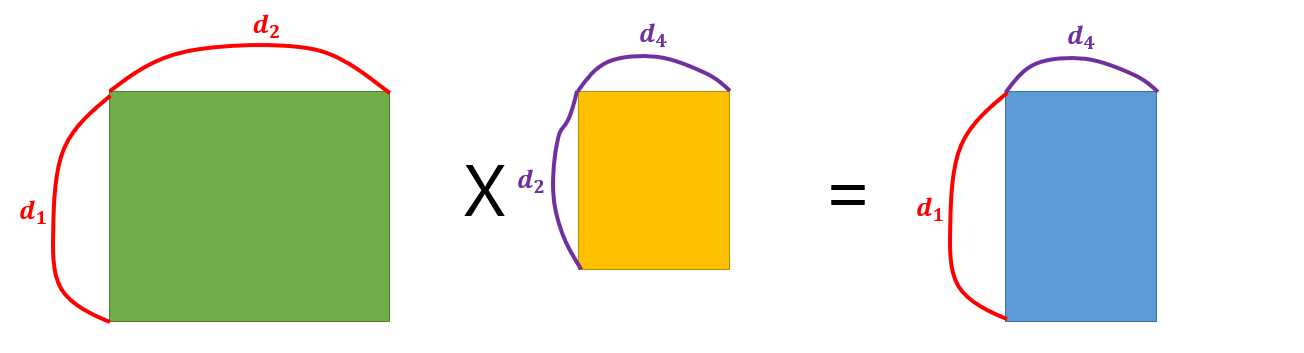
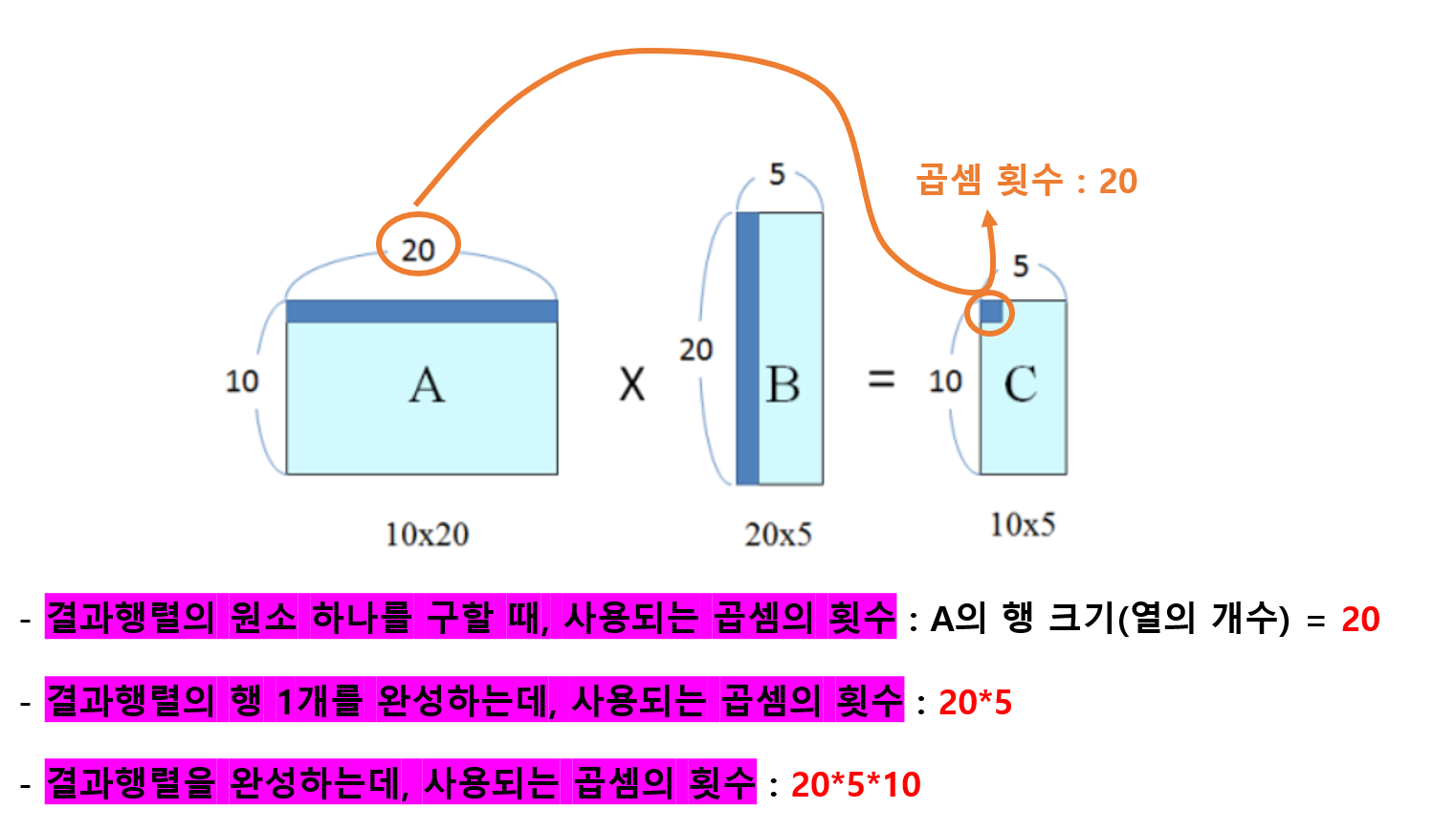
곱셈횟수

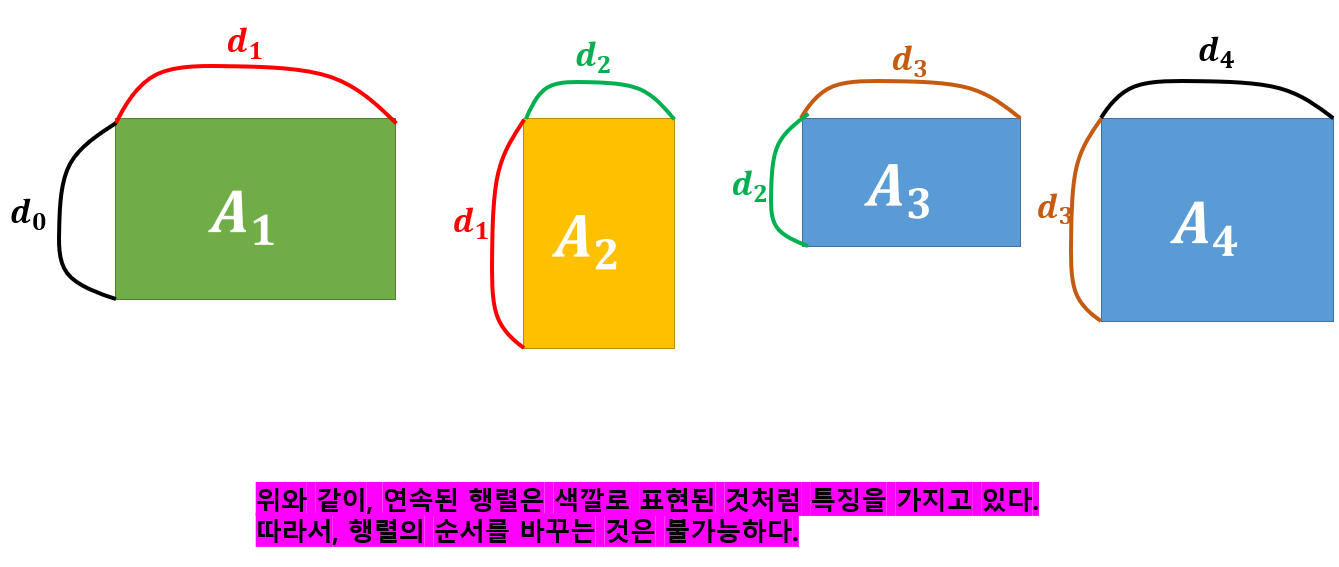
연속된 행렬

문제배경

• 연속된 행렬이 3개 이상일때, 결합법칙이 성립된다.

• 행렬들의 곱셈 순서에 따라, 최종 곱셈 횟수가 달라진다.

• ex) 일때
  • 
  • 
  • 위와 같이 2가지의 경우의 수가 가능하다.
  • 단, 와 같이 행렬의 순서 자체를 바꾸는 것은 불가능하다.

알고리즘

최적화 원리

• 최적의 곱셈 순서를 A_4)A_5)A_6)) 이라고 가정하자.
• 이때, 은 반드시 연속된 행렬 의 최적의 곱셈 순서이다.
• 즉, 작은 문제의 해가 큰 문제의 해에 포함된다. ⇒ 다이나믹 프로그래밍

의사코드

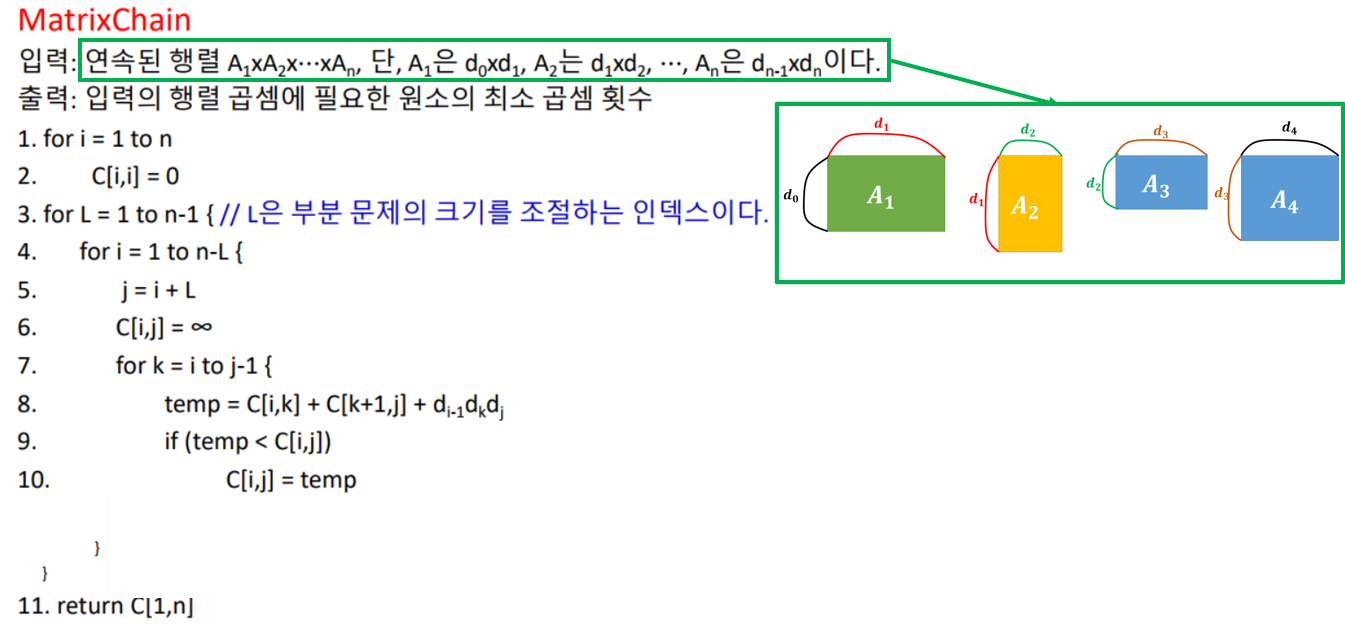
• 행렬
  • 
• C[i][j]
  • 까지의 최소 곱셈 횟수
• C[i][j] 구하는 식
  • 
• 참고
  • k는 C[i][j]를 구하기 위해 연속된 행렬들이 2개로 나눠지는데, k가 바로 이때의 기준 행렬의 번호이다.

C[i][j] 계산 방법

• C[1][2] 일때 (행렬의 개수가 2개일 때)

  • 

    

• C[1][3] 일때 (행렬의 개수가 3개일 때)

  • 

  • 의 최소곱셈개수 =

    

  • 의 최소곱셈개수 =

    

동작 예시

절차 : 1~2번 라인

• 배열의 대각선 원소들인 을 0으로 초기화 시킨다.
• 왜냐하면  과 같은 행렬끼리는 (즉, 자기자신끼리는) 계산할 필요가 없기 때문이다.

절차 : 3번 라인

• L의 크기에 따라, 배열C가 점차 채워진다.

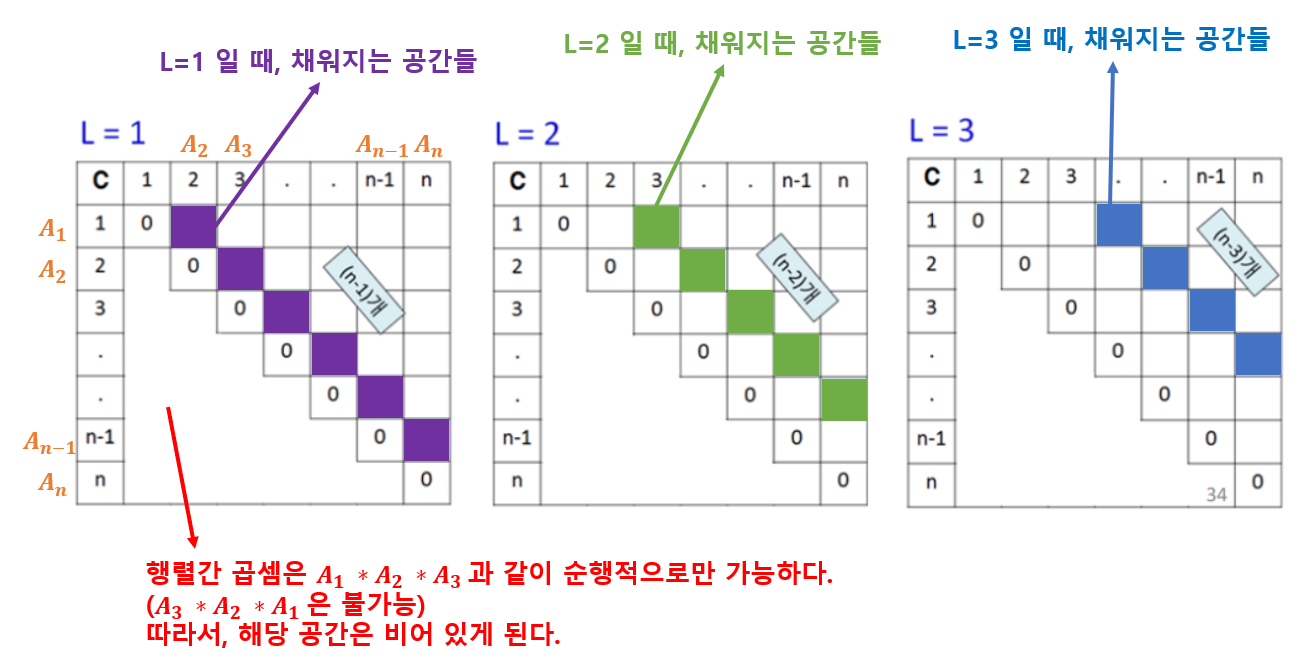
절차 : 5번 라인

• j=i+L 은 C[i][j]를 계산하기 위한 것

절차 : 6번 라인

• 최소 곱셈 횟수를 찾기 위해 C[i][j]로 초기화시킨다.

절차 : 7~10번 라인

• k값을 i ~ (j-1) 까지 변화시킴
• k값을 변화시키며, C[i][j]를 찾음

---

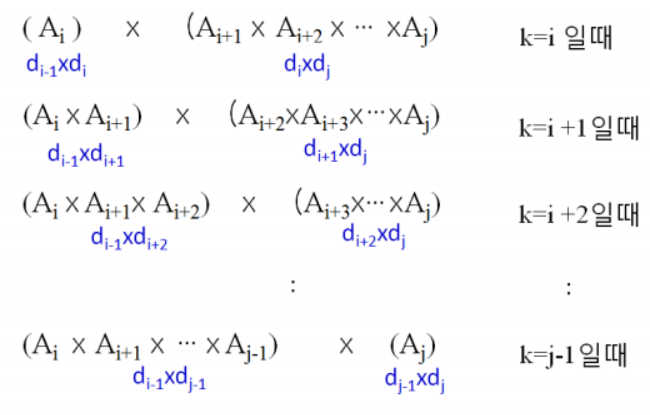
• 성결대학교 컴퓨터 공학과 임태수 교수님 (2021)
• 양성봉, 『알기 쉬운 알고리즘』

본 게시글은 위 강의 및 교재를 기반으로 정리한 글입니다.