바닥 공사
문제
문제 정의
- 가로의 길이가 N, 세로의 길이가 2인 직사각형 형태의 얇은 바닥이 있다.
- 태일이는 이 얇은 바닥을 1x2의 덮개, 2x1의 덮개, 2x2의 덮개를 이용해 채우고자 한다.
-
바닥: Nx2
회색 영역은 무시하자.
-
1x2 덮개
-
2x1 덮개
-
2x2 덮개
-
- 이때 바닥을 채우는 모든 경우의 수를 구하는 프로그램을 작성하시오.
- 예시
- 2x3 크기의 바닥을 채우는 경우의 수는 5가지이다.
입력조건
- 첫째 줄에 정수 N이 주어진다.
- N: 1 이상, 1,000 이하
출력조건
- 첫째 줄에 2xN 크기의 바닥을 채우는 방법의 수를 796,796으로 나눈 나머지를 출력한다.
입·출력 예시
- 입력
3 - 출력
5
풀이
문제 해설
- 문제 풀이를 위해 도식화해보자.
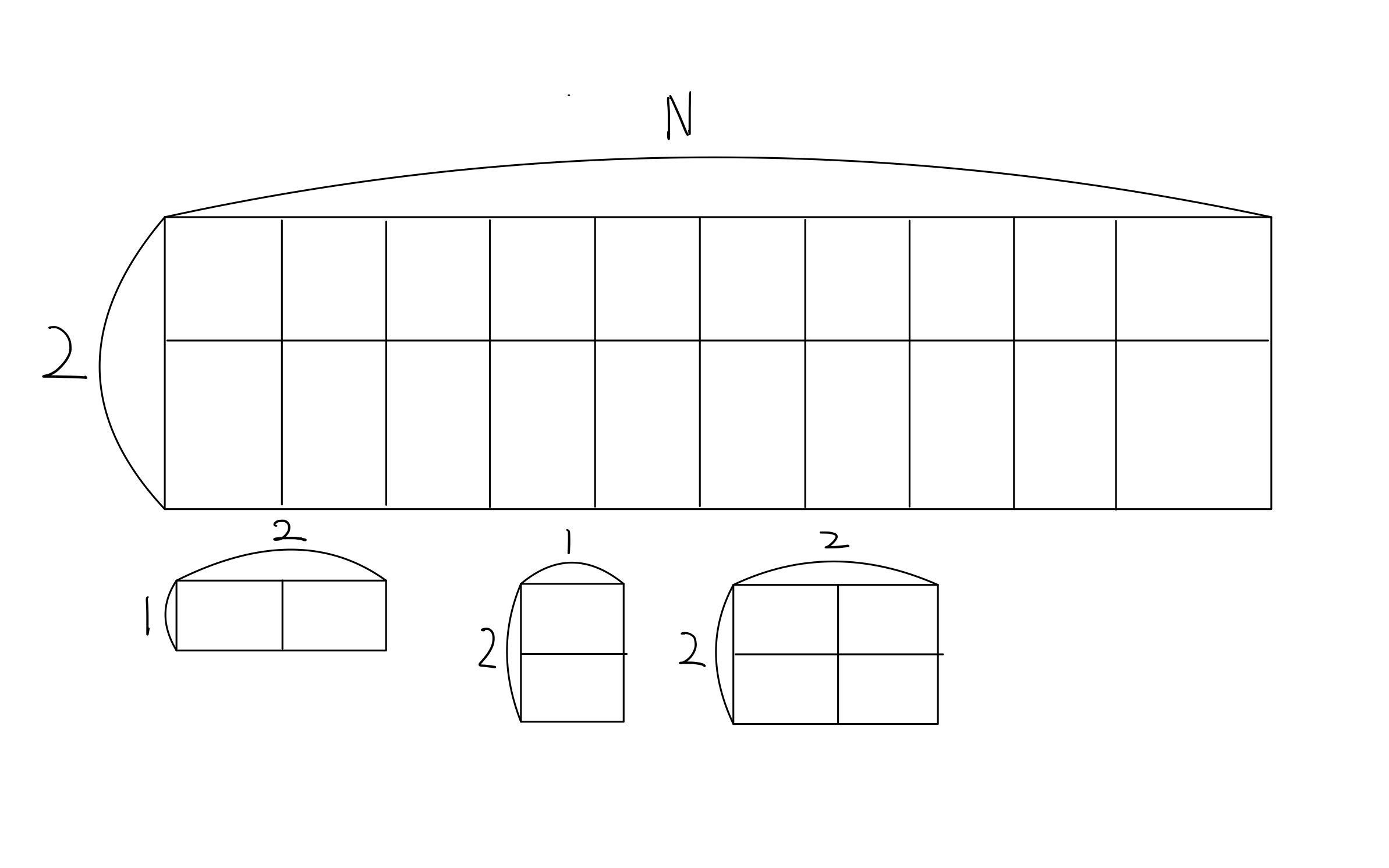
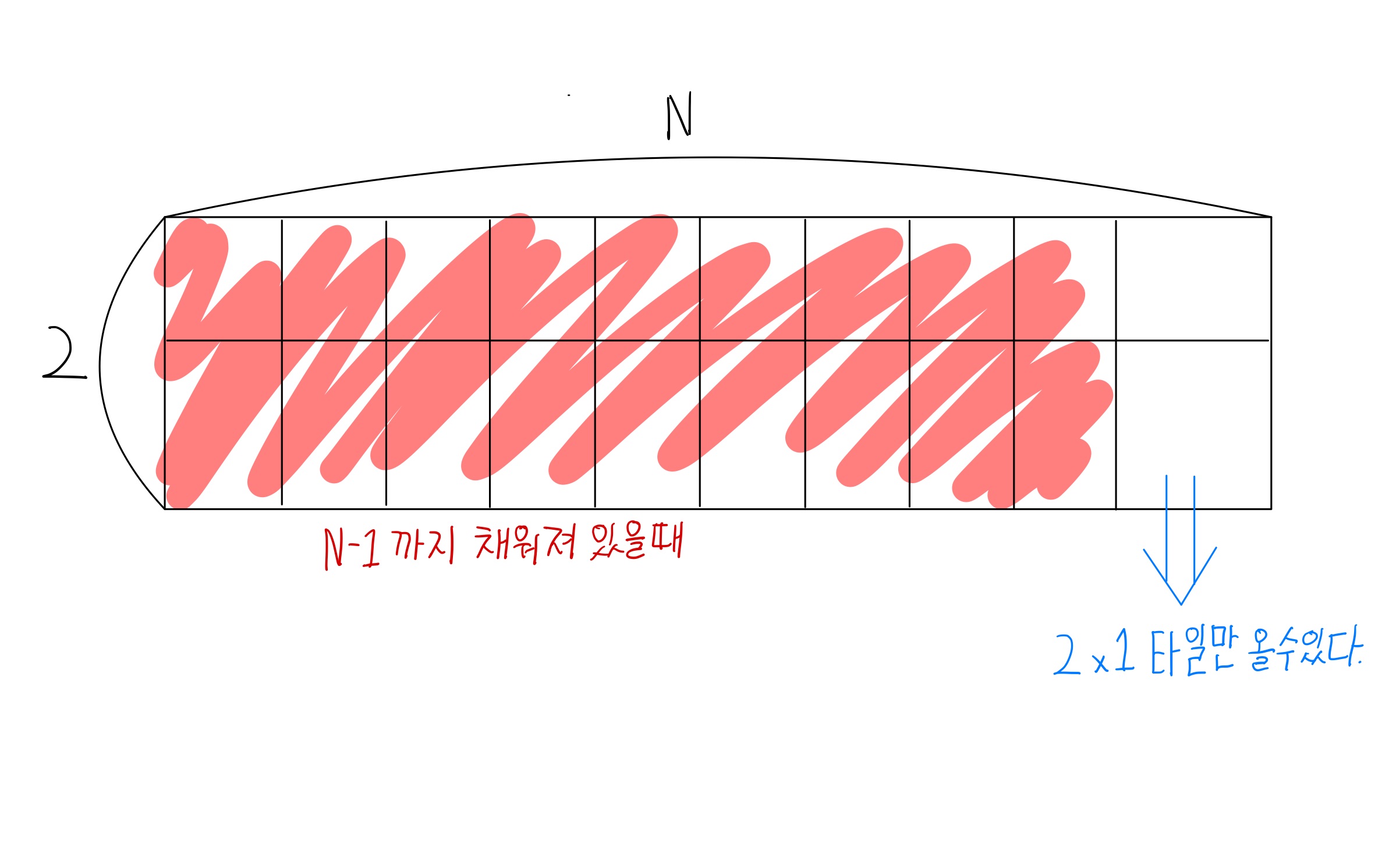
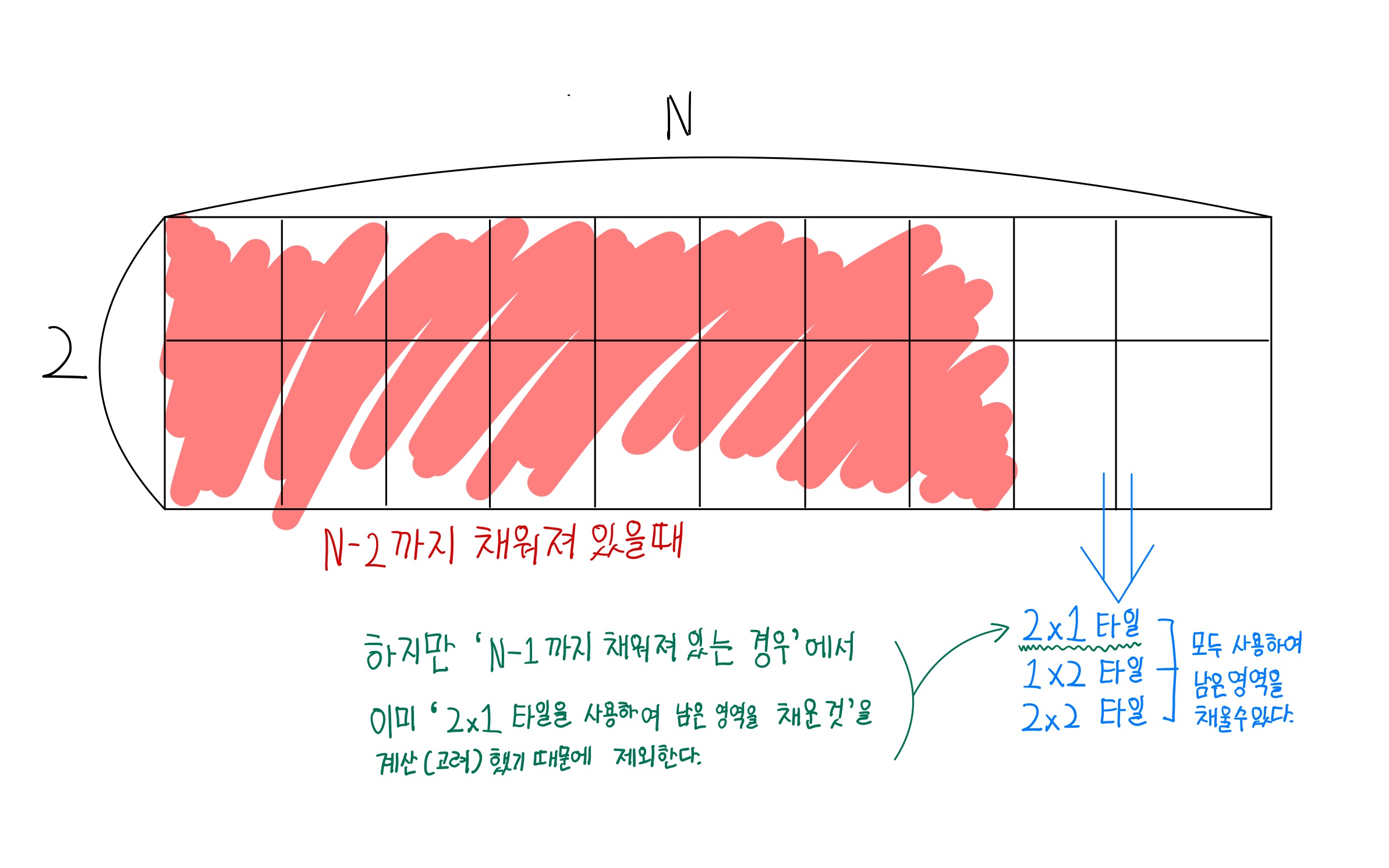
- 이것을 점화식으로 표현하면 아래와 같다.
: ix2 영역을 채우는 모든 경우의 수
소스코드
public class 바닥_공사 {
static int[] d = new int[1000];
private static int solution1(int n) {
//d[n] = n*2의 영역을 채우는 경우의 수
d[0] = 0;
d[1] = 1;
d[2] = 3;
for (int i = 3; i <= n; i++) {
d[i] = (d[i-1] + 2*d[i-2])%796796;
}
return d[n];
}
public static void execute() throws Exception {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(bf.readLine());
TimeCheck.start();
int answer = solution1(n);
TimeCheck.end();
System.out.println(answer);
}
}
- 나동빈, 『이것이 코딩 테스트다』
