퀵정렬
개요
퀵정렬이란?
- 기준 데이터를 설정하고 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾸어나가며 정렬하는 알고리즘이다.
- 기준을 설정한 다음 큰 수와 작은 수를 교환한 후, 리스트를 반으로 나누는 방식으로 동작한다.
- 피벗(pivot): 큰 숫자와 작은 숫자를 교환할 때, 교환하기 위한 ‘기준’ 을 피벗이라고 한다.
- 피벗 선정의 기준에는 여러가지가 있으나, 여기서는 가장 앞에 있는 숫자를 피벗으로 삼는
호어분할방식을 사용한다. - 재귀함수를 통해 구현할 수 있다.
퀵정렬 동작 과정
- 가장 앞의 숫자를 피벗으로 선정한다.
- 피벗을 제외한 가장 앞의 숫자부터 ‘피벗보다 큰 숫자가 존재하는지’ 찾는다.
- 가장 뒤의 숫자부터 ‘피벗보다 작은 숫자가 존재하는지’ 찾는다.
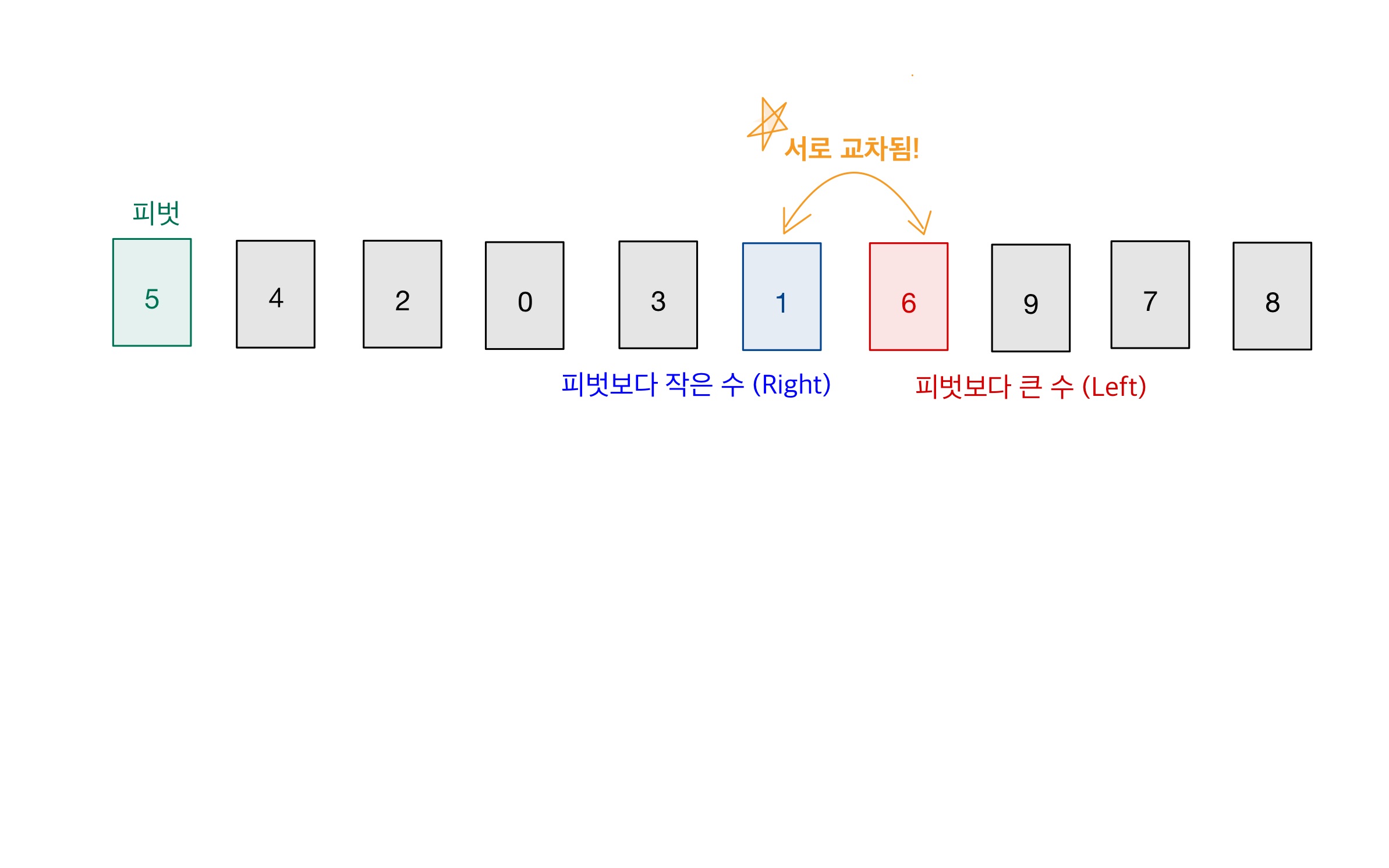
- ‘2번에서 찾은 숫자’가 ‘3번에서 찾은 숫자’ 보다 앞에 있다면,
‘2번’과 ‘3번’에서 찾은 숫자를 서로 교환한다. (위치를 바꾼다.)
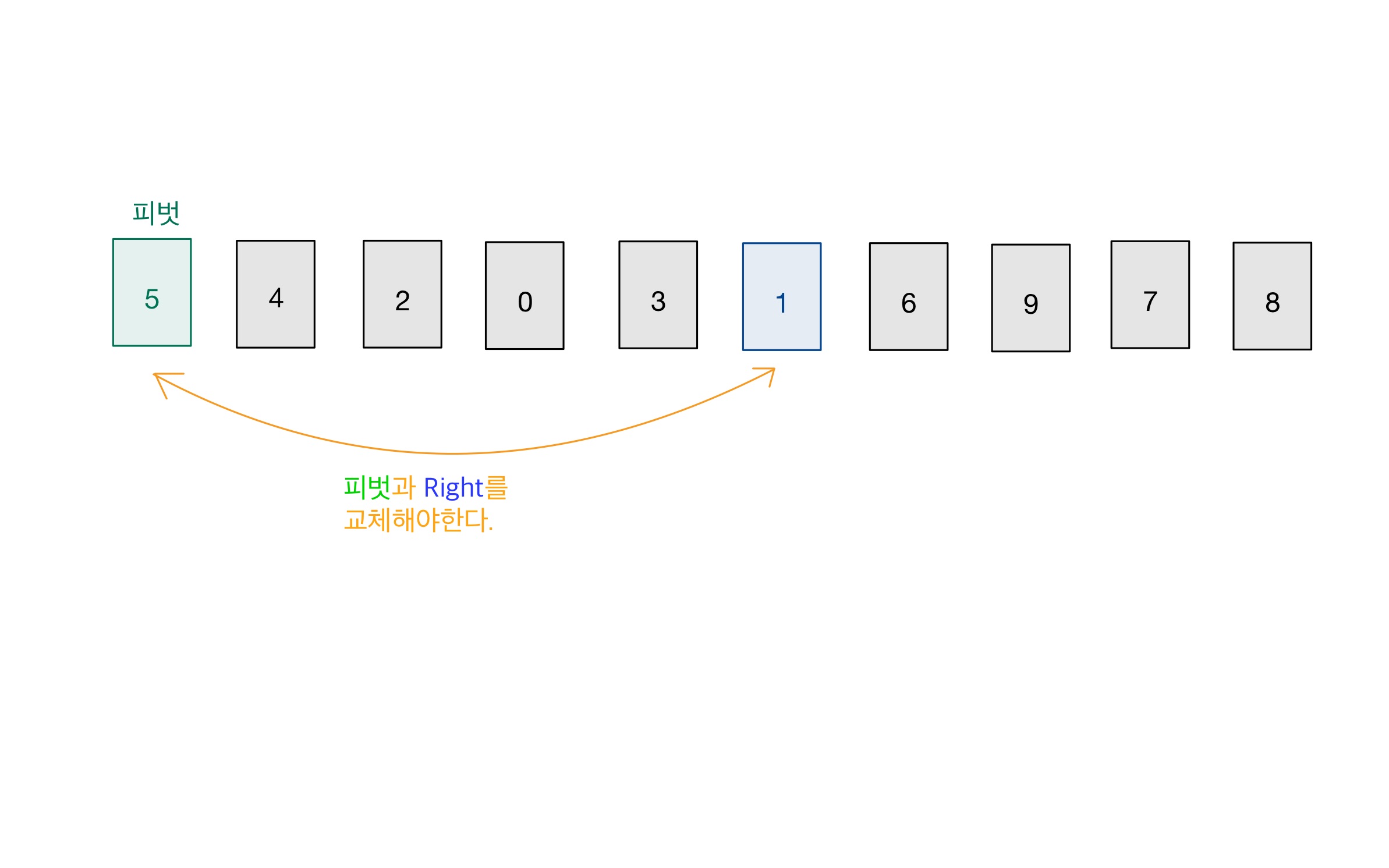
그리고 2번으로 돌아간다. - ‘2번에서 찾은 숫자’가 ‘3번에서 찾은 숫자’ 보다 뒤에 있다면,
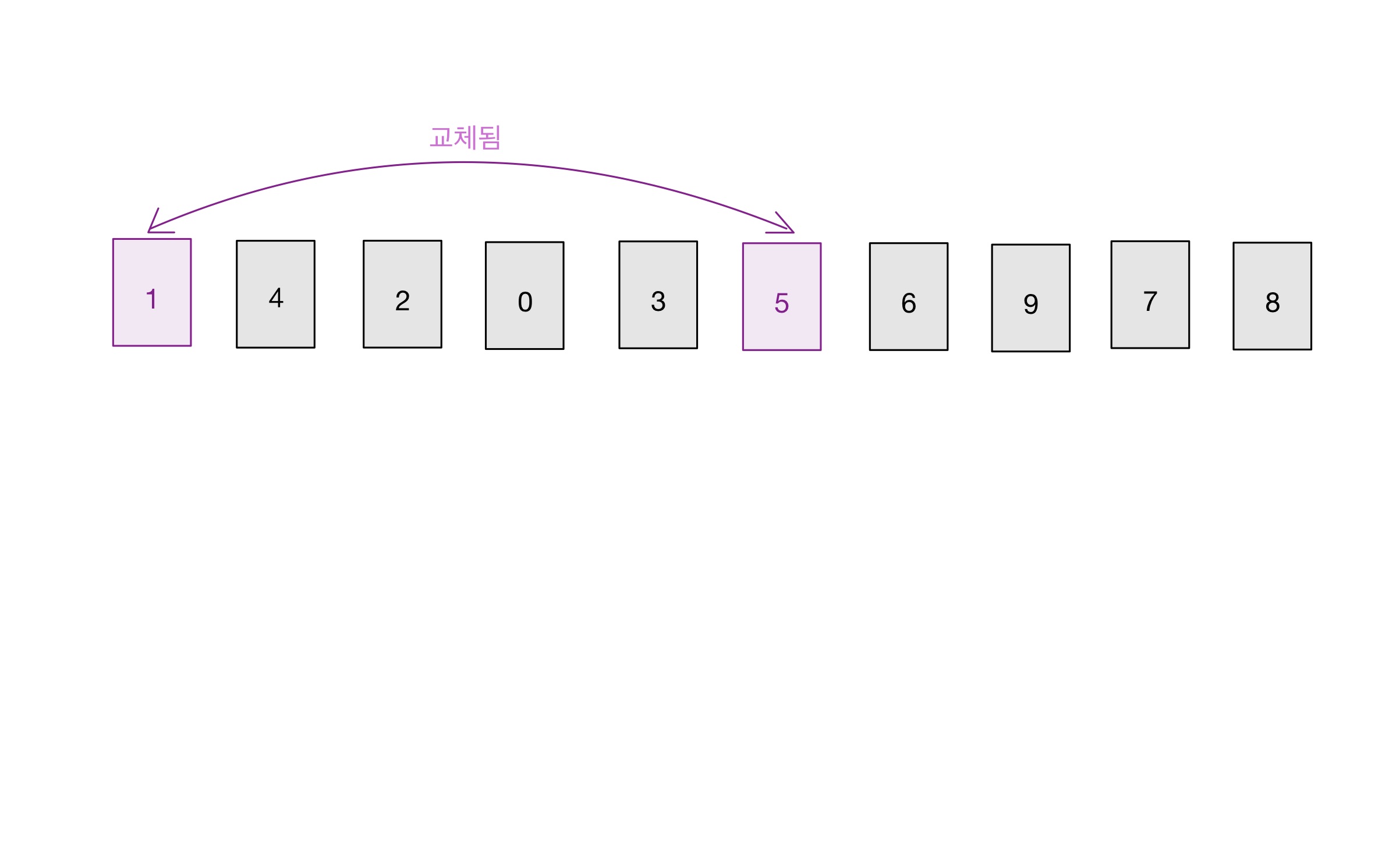
‘3번’에서 찾은 숫자와 ‘피벗’을 서로 교환한다. (‘피벗보다 작은 수’와 ‘피벗’ 위치를 바꾼다.)
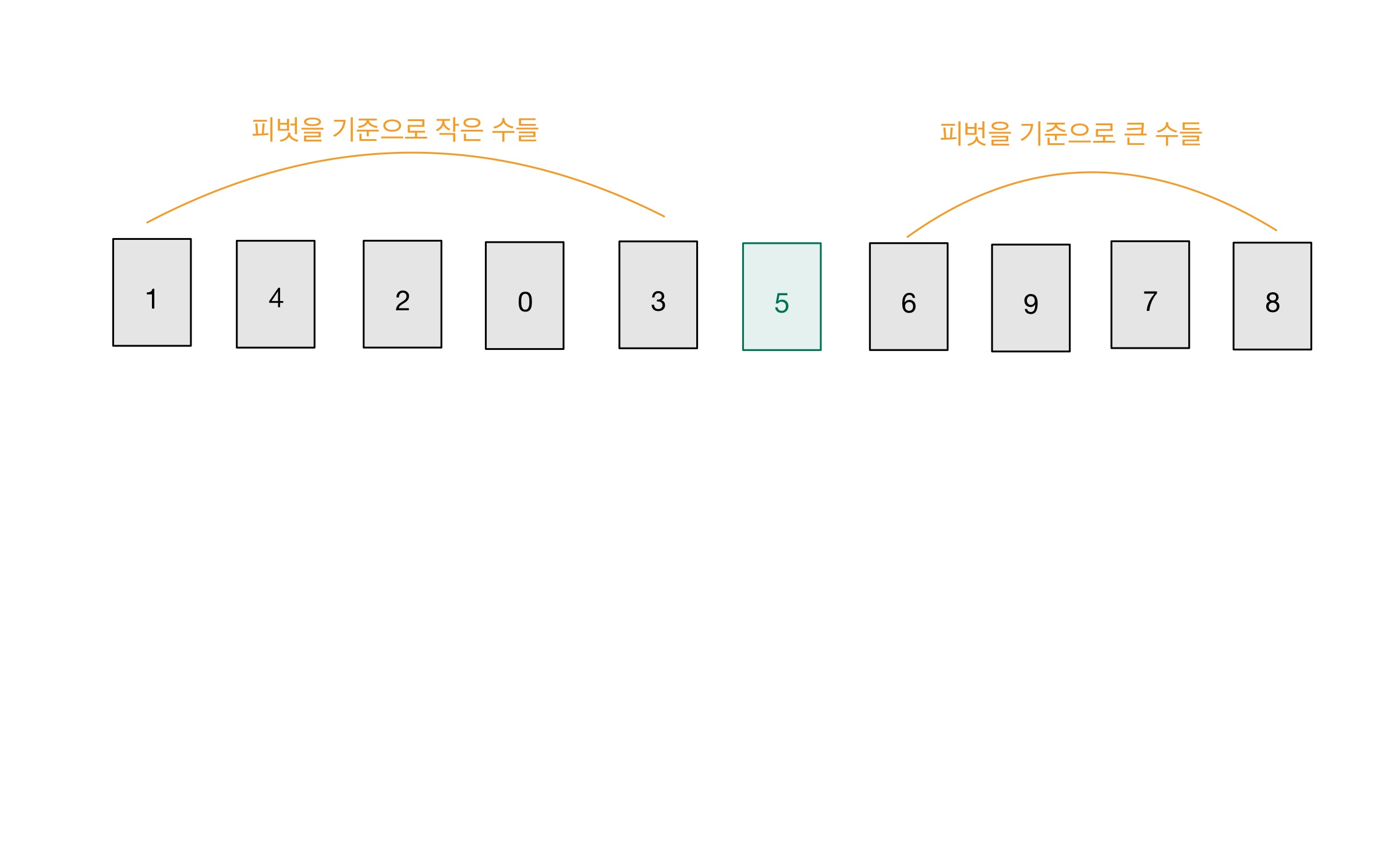
그리고 6번을 수행한다. - ‘가장 앞의 숫자(피벗과 교환된 숫자)’부터 ‘피벗과 교환된 숫자의 바로 앞 숫자’ 까지 하나의 수열로 취급한다.
그리고 ‘피벗과 교환된 숫자의 바로 뒤 숫자’부터 ‘가장 뒤의 숫자’까지 하나의 수열로 취급한다.
이때 각 수열의 원소가 2개 이상이라면, 각각 다시 1번부터 수행한다.
(재귀)
예시
예시에서 사용할 배열 형태
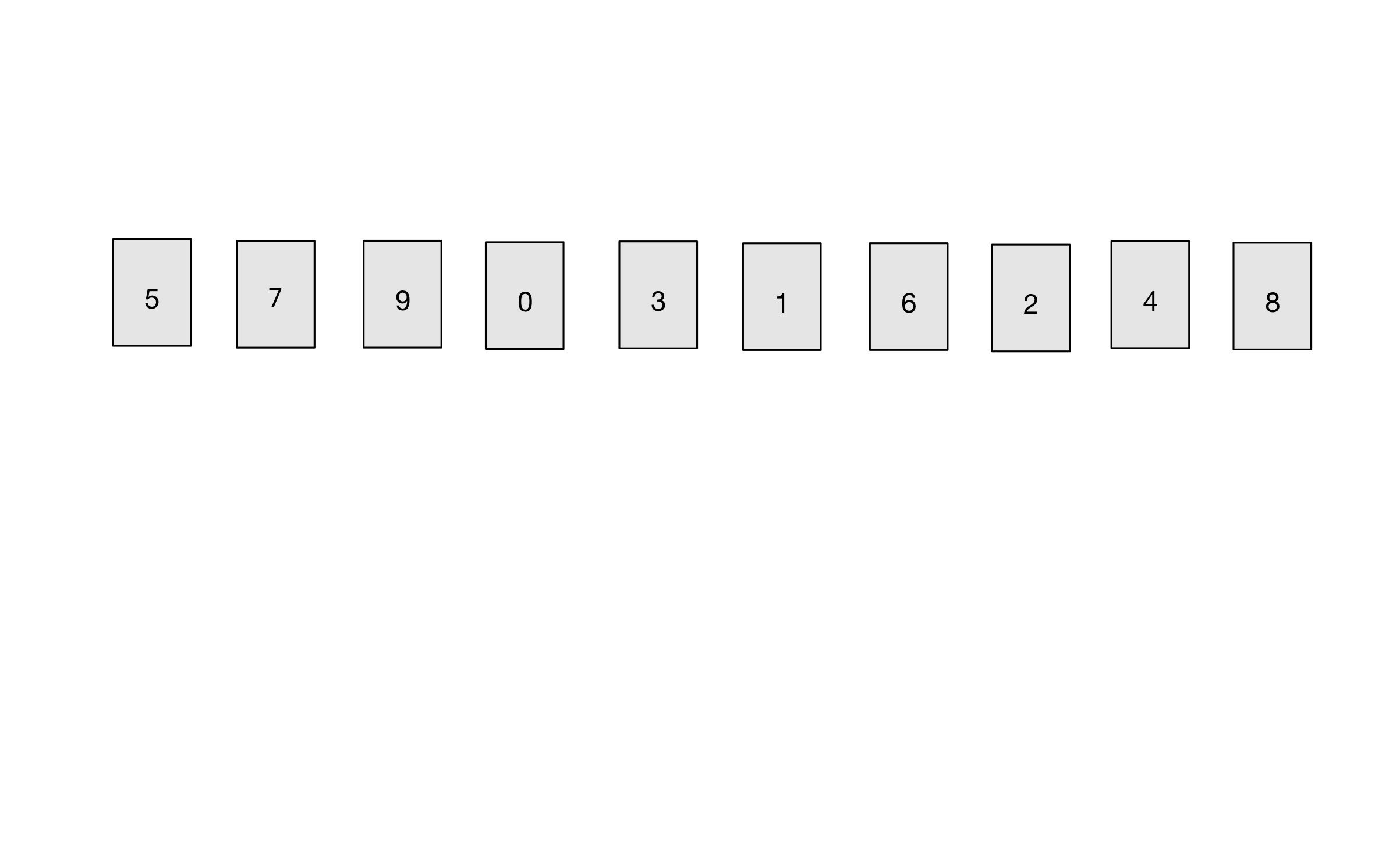
Step 01
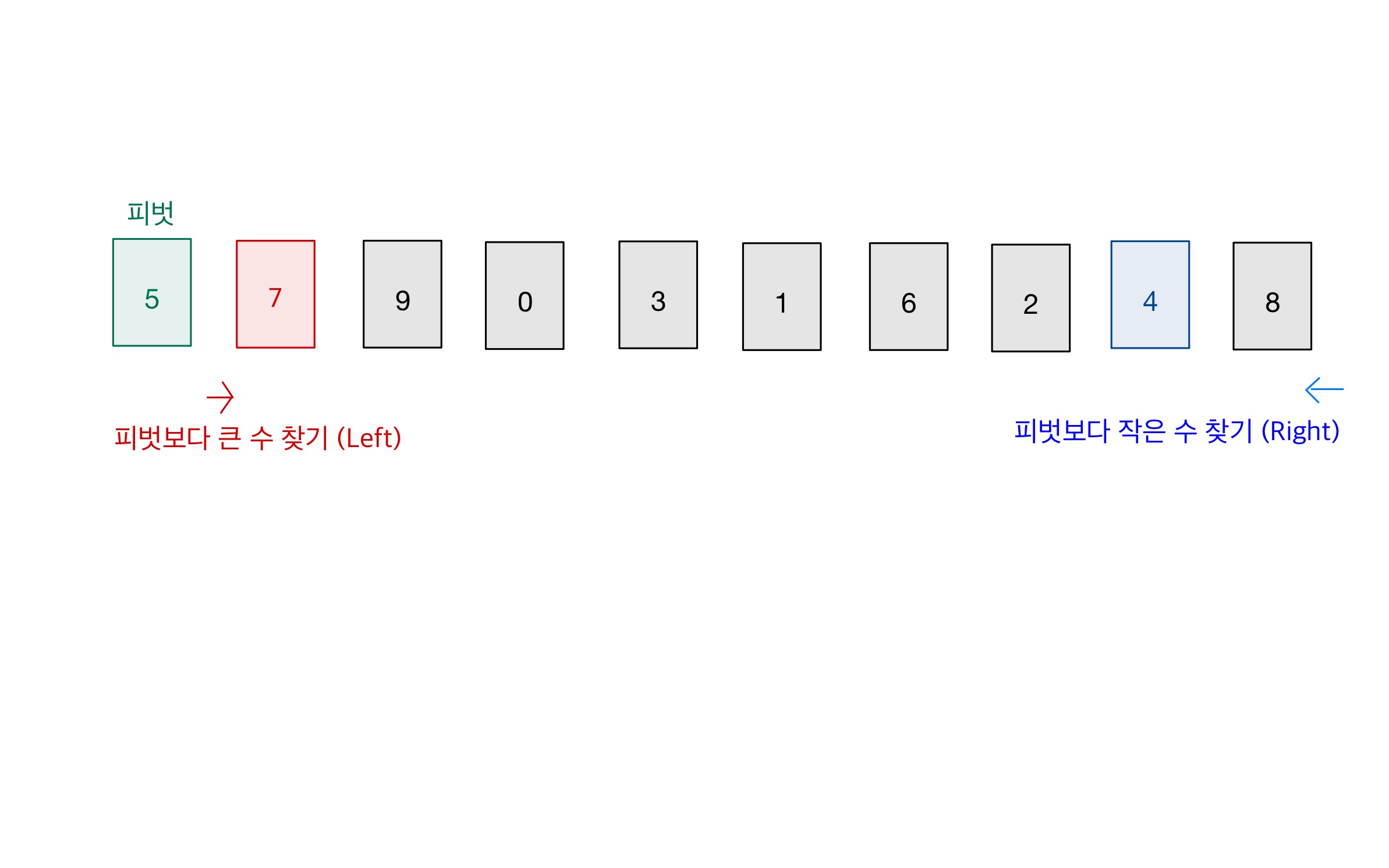
Step 02
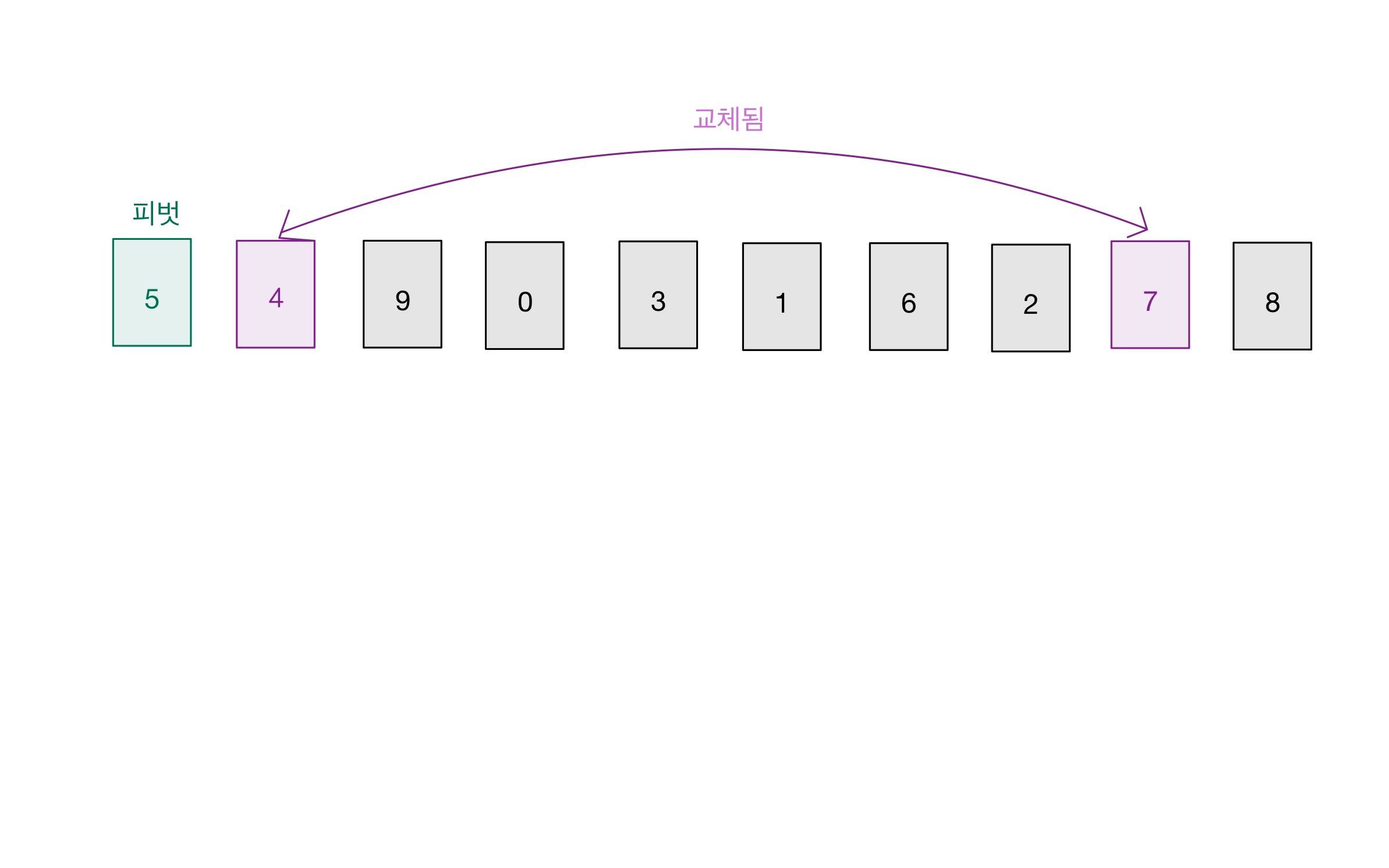
Step 03
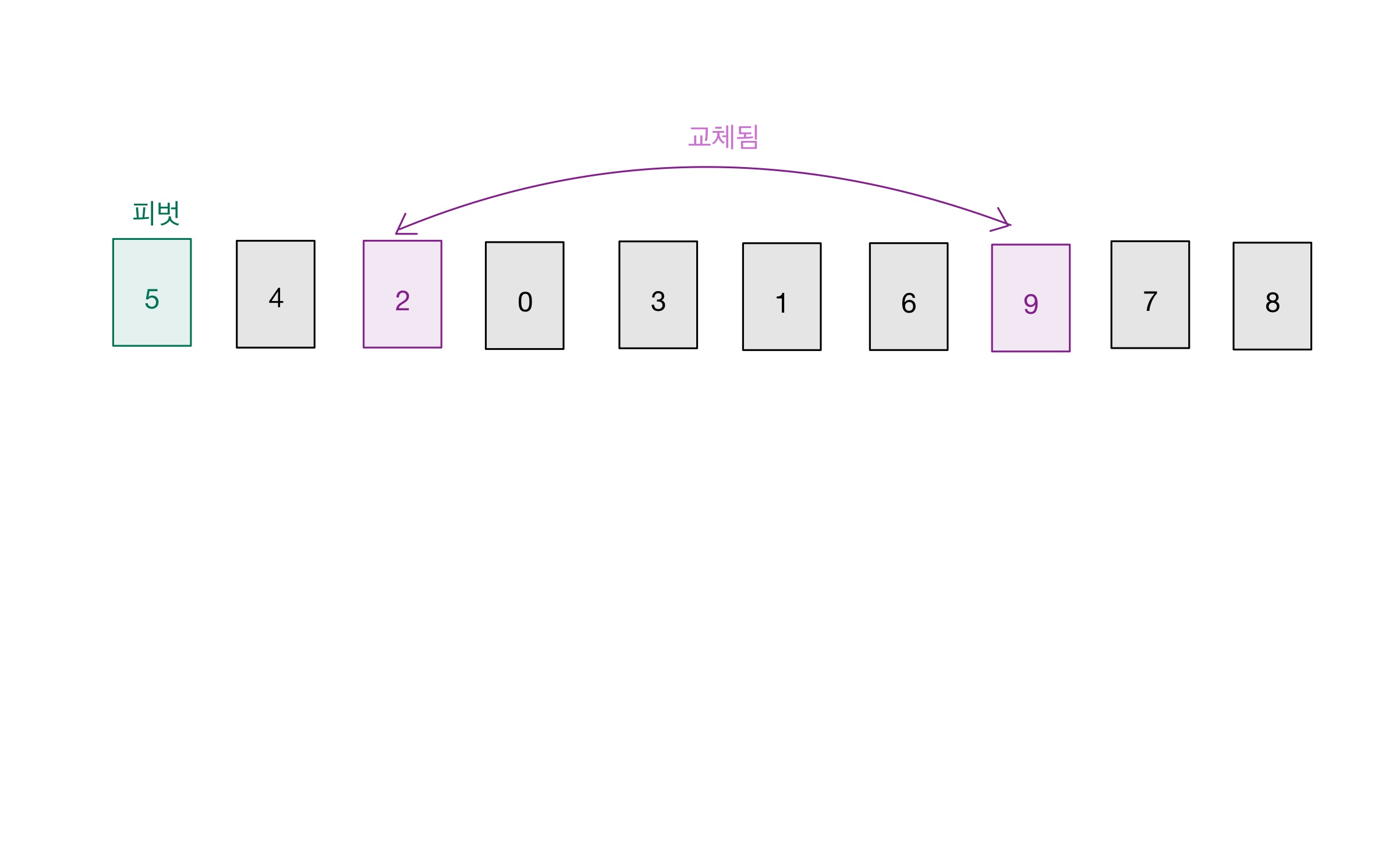
Step 04
Step 05
Step 06
Step 07
Step 08
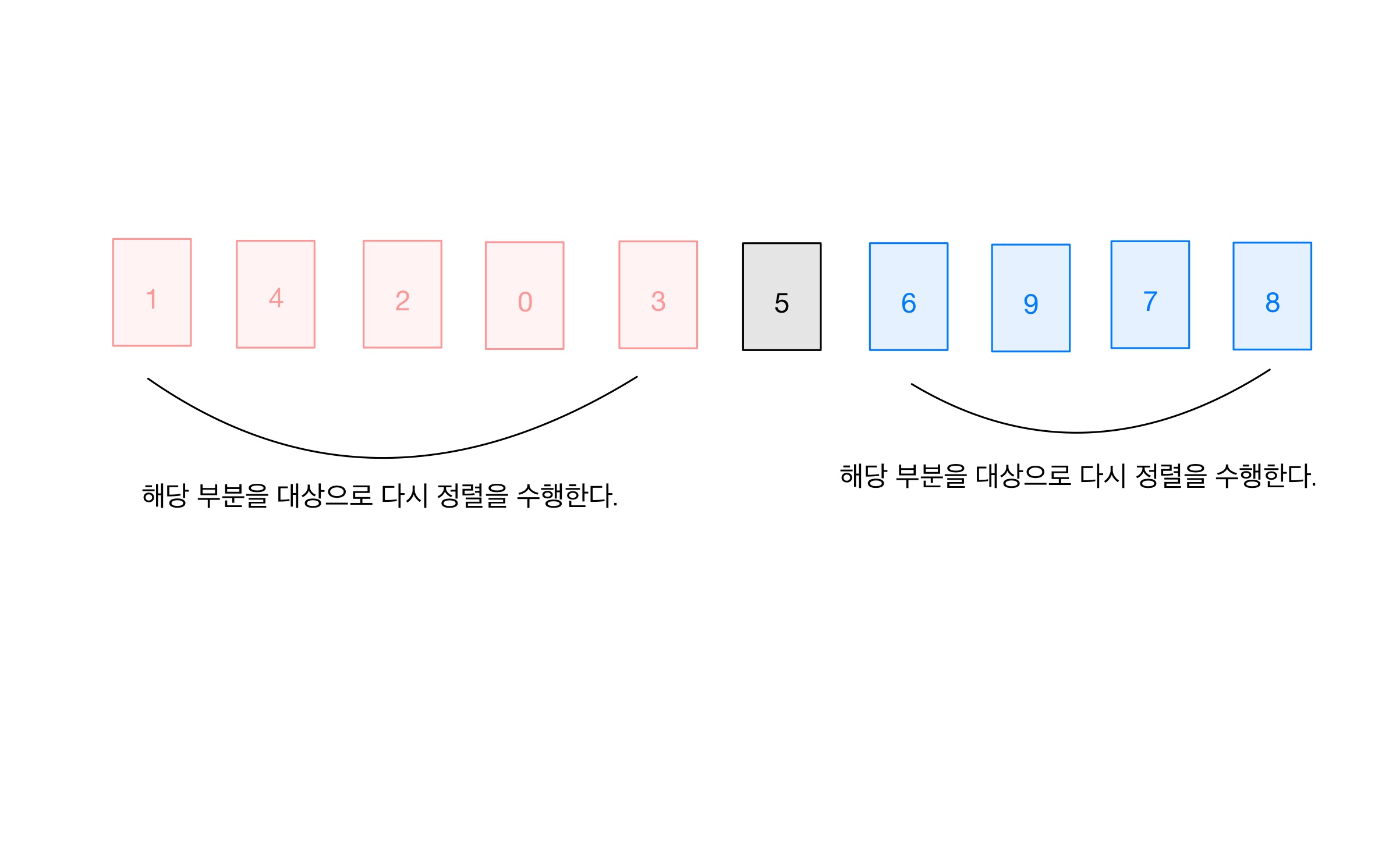
Step 09
각 부분의 수열에 대해 다시 Step1부터 각각 수행한다.
만약 정렬을 수행할 수열의 원소 개수가 1개인 경우, 알고리즘이 종료된다.
결과
- 오름차순으로 정렬되었다.
0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> 9
소스코드
public class 퀵정렬 {
private static void solution(int[] array, int start, int end) {
// start: 배열의 시작점
// end: 배열의 끝점
//만약 배열이 1개 이하라면 재귀 중단
if (start >= end) {
return;
}
int pivot = start; //pivot 설정
int leftPointer = start+1; //pivot 보다 큰 숫자를 찾는 포인터
int rightPointer = end; //pivot 보다 작은 숫자를 찾는 포인터
while (true) {
//pivot보다 큰 수 찾기
while (leftPointer <= end && array[leftPointer] <= array[pivot]) {
leftPointer++;
}
//pivot보다 작은 수 찾기
while (rightPointer > start && array[rightPointer] >= array[pivot]) { //시작점은 피봇이므로 start 미포함
rightPointer--;
}
if (leftPointer > rightPointer) { //교차됐다면
int tmp = array[pivot];
array[pivot] = array[rightPointer];
array[rightPointer] = tmp;
break; //교차시 탈출
} else { //교차 안됐다면
int tmp = array[rightPointer];
array[rightPointer] = array[leftPointer];
array[leftPointer] = tmp;
}
}
solution(array, start, rightPointer-1);
solution(array, rightPointer+1, end);
}
public static void execute() {
Scanner scn = new Scanner(System.in);
int sizeOfN = scn.nextInt();
int[] n = new int[sizeOfN];
scn.nextLine();
for (int i = 0; i < sizeOfN; i++) {
n[i] = scn.nextInt();
}
TimeCheck.start();
solution(n, 0, sizeOfN-1);
for (int i : n) {
System.out.print(i + " ");
}
TimeCheck.end();
}
}
시간복잡도
- 퀵정렬의 평균 시간복잡도는 평균
O(nlogn)으로 알려져있다. - 최선의 경우: 피벗의 위치가 변경되어 분할이 일어날 때마다, 정확히 절반으로 나눠질 경우 ‘분할 횟수가 기하급수적으로 감소’한다.
- 최악의 경우: ‘가장 큰 수’나 ‘가장 작은 수’가 피벗으로 선정되면, 분할 시 수열의 크기를 효과적으로 줄일 수 없기 때문에 연산량이 급격히 늘어난다.
- 이 경우, 시간복잡도는
O(n^2)이 된다.
- 이 경우, 시간복잡도는
- 본 글에서 사용한
호어분할의 경우, 이미 데이터가 정렬되어 있을 때 성능이 매우 안좋다.
- 나동빈, 『이것이 코딩 테스트다』
