컴퓨터 산술
산술논리연산장치 (ALU)
중앙처리장치(CPU)의 구성
- 산술논리연산장치
- ALU
- 산술 및 논리 연산을 수행한다.
- 레지스터
- 제어장치
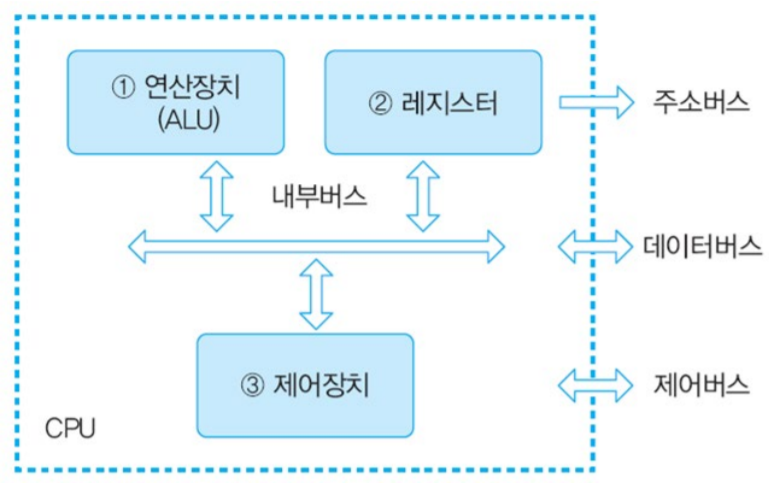
ALU 내부 구성 요소
- 산술 연산장치
- +, -, *, / 등을 수행한다.
- 논리 연산장치
- AND, OR, XOR, NOT 등을 수행한다.
- 시프트 레지스터
- 비트들을 좌우측으로 이동
- 보수기(complementer)
- 2진 데이터를 2의 보수로 변환한다.
- 음수를 만드는 역할을 한다.
- 상태 레지스터(status register)
- 연산 결과의 상태를 나타내는 플래그(flag)들을 저장한다.
ALU의 연산 동작 예시
- ADD AC, B 연산
- AC ← AC + B 라는 의미이다.
- AC: 누산기(레지스터의 일종)
-
연산과정
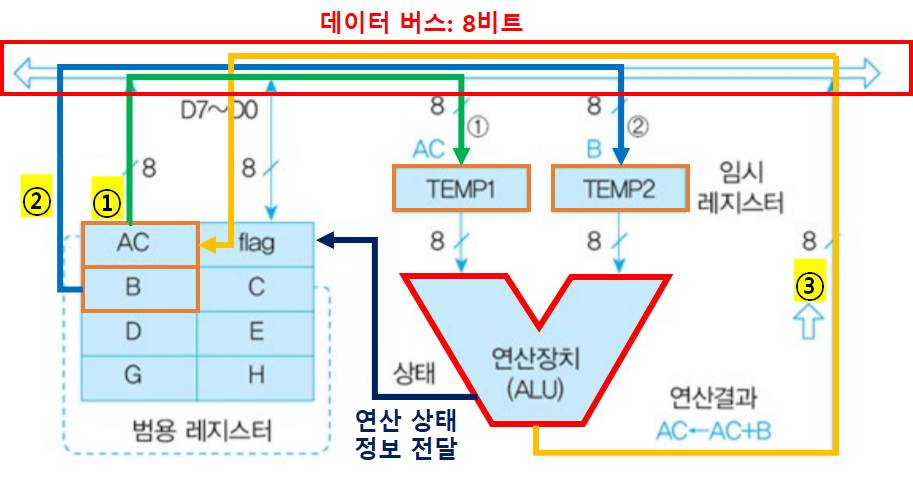
- TEMP1 ← AC
- TEMP2 ← B
- AC ← TEMP1 + TEMP2
정수 표현
10진수의 개념
- {10}=710^2+210^1+4*10^0)
2진수의 개념
- 10진수의 관계는 2의 승수 (
)로 표현한다.
16진수의 개념
- 2진수를 4비트씩 나누어 16진수로 표현한다.
- 0000 ⇒ 0
- 1111 ⇒ F
진법 변환
- 10진수를 2진수로 변환하기
- 연속적으로 2로 나눗셈을 수행하면서 얻어지는 나머지에 의해서 만들어진다.
-
예시
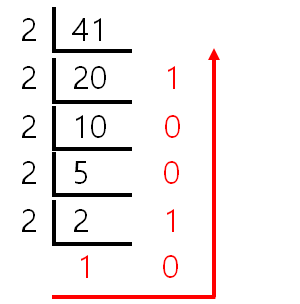
- 결과: 101001
- 2진수를 10진수로 변환
음수의 표현
- 최상위 비트를 부호 비트로 사용한다.
- 0: 양수
- 1: 음수
- 음수 표현 방법
- 부호 크기 표현
- 보수 표현
부호 크기 표현
- 비트 구성요소
- 최상위 비트 = 최상위 비트
- 나머지 비트 = 수의 크기
- 예시) +9 = 0 0001001
- 문제점
- 0의 표현이 2개 존재하므로, 표현할 수 있는 수의 개수가 줄어든다.
- 0 0000000 = +0
- 1 0000000 = -0
- 따라서, n개의 비트로 표현할 수 있는 수가
이 아니라,
이다.
- 0의 표현이 2개 존재하므로, 표현할 수 있는 수의 개수가 줄어든다.
보수 표현
-
음수 = 양수를 표현하는 비트에 2의 보수를 취한 것
- 보수 종류
- 1의 보수: 모든 비트들을 반전시킨다.
- 2의 보수: 1의 보수 + 1
- 예시)
- 1의 보수:
- 2의 보수:
- ‘2의 보수로 표현된 2진수(음수)’를 10진수로 변환하는 방법
- 양수로 변환하여 10진수를 구한 뒤, 그 결과값에 ‘-‘ 부호를 붙인다.
- 예시)
- -9의 2의 보수 =
- 여기에 ‘-‘를 붙인다. ⇒
수의 표현 범위
- 2의 보수로 표현된 n비트 데이터의 표현할 수 있는 수의 범위는 아래와 같다.
- 0이 존재하므로
에 1을 빼야한다.
- 비트에 따른 수의 범위와 최대값과 최소값의 표현
- 8비트 2의 보수
- 16비트 2의 보수
- 8비트 2의 보수
비트 확장
-
비트 확장이란, 부호가 있는 데이터의 비트 수를 늘리는 연산이다.
- 부호화-크기 표현에 비트 확장 연산하기
- +18 = 00010010 (8비트)
- +18 = 00000000 00010010 (16비트)
- -18 = 10010010 (8비트)
- -18 = 10000000 00010010 (16비트)
- 2의 보수 표현에 비트 확장 연산하기
- +18 = 00010010 (8비트)
- +18 = 00000000 00010010 (16비트)
- -18 = 11101110 (8비트)
- -18 = 11111111 11101110 (16비트)
정수의 산술 연산
음수화
- 양수를 음수로 표현하고자 할땐, 2의 보수를 취하여 표현하면 된다.
- 예시)
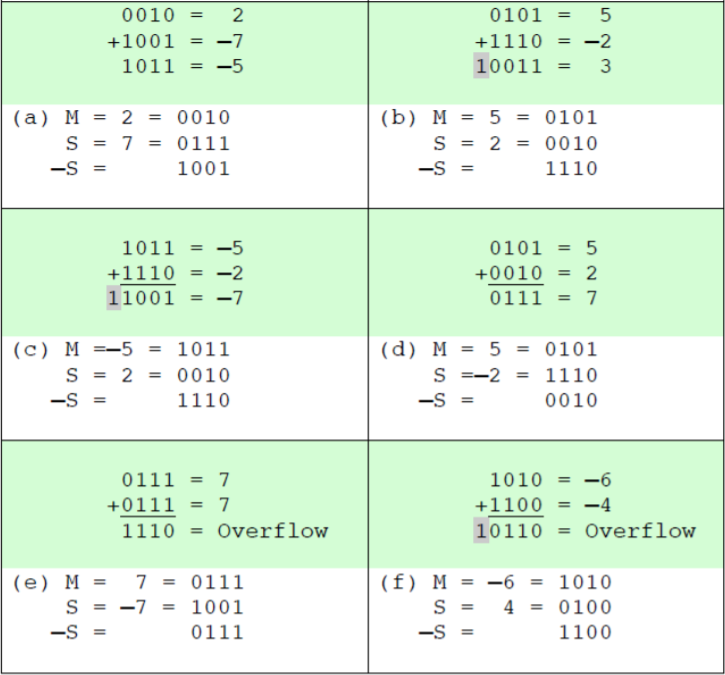
2의 보수로 표현된 수들의 덧셈
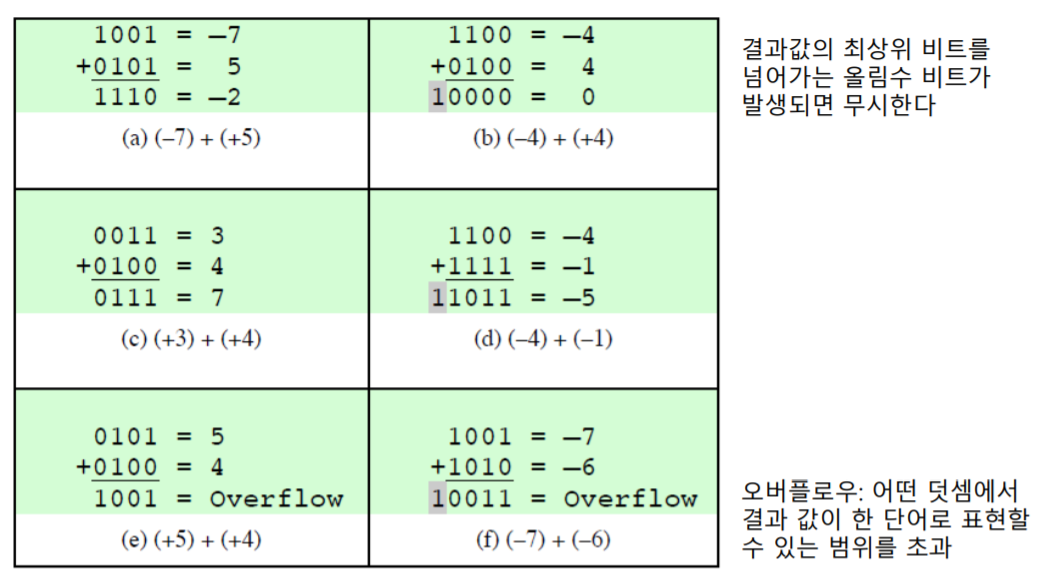
- 오버플로우
- 위의 그림은 총 4비트를 갖는 수에 대한 연산을 나타낸 것이다.
- 4비트로 표현할 수 있는 수의 범위 = -8 ~ +7
의 경우, 연산 결과로 9가 나온다.
- 9는 4개의 비트로 표현할 수 없는 수이다. 따라서, Overflow가 발생한다.
2의 보수로 표현된 수들의 뺄셈
- 감수와 피감수
- A - B
- A: 피감수
- B: 감수
- 뺄셈을 하기 위해선, 감수의 보수를 취한 뒤 그것을 피감수와 더한다.
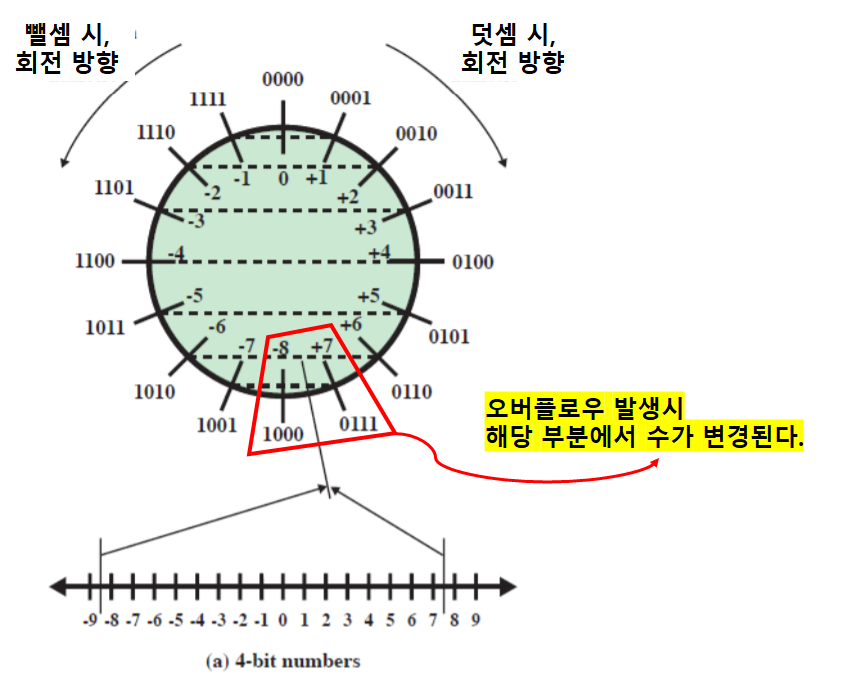
2의 보수 정수들의 기하학적 표현
- 오버플로우 예시
- 총 4비트를 갖는 수에 대해 연산을 했을 때, 오버플로우가 발생하는 상황에 대해 알아보자.
의 경우, 연산 결과로 9가 나온다.
- 9는 4개의 비트로 표현할 수 없는 수이다. 따라서, Overflow가 발생한다.
- 이 경우,
의 결과로 -7이 도출된다.
- 왜냐하면 위 그림에서 덧셈 회전방향으로 회전시, +7 이후는 -8이기 때문이다.
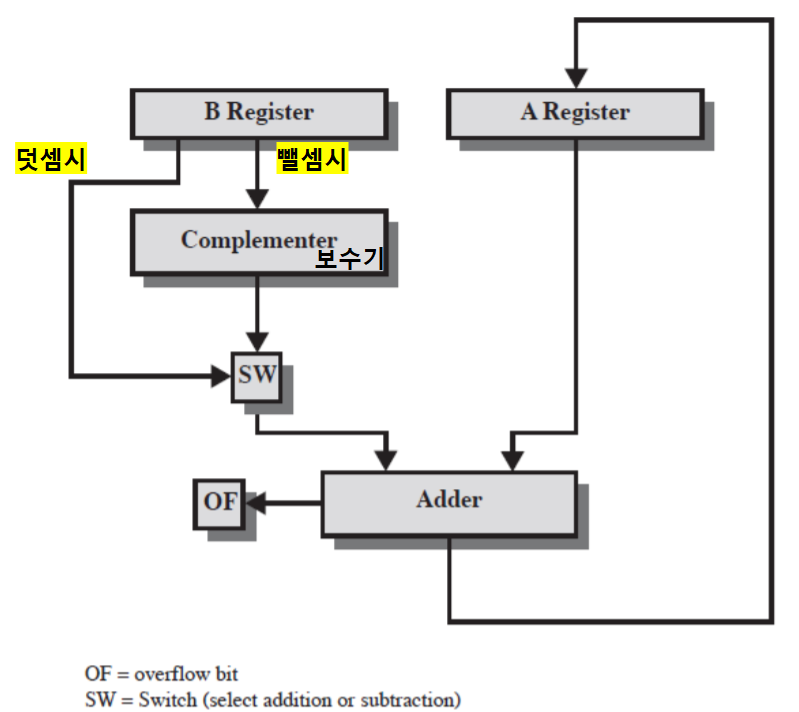
덧셈/뺄셈 하드웨어 흐름
곱셈
- 피승수
- 곱해지는 수
- M
- 승수
- 곱하는 수
- Q
- 예시
- 5 * 10
- 피승수: 5
- 승수: 10
-
부호가 없는 경우의 곱셈의 예
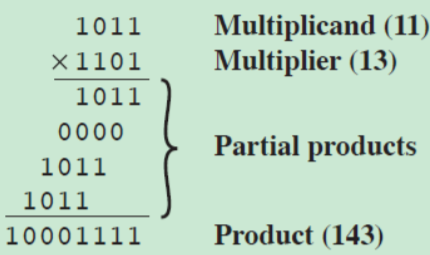
-
4비트의 두 수가 서로 곱셈을 수행하면, 2배인 8비트의 길이의 결과를 출력한다.
-
컴퓨터에서의 계산 예시
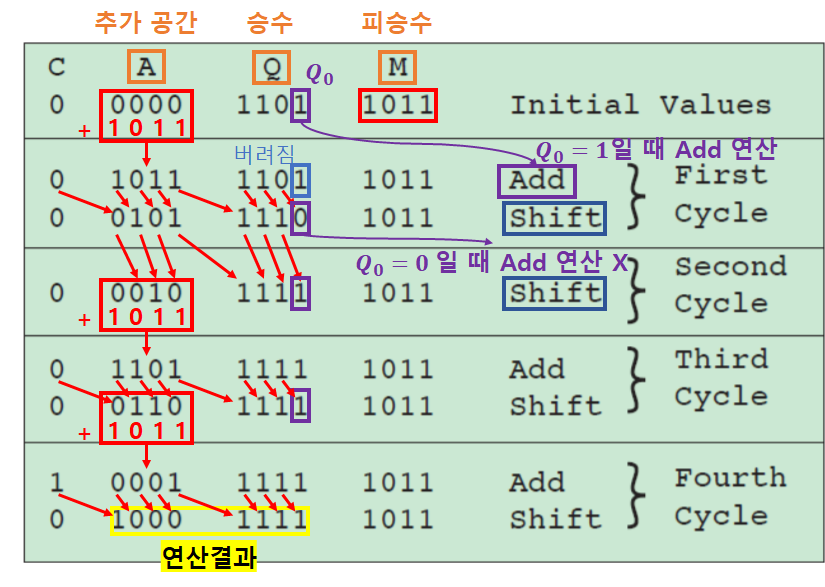
-
부호없는 2진 곱셈 흐름도
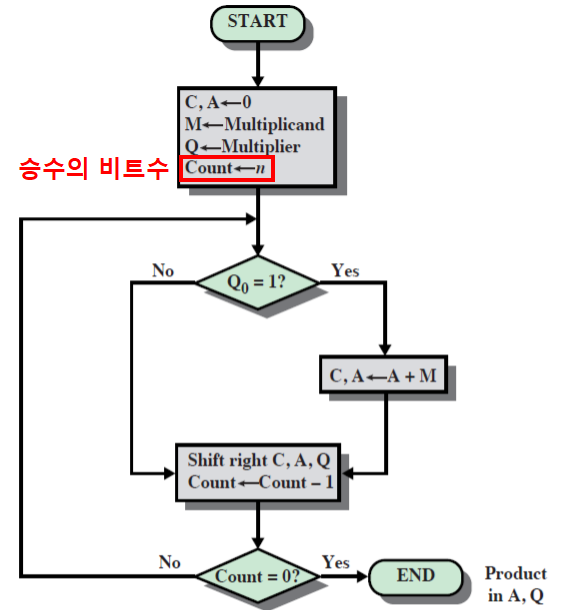
-
- 부호있는 두 수의 곱셈: Booth 알고리즘
- 연산 순서
- 승수와 피승수를 Q와 M 레지스터에 저장
의 오른쪽에
라는 한 비트 레지스터 추가
: Q 레지스터의 LSB (가장 오른쪽 비트)
와
가 같은 경우
,
,
레지스터의 모든 비트를 우측으로 반 비트씩 산술시프트한다.
와
가 0 , 1 인 경우
- 피승수를
에 더한다.
- 그리고 우측 산술시프트 한다.
- 피승수를
와
가 1 , 0 인 경우
로부터 피승수를 뺀다.
- 그리고 우측 산술시프트 한다.
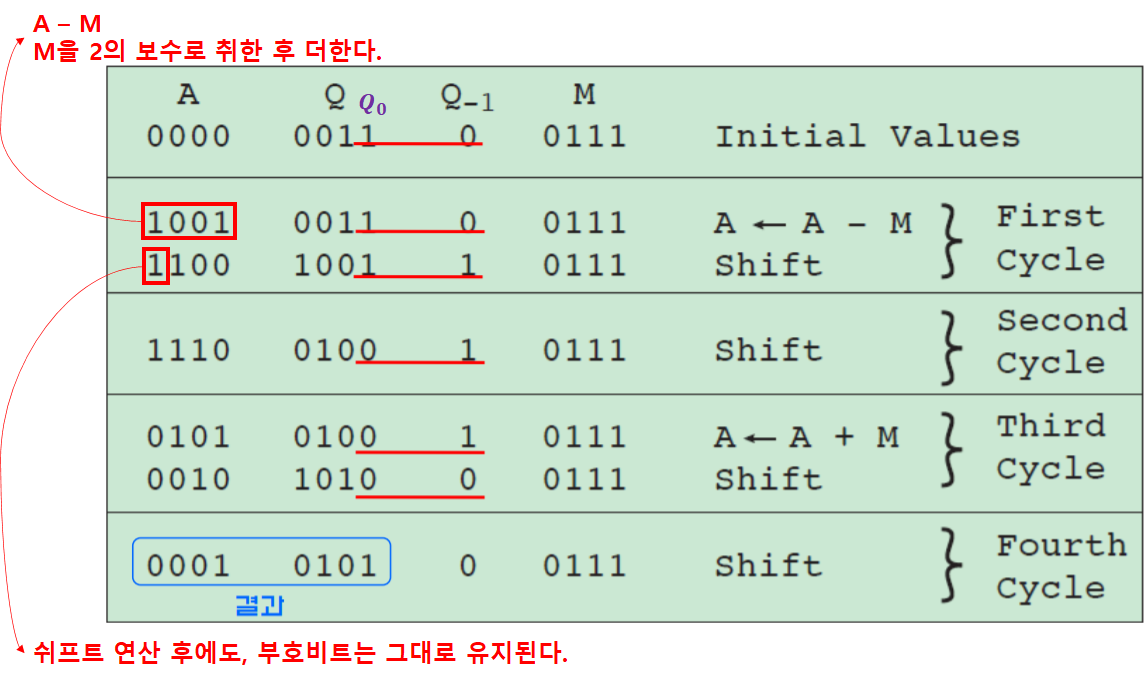
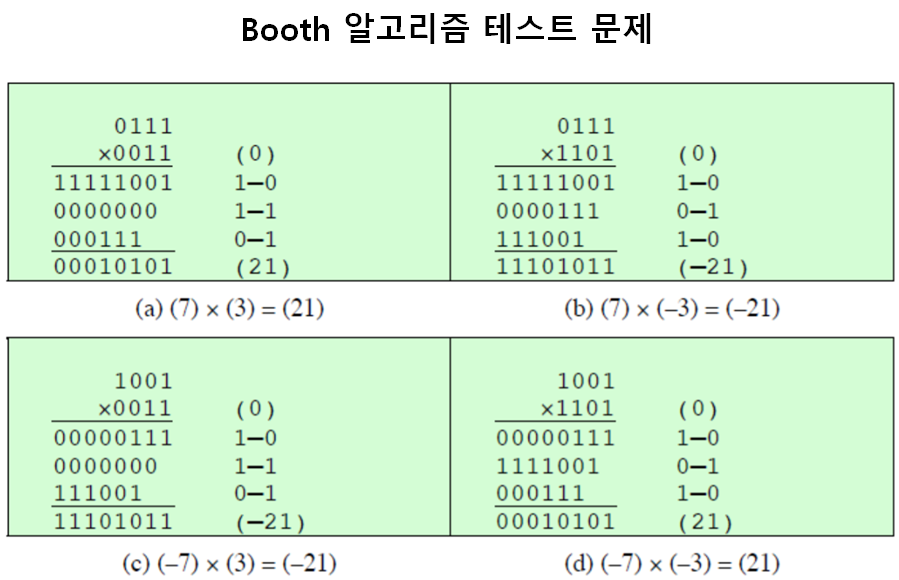
- 연산 순서
나눗셈
- 피제수
- 나눠지는 수
- Q
- 제수
- 나누는 수
- M
- 음수에서의 나눗셈
- 피제수 = 제수 * 몫 + 나머지
- 7 / -3
- 7 = -3 * -2 + 1
- -7 / -3
- -7 = -3 * 2 - 1
-
부호없는 2진 나눗셈 흐름도
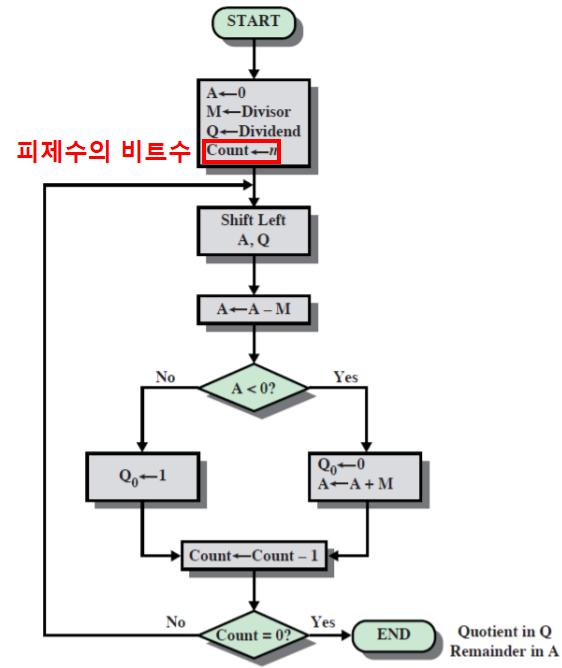
-
나눗셈 예시: 7/3
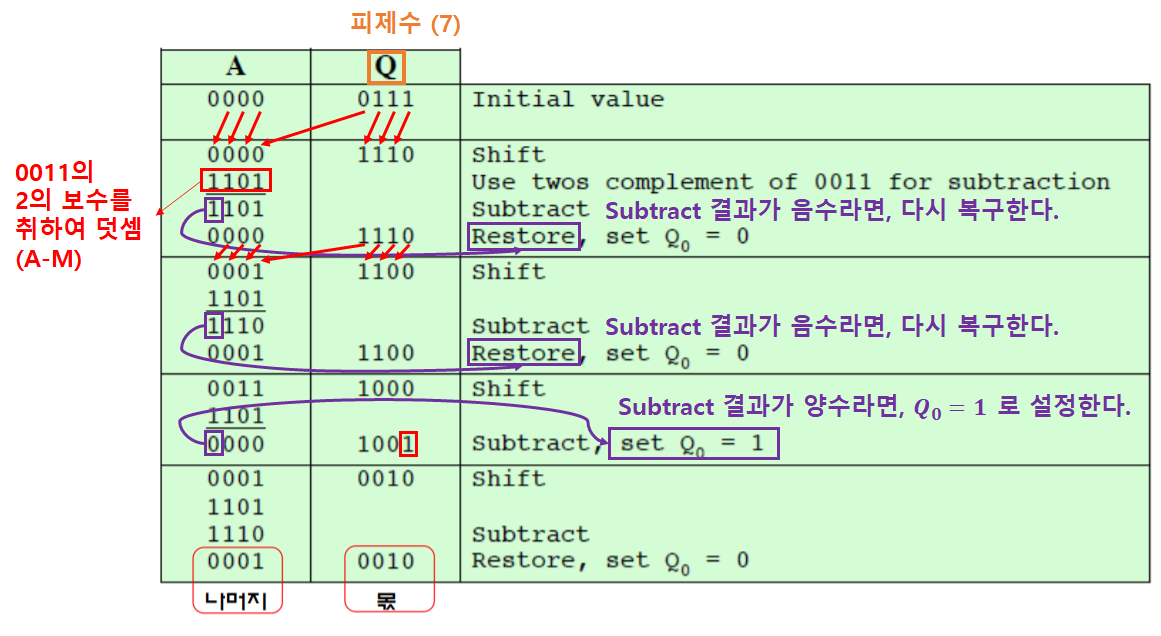
부동소수점 표현
소수점 표현의 종류
- 고정소수점 표현 방식
- 매우 큰 수 및 매우 작은 수의 표현이 불가능하다.
- 부동소수점 표현 방식
- 과학적 표기의 지수를 사용하여 소수점의 위치를 이동시킬 수 있는 표현 방법이다.
- 표현의 범위가 확대된다.
- 십진수에 대한 부동 소수점 표현 예시
부동소수점 수의 표현법
- S : 가수 (significand)
- B : 기수 (base)
- E : 지수 (exponent)

정규화된 표현
- 지수의 값에 따라, 동일한 수에 대한 부동소수점 표현이 여러가지 존재한다.
- 예시)
- 예시)
- 따라서 부동소수점의 수를 통일되게 표현해야 한다. ⇒ 정규화된 표현
- 무조건 앞은 1이 위치해야 한다.
- 예시
- 정규화 X
- 정규화 O
- 정규화 X
가수
- 정규화된 표현에서 가수의 맨 좌측 비트는 항상 1로 정해져 있으므로 가수 필드에 저장할 필요가 없다.
기수
- 기수는 묵시적이며, 모든 수에 동일하므로 저장할 필요가 없다.
- 즉 2진수로 저장되므로, 기수는 무조건 2이다.
지수 (바이어스된 표현)
- 지수는 부호를 가지므로 이에 대한 표현이 필요하다.
- 따라서, 바이어스된 표현을 사용하여 필드에 저장한다.
- 바이어스된 표현
- 필드에 저장시
- (본래 지수값) + 127
- 필드에서 추출시
- (저장된 바이어스된 지수값) - 127
- 필드에 저장시
보통 바이어스화 할 때, 127를 더한다.
- 예시
- 지수값:
- 바이어스된 지수 표현:
- 즉,
대신
로 필드에 저장한다.
- 즉,
- 지수값:
부동소수점 표기 연습문제 (1)
- 문제
- 10진수 -13.625를 32비트 부동소수점 형식으로 표현하라.
- 풀이
에서 1 추출 ⇒ 소수점 첫번째 자리
에서 0 추출 ⇒ 소수점 두번째 자리
에서 1 추출 ⇒ 소수점 세번째 자리
- 따라서, 소수점 부분은
- 부호비트: 1 (음수)
- 가수부:
(좌측의 1은 제외한다.)
- 지수부:
⇒
(바이어스 더하기)
-
결과

부동소수점 표기 연습문제 (2)
- 문제
- 32비트 부동소수점으로 표현된 아래 수에 대한 10진수는?
- 0 10000011 101 0000 0000 0000 0000 0000
- 풀이
- 부호비트: 0 (양수)
- 가수부:
⇒
- 생략된 1 다시 가져오기
- 지수부:
- 결과
전형적인 32비트 형식으로 표현 가능한 수의 범위
- 정수
~
- 총
가지의 수를 표현할 수 있다.
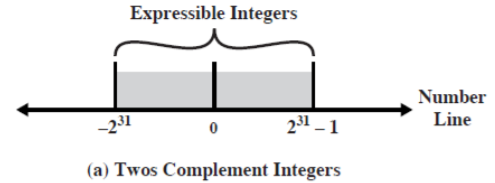
- 부동소수점수
~
~
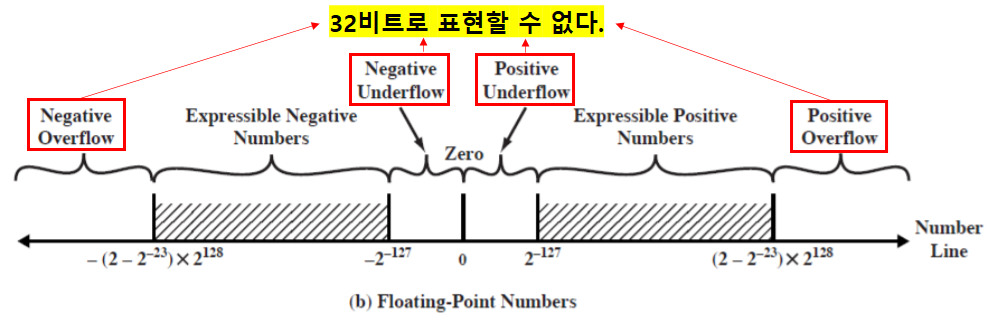
부동소수점의 밀도
- 비트할당 문제
- 표현하는 수의 범위와 정밀도를 결정해야 한다.
- 지수 필드의 비트 수가 늘어날 때
- 소수점을 이동시키는 범위가 커져서 표현 가능한 수의 범위가 확장된다.
- 가수 필드의 비트 수가 늘어날 때
- 이진수로 표현할 수 있는 수가 많아져서 정밀도가 증가한다.
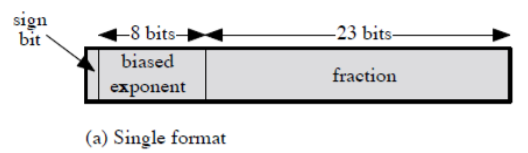
IEEE 754 formats
- IEEE 754 formats 은 부동 소수점 비트 포멧의 표준이다.
-
32비트
-
64비트

부동소수점의 산술연산
개요
- 가수와 지수의 연산을 분리해서 수행한다.
- 덧셈과 뺄셈
- 지수를 같은 값으로 조정한 후, 가수들에 대해 덧셈과 뺄셈을 수행한다.
- 이때 지수는 “피연산자들의 지수 중 큰 것으로 통일”한다.
- 곱셈과 나눗셈
- 가수끼리는 곱셈과 나눗셈을 수행한다.
- 곱셈
- 지수 연산 시 덧셈
- 나눗셈
- 지수 연산 시 뺄셈
부동소수점 수의 덧셈과 뺄셈
- 절차
- 피연산자들이 0인지 검사한다.
- 두 수의 지수들을 같아지도록 가수의 자리수를 조정한다.
- 큰 값으로 조정한다.
- 가수들 간에 덧셈/뺄셈을 수행한다.
- 가수들의 부호를 고려해서 더해진다.
- 결과를 정규화한다.
- 가장 왼쪽 비트가 0이 아닐 때까지, 좌측으로 쉬프트시킨다.
-
이진수의 부동소수점 수의 덧셈 예시
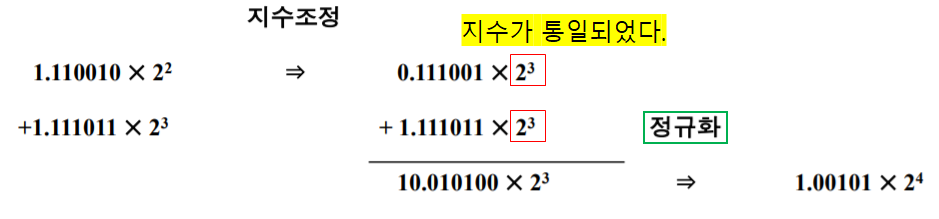
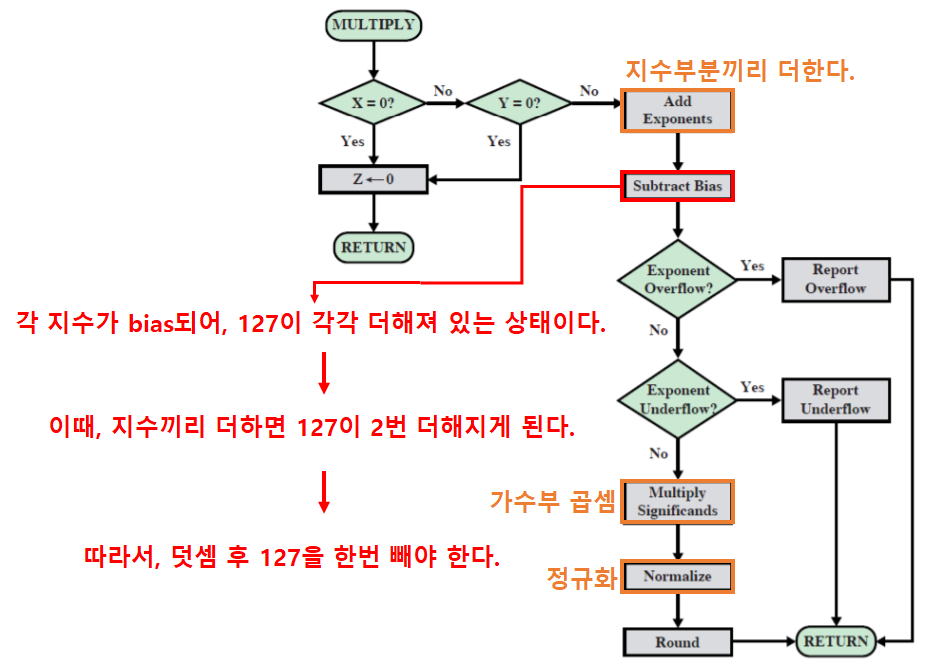
부동소수점 수의 곱셈
- 가수끼리는 곱셈 연산을 수행하고 지수끼리는 덧셈을 수행한다.
-
연산 워크플로우
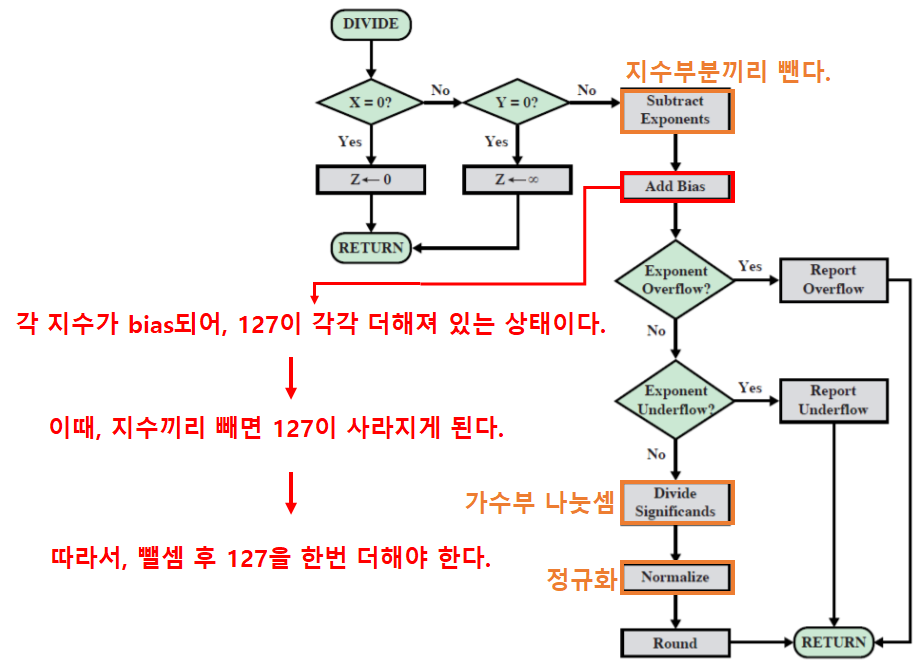
부동소수점 수의 나눗셈
- 가수부분은 나눗셈 연산을 수행하고, 지수부분은 뺄셈 연산을 수행한다.
-
연산 워크플로우
논리 연산
개요
- ALU에서 L에 해당되는 연산이다.
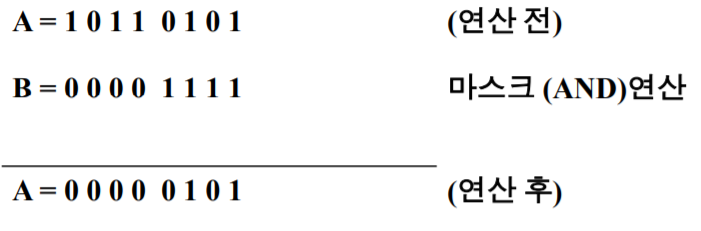
마스크 연산
- 원하는 비트들을 선택적으로 clear(0으로 만들기)하는데 사용하는 연산이다.
-
A 레지스터의 상위 4비트를 0으로 clear하는 경우의 예시
비교 연산
- 두 데이터를 비교하는 연산이다.
- 대응되는 비트들의 값이 같으면, 해당 비트를 0으로 설정한다.
- 대응되는 비트들의 값이 다르면, 해당 비트를 1으로 설정한다.
- 모든 비트들이 같은 경우, Z 플래그 (zero 플래그)를 1로 설정한다.
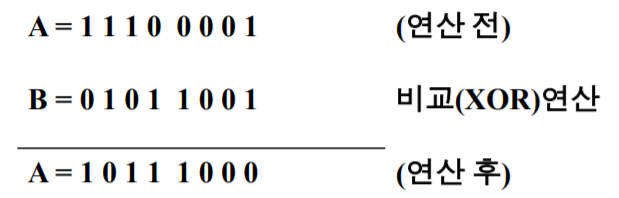
산술적 쉬프트
- 쉬프트 과정에서 부호 비트는 유지하고, 수의 크기를 나타내는 비트들만 쉬프트한다.
- 쉬프트 종류
- 산술적 좌측-쉬프트
- D4(불변) , D4←D3 , D3←D2 , D2←D1
- 산술적 우측-쉬프트
- D4(불변) , D4→D3 , D3→D2 , D2→D1
- 산술적 좌측-쉬프트
-
예시

- 성결대학교 컴퓨터 공학과 최정열 교수님 (2021)
- William Stalling, 『컴퓨터시스템구조론(10판)』
