캐시 기억장치
개요
캐시 기억장치란?
- 기억장치 속도가 가장 빠른 기억장치의 속도에 근접하도록 한다.
- 저렴한 반도체 기억장치의 가격으로 큰 기억장치 용량을 가지도록 한다.
- 주기억 장치 내용의 일부분을 복사하여 저장한다.
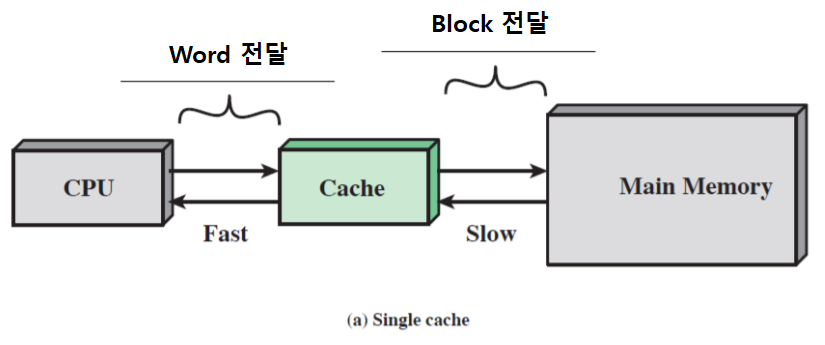
캐시 기억장치의 기본 동작
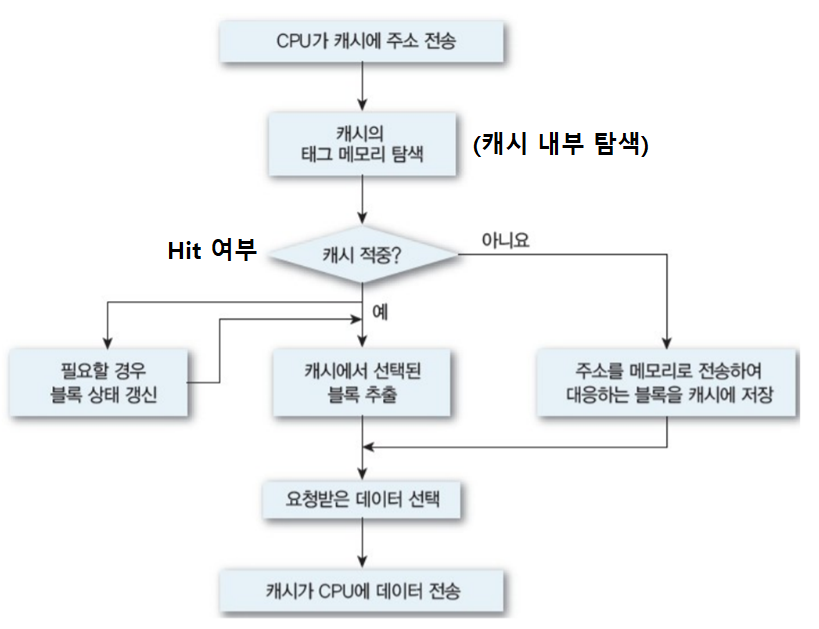
캐시와 주기억장치 조직
-
Main Memory
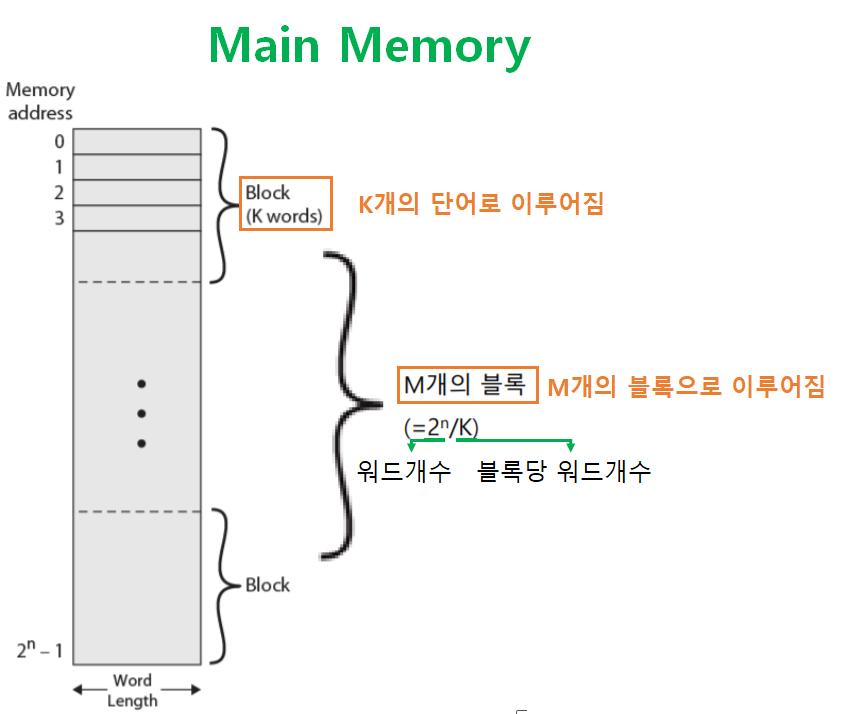
-
캐시
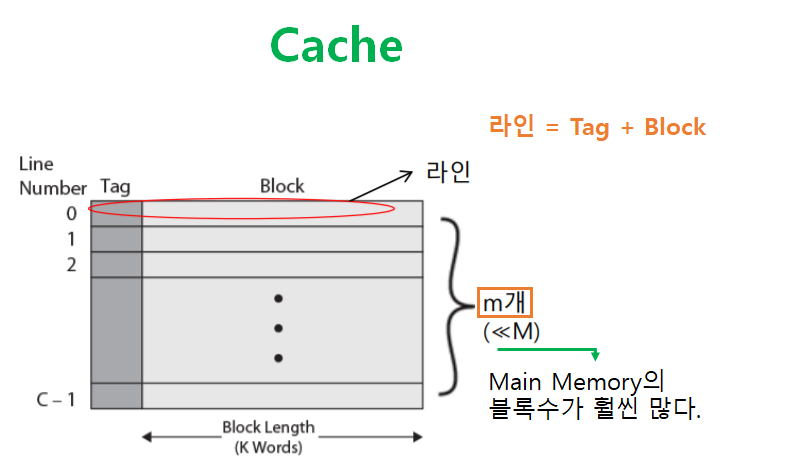
-
Main Memory vs Cache
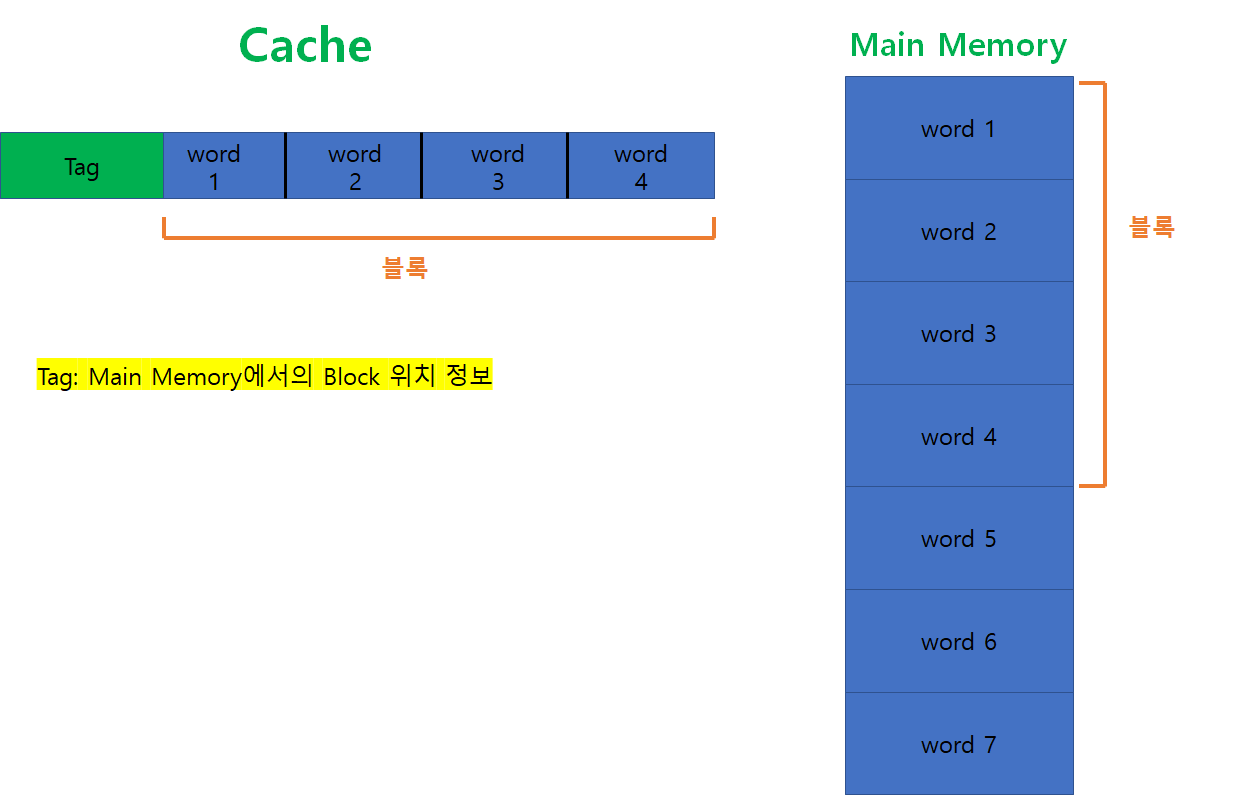
전형적인 캐시 조직
캐시 설계 요소들
설계 요소 종류
캐시를 설계하는데 고려해야하는 요소들은 아래와 같다.
- 캐시 주소
- 캐시 크기
- 매핑 함수
- 교체 알고리즘
- 쓰기 정책
- 라인 크기
- 캐시 개수
지금부터 하나씩 알아보자.
캐시 주소
논리적 캐시 (가상 캐시)
- 가상 기억장치
- 주기억장치의 크기와 상관없이 논리적인 관점으로 기억장치의 위치를 지정해준다.
- 논리적 캐시
- 논리적 캐시는 가상 주소를 이용하여 데이터를 저장한다.
- 만약 논리적 캐시에서 hit 한다면, MMU를 통하지 않고 캐시를 직접 액세스한다.
- MMU
- Memory Management Unit
- 기억장치 관리 유닛
- 프로세서가 가상주소를 참조하면 MMU가 물리주소로 변환해준다.
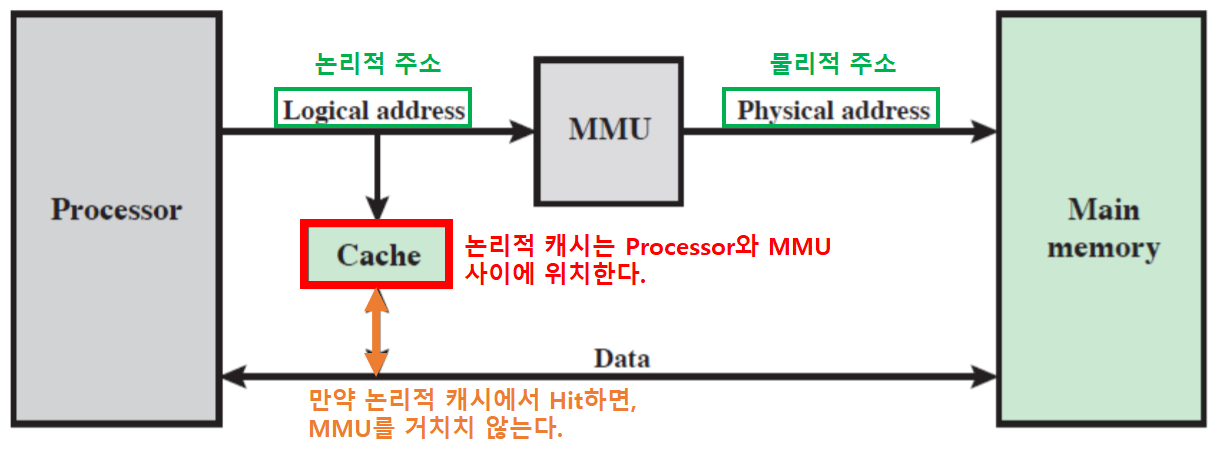
- Processor와 MMU 사이에 캐시가 존재한다면, 그것은 논리적 캐시이다.
- 그렇기 때문에 가상 주소를 갖는 데이터가 논리적 캐시에 존재하면, MMU를 거치지 않아도 된다.
- 장점
- 물리적 캐시보다 빠르다.
- 단점
- 논리적으로 동일한 주소를 갖더라도, 실제 물리적 주소는 다를 수 있다.
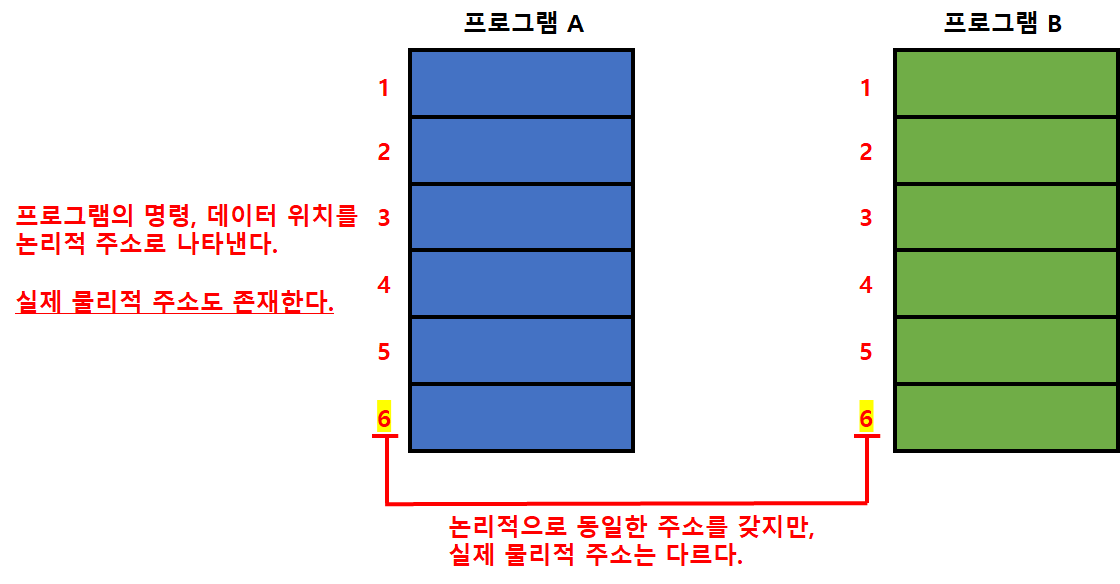
물리적 캐시
- MMU와 Main Memory 사이에 캐시가 존재한다면, 그것은 물리적 캐시이다.
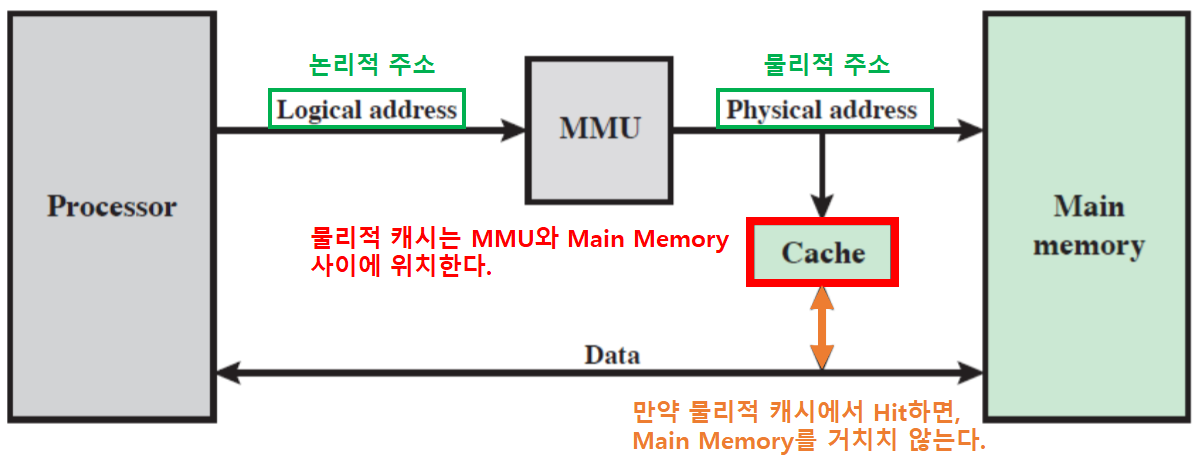
- 물리적 주소는 실제 Main Memory의 주소를 의미한다.
캐시 크기
캐시 크기 목표
- 전체적으로 비트당 평균 비용이 “주기억 장치만의 평균비용”과 비슷해질만큼 충분히 작아야한다.
- 전체 평균 액세스 시간이 “캐시의 액세스 시간”에 접근할 만큼 충분히 커야한다.
- 즉, 캐시 크기를 최소화 해야 한다.
캐시 크기의 최소화 이유
- 캐시의 용량이 커질수록 속도가 느려진다.
- 칩과 보드상의 공간에 제약을 받는다.
캐시와 주기억장치 간의 주소 매핑
사상 함수
- 사상 함수란?
- ‘주기억장치의 Block’을 ‘캐시의 Line’으로 사상(매핑)해주는 알고리즘이다.
- 사상 함수 필요성
- 캐시의 Line 수는 주기억장치의 Block 수보다 적으므로, 이들을 어떻게 매핑할 것인가가 중요하다.
- 사상 함수의 종류
- 직접 사상
- 연관 사상
- 세트 연관 사상
-
매핑 구조
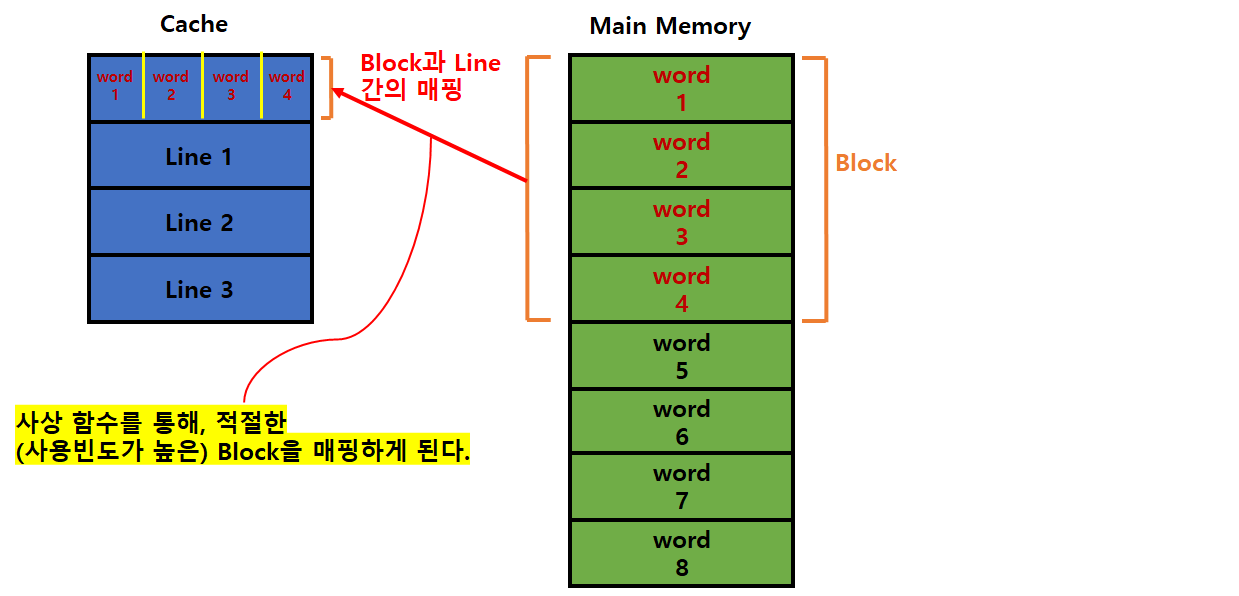
그림에선 캐시의 Line 중 Tag 부분이 빠졌지만, 실제로는 존재한다.
이해를 위한 그림임을 참고하자.
지금부터 여러 사상 함수의 종류에 대해 알아보자.
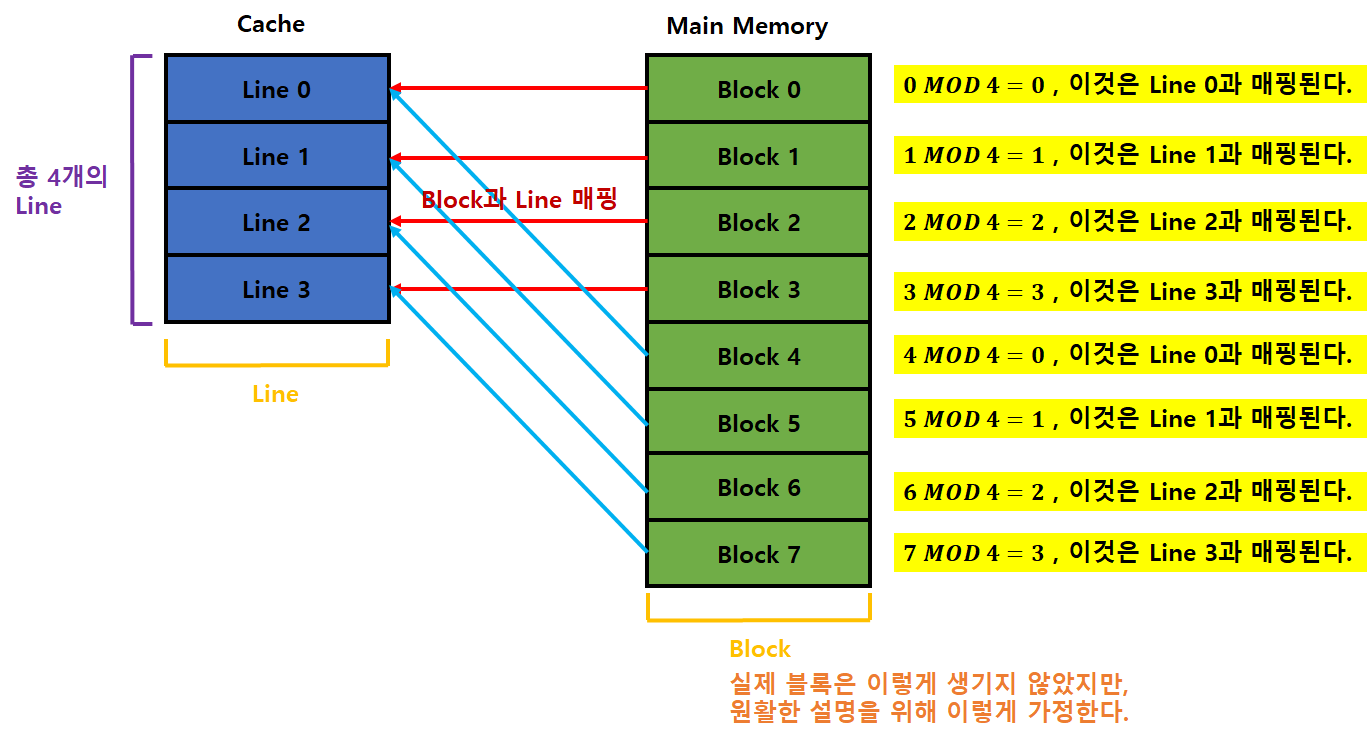
직접 사상
- 주기억 장치의 각 Block을 한 개의 캐시 Line으로만 사상(매핑)한다.
- 즉, Block들은 각자 지정된 Line으로 매핑된다.
- 매핑시 사용되는 함수
: 매핑할 캐시 Line 번호
: 매핑될 주기억장치 Block 번호
: 캐시 내의 총 Line 개수
: 나머지 연산자
-
원리
-
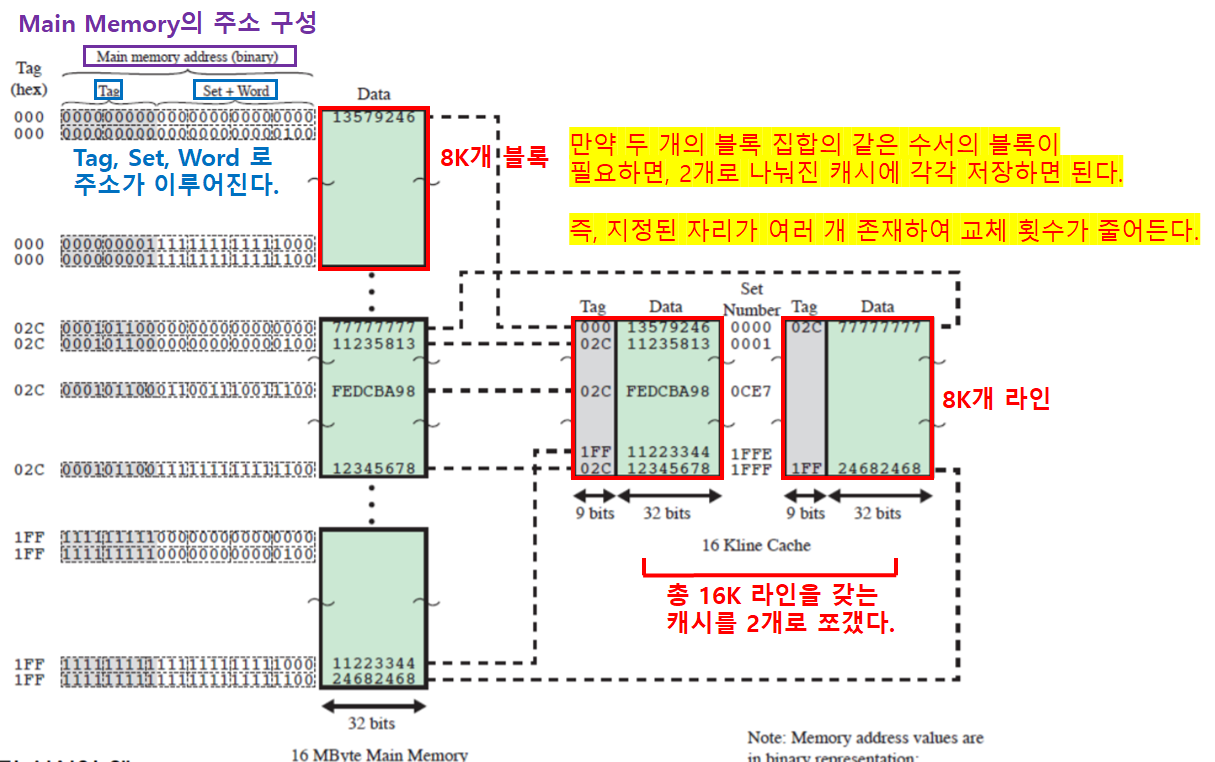
Cache와 Main Memory 관계
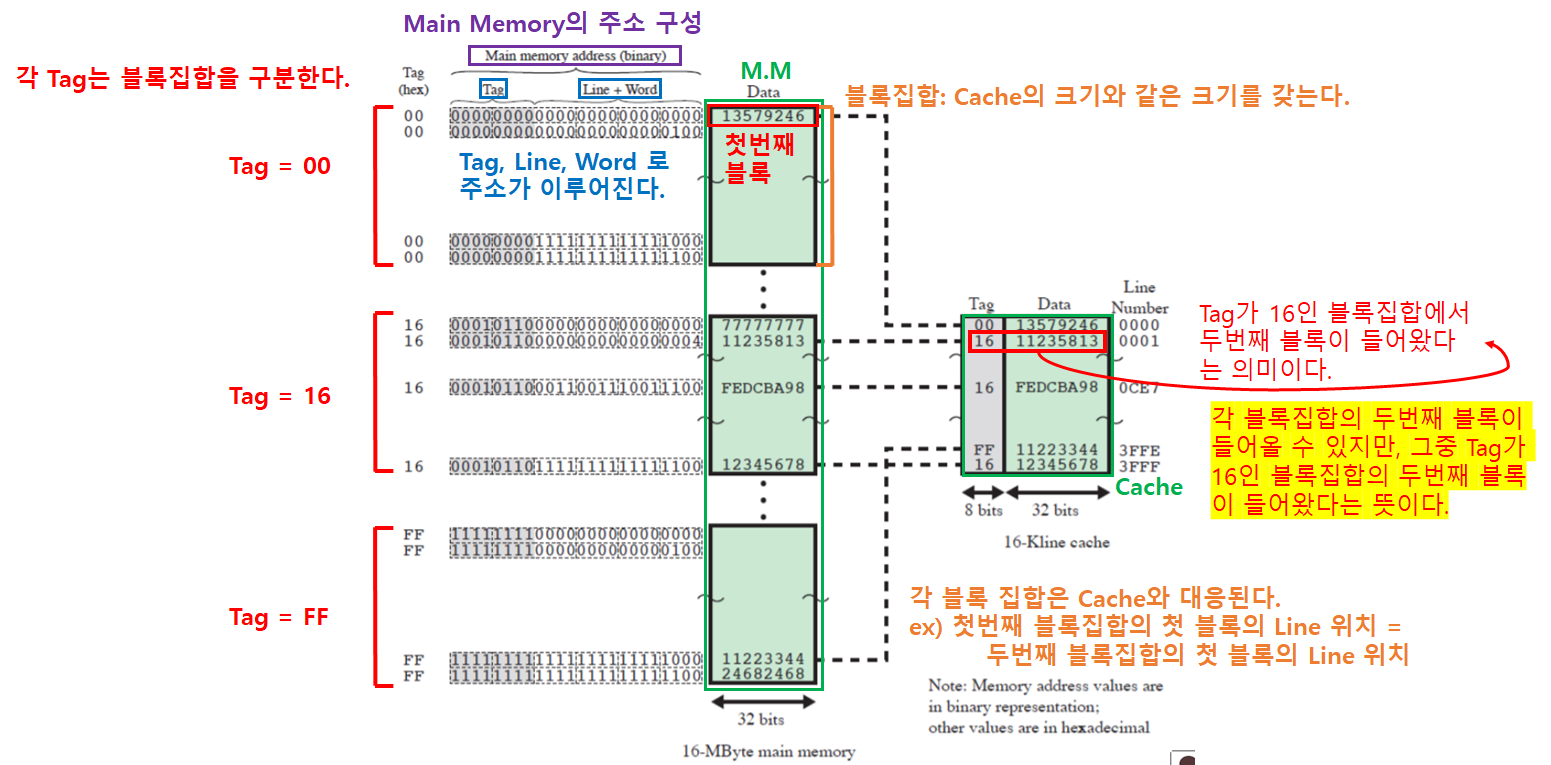
- 각 블록집합은 서로 같은 위치에 존재하는 블록끼리 캐시 Line을 경합하게 된다.
- 만약, 위 그림에서 ‘13579246’ 블록과 ‘77777777’ 블록을 프로세서가 필요해하면, 캐시에서 교체가 이루어진다.
- 왜냐하면, ‘13579246’ 블록과 ‘77777777’ 블록이 서로 같은 Line 위치를 사용하기 때문에 공존할 수 없다.
- Main Memory의 주소는 ‘Tag’, ‘Line주소’, ‘Word주소’로 이루어진다.
- Tag: 각 블록 집합을 구분한다.
- Line 주소: Tag로 블록 집합 내에서 어떤 블록인지 구분한다.
- Word 주소: Line 주소로 특정된 블록 내에서 어떤 워드인지 구분한다.
- 직접 사상 방식의 장단점
- 장점
- 간단하고 구현 비용이 적게든다.
- 단점
- 어떤 블록이 들어갈 수 있는 캐시 위치가 고정되어, 적중률이 낮다.
- 캐시에 빈공간이 있어도, 지정된 위치가 있기 때문에 miss가 발생할 가능성이 높다.
- 장점
직접 사상: 예시 문제
- 데이터 크기와 이진수
- KBits =
- MBits =
- KBits =
- 가정
- Cache 크기 = 64KBits
- Main Memory 크기 = 16MBits
- Word 크기 = 1Bits
- Block 크기 = 4Bits
- 문제
- 이때, M.M (Main Memory)의 주소의 비트수는?
- M.M의 주소 비트수 =
(M.M의 크기/Word의 크기) =
비트
n개의 비트로 표현할 수 있는 2진수 개수 =
- M.M의 주소 비트수 =
- 블록 집합의 개수는?
- 블록집합 개수 = M.M크기/Cache크기 = 16MBits/64KBits =
개
- 블록집합 개수 = M.M크기/Cache크기 = 16MBits/64KBits =
- Main Memory의 주소에서 Tag의 비트수는?
- Tag는 각 블록 집합을 구분하는 구분자이다. 따라서, 블록집합의 개수만큼 표현할 수 있는 비트 개수가 필요하다.
- Tag 비트수 =
(블록집합 개수) =
비트
- Main Memory의 주소에서 Line 주소의 비트수는?
- Line 주소는 이미 특정된 블록 집합 내의 Line들을 구분하는 역할을 한다. 따라서, 블록 집합 내의 Line의 개수만큼 표현할 수 있는 비트 개수가 필요하다.
- Line 주소의 비트수 =
(한 블록집합에서의 Line의 개수) =
(캐시크기/블록(Line)크기) =
(64KBits/4Bits) =
비트
- Main Memory의 주소에서 Word 주소의 비트수는?
- Word 주소는 이미 특정된 블록 내의 Word들을 구분한다. 따라서, 블록 내의 Word 개수만큼 표현할 수 있는 비트 개수가 필요하다.
- Word 주소 비트수 =
(블록당 Word 개수) =
(블록크기/Word크기) =
(4B/1B) =
비트
- M.M (Main Memory)의 주소의 구성
- Tag길이 + Line주소길이 + Word주소길이 = M.M의 주소 길이
- 8 + 14 + 2 = 24 비트
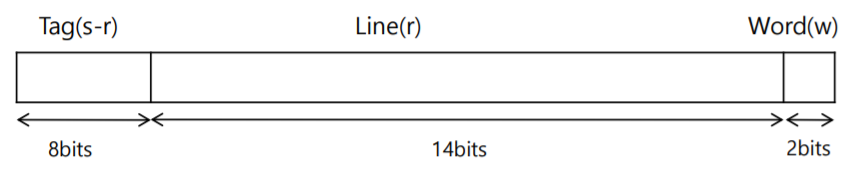
- 이때, M.M (Main Memory)의 주소의 비트수는?
연관 사상
- 주기억장치의 블록이 캐시의 어떤 라인으로도 적재될 수 있도록 허용한다.
- 태그 필드만으로 주기억장치의 블록을 구분할 수 있다.
- 그 블록이 캐시에 있는지 확인하기 위해, 태그가 일치하는 모든 라인과 비교해야 한다.
- 즉 Hit하는지 확인하려면, 모든 라인을 찾아봐야 한다. ⇒ 성능저하
-
원리
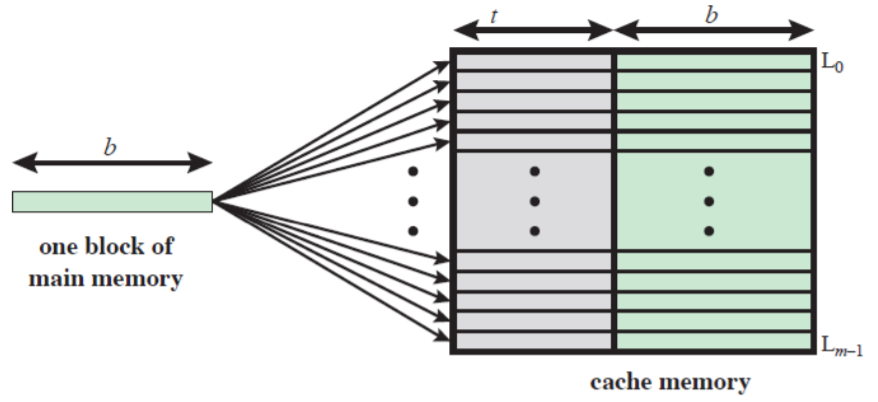
-
Cache와 Main Memory 관계
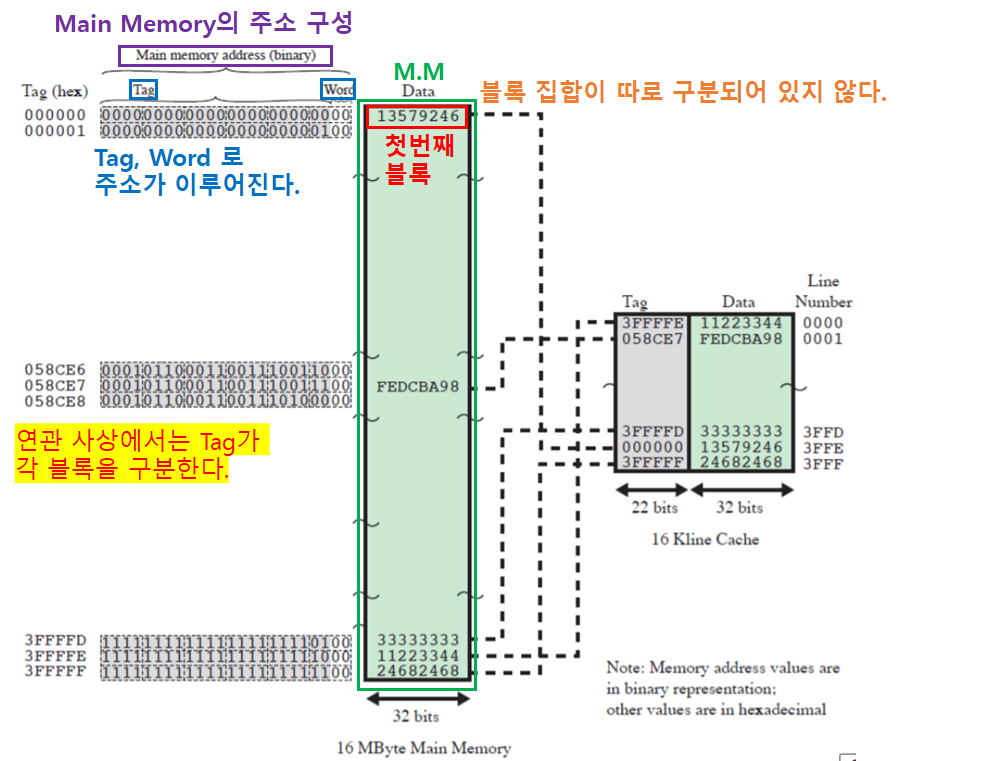
- 연관 사상 방식의 장단점
- 장점
- 새로운 블록이 캐시로 읽혀질 때, 블록을 교체하는데에 있어서 융통성이 있다.
- 단점
- 캐시 라인들의 태그들을 병렬로 검사하기 위한 복잡한 회로가 필요하다.
- Hit하는지 확인하려면, 모든 라인을 찾아봐야 한다. ⇒ 성능저하
- 장점
연관 사상: 예시 문제
- 가정
- Cache 크기 = 64KBits
- Main Memory 크기 = 16MBits
- Word 크기 = 1Bits
- Block 크기 = 4Bits
- 문제
- Main Memory의 주소에서 Tag의 비트수는?
- 연관 사상에서 Tag는 각 블록을 구분하는 구분자이다.(블록 집합 X) 따라서, 블록의 개수만큼 표현할 수 있는 비트 개수가 필요하다.
- Tag 비트수 =
(블록 개수) =
(M.M크기/블록크기) =
비트
- Main Memory의 주소에서 Word 주소의 비트수는?
- Word 주소는 이미 특정된 블록 내의 Word들을 구분한다. 따라서, 블록 내의 Word 개수만큼 표현할 수 있는 비트 개수가 필요하다.
- Word 주소 비트수 =
(블록당 Word 개수) =
(블록크기/Word크기) =
(4B/1B) =
비트
- M.M (Main Memory)의 주소의 구성
- Tag길이 + Word주소길이 = M.M의 주소 길이
- 22 + 2 = 24 비트
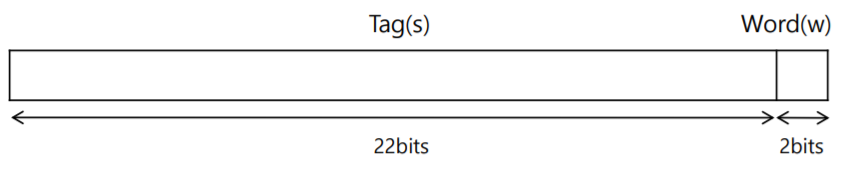
- Main Memory의 주소에서 Tag의 비트수는?
세트 연관 사상
- 직접 사상과 연관 사상의 장점을 취하고 단점을 줄이기 위한 절충안이다.
- 캐시는 여러 개의 세트들로 나누어지며, 각 세트들은 여러 개의 라인들로 구성된다.
- 세트: 캐시를 여러 개로 쪼갠 것
- v 연관 사상 캐시
- ‘v 연관 사상 캐시’는 ‘세트 연관 캐시’의 일종이다.
- 물리적으로 v개의 연관 캐시들로 구현할 수 있다.
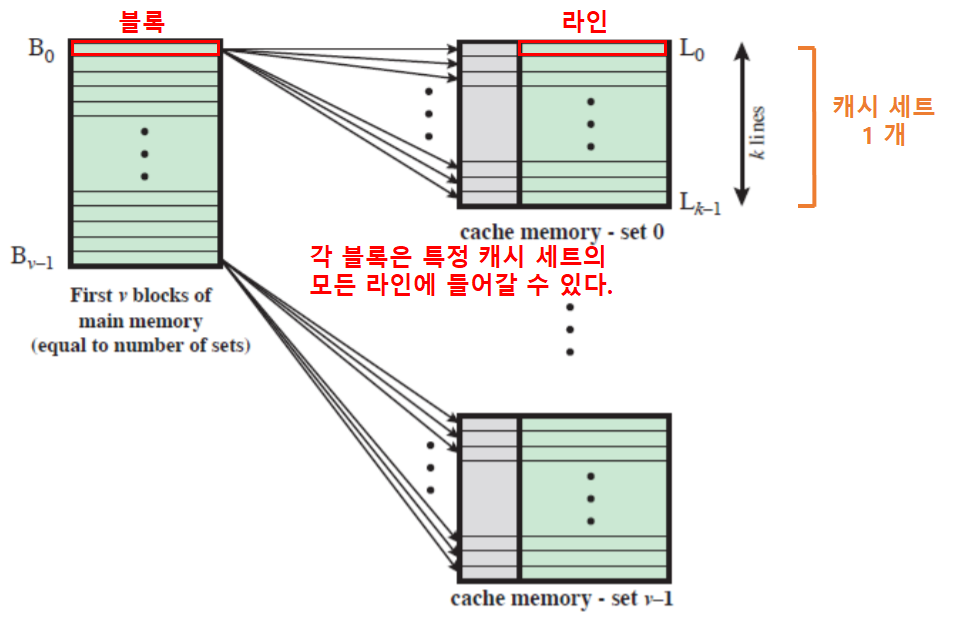
- k 직접 사상 캐시
- ‘k 직접 사상 캐시’는 ‘세트 연관 캐시’의 일종이다.
- k 개의 직접 사상 캐시들로 구현할 수 있다.
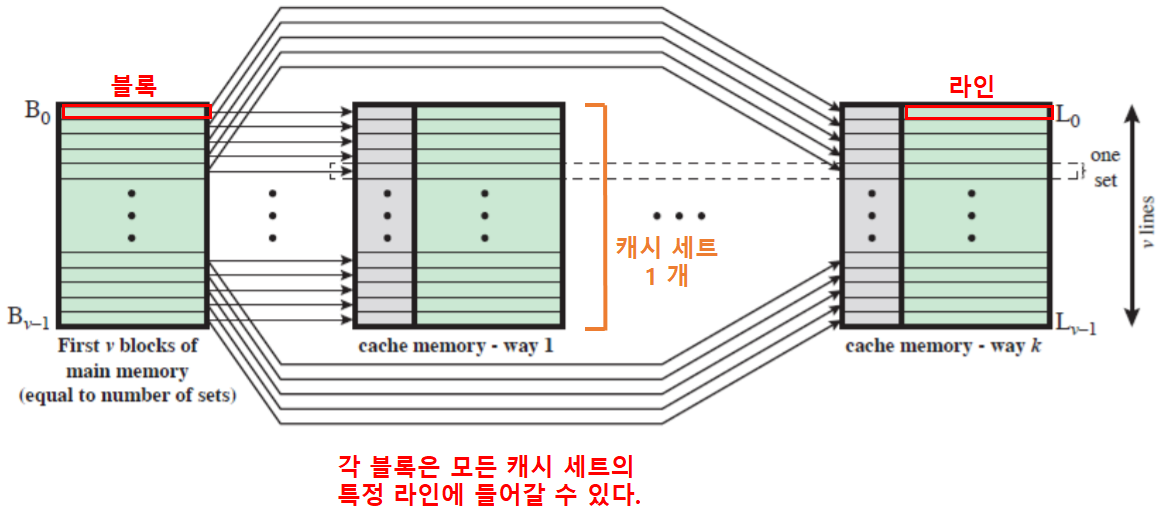
- 극단적으로 캐시를 쪼개어, 결국 모든 블록이 모든 라인에 갈 수 있다면 ⇒ 연관사상
-
Cache와 Main Memory 관계
세트 연관 사상: 예시 문제
- 가정
- Cache 크기 = 64KBits
- Main Memory 크기 = 16MBits
- Word 크기 = 1Bits
- Block 크기 = 4Bits
- 문제
- Main Memory의 주소에서 Tag의 비트수는?
- 연관 사상에서 Tag는 각 블록 집합을 구분하는 구분자이다. 따라서, 블록 집합의 개수만큼 표현할 수 있는 비트 개수가 필요하다.
- Tag 비트수 =
(블록집합 개수) =
(M.M크기/블록집합크기) =
비트
- Main Memory의 주소에서 Set 주소의 비트수는?
- Set 주소는 이미 특정된 블록 집합 내의 Block(Set, Line)들을 구분한다. 따라서, 블록 집합 내의 Block 개수만큼 표현할 수 있는 비트 개수가 필요하다.
- Set 비트수 =
(블록 집합당 Block 개수) =
(블록집합 크기/Block크기) =
비트
- Main Memory의 주소에서 Word 주소의 비트수는?
- Word 주소는 이미 특정된 블록 내의 Word들을 구분한다. 따라서, 블록 내의 Word 개수만큼 표현할 수 있는 비트 개수가 필요하다.
- Word 주소 비트수 =
(블록당 Word 개수) =
(블록크기/Word크기) =
(4B/1B) =
비트
- M.M (Main Memory)의 주소의 구성
- Tag길이 + Set(Block, Line)주소길이+ Word주소길이 = M.M의 주소 길이
- 9 + 13 + 2 = 24 비트

- Tag는 블록집합을 구분하고, 블록집합은 캐시 세트의 크기가 작을수록 많아진다.
- Set은 블록을 구분하고, 블록(Set)은 캐시 세트의 크기가 작을수록 작아진다.
- 따라서, 캐시가 쪼개짐에 따라 ‘Tag의 길이’와 ‘Set주소길이’가 변화한다.
- Main Memory의 주소에서 Tag의 비트수는?
캐시 크기에 대한 여러 연관성
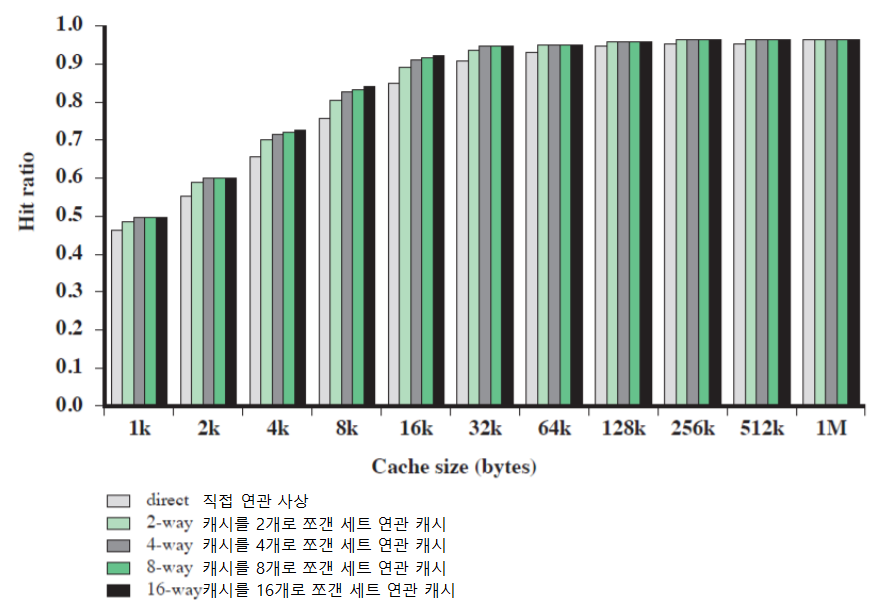
캐시 세트 크기에 따른 Hit율
교체 알고리즘
교체 알고리즘이란?
- 캐시가 채워진 뒤에, 새로운 블록을 캐시로 가져올 때 현재 캐시에 저장되어 있는 블록들 중의 하나는 반드시 교체되어야하는데, 이때 사용되는 알고리즘이다.
- 즉, 교체 알고리즘은 캐시 Miss시 블록 교체에 사용되는 알고리즘이다.
각 사상 방법에 따른 교체 알고리즘
- 직접 사상
- 직접 사상은 각 블록의 Line 위치가 정해져있으므로, 교체 알고리즘이 필요없다.
- 연관, 세트연관 사상
- 최소 최근 사용 (LRU: Least Recently Used)
- 사용되지 않은 채로 가장 오래 있었던 블록을 교체한다.
- 완전 연관 캐시를 비교적 쉽게 구현하게 한다.
- 최고의 적중률을 보이며, 가장 널리 사용된다.
- 선입선출 (FIFO: First In First Out)
- 캐시 내에 가장 오래 머물렀던 블록을 교체한다.
- 라운드 로빈, 원형 버퍼 기법 등으로 구현한다.
- 최소사용빈도 (LFU: Least Frequently Used)
- 가장 적게 참조되었던 블록을 교체한다.
- 각 라인에 카운터를 둔다.
- 임의 (Random)
- 사용횟수에 근거한 알고리즘보다 성능이 약간 낮다.
- 사용하지 못할 정도의 성능은 아니다.
- 최소 최근 사용 (LRU: Least Recently Used)
쓰기 정책
쓰기 정책의 필요성
- 주기억장치와 캐시 사이의 데이터의 일관성이 유지되어야 한다.
- 데이터 일관성을 지킬 수 있도록 하는 것이 바로 쓰기 정책이다.
- 데이터의 일관성?
- 장치 A와 장치 B의 데이터 값이 일치하도록 유지하는 것
쓰기 정책의 종류
- 연속 기록 방식
- 모든 쓰기 동작들이 캐시 뿐만 아니라, 주기억장치로도 동시에 행해진다.
- 즉, 데이터를 쓸때마다 Main Memory의 데이터를 갱신한다.
- 구조가 간단하지만, 매번 느린 주기억장치를 함께 액세스해야 하므로 성능이 떨어진다.
- 후 기록 방식
- 데이터의 갱신은 캐시에서만 일어난다. 그리고 해당 블록이 교체될 때 주기억장치를 갱신한다.
- 구조가 복잡하며, 주기억장치의 일부분이 무효 상태가 될 수 있다. (즉, 데이터 불일치 문제 발생 가능)
- CPU 기계 사이클이 IDLE 상태일때, 캐시의 내용을 주기억장치에 블록단위로 수시로 백업하면 시스템 성능을 높일 수 있다.
라인 크기
캐시에 저장되는 방식
- 한 개의 데이터 블록이 읽혀져서 캐시에 저장될 때, 원하는 단어 뿐만 아니라 인접한 몇개의 단어들이 같이 읽혀온다.
블록 크기가 증가할수록
- 지역성의 원리에 의해 적중률이 처음에는 증가한다.
- 블록이 더 커지면, “새로 인출된 정보가 사용될 확률”이 “교체되어야 하는 정보를 다시 사용하게 될 확률”보다 더 낮아져서 적중률이 감소할 수 있다.
- 즉, 블록이 너무 커서 현재 잘 사용 중인 Word가 바뀌어 버릴 가능성이 높아진다.
블록 크기와 적중률 간의 관계
- 블록이 커질수록 캐시에 들어올 수 있는 블록의 수는 감소한다.
- 블록의 수가 감소하면, Word가 인출된 직후에 다른 블록과 다시 교체된다.
- 블록이 커질수록, 원하는 단어로부터 멀리 떨어져있는 단어들도 같이 읽혀오며, 그들이 가까운 미래에 사용될 가능성은 낮다.
- 지역성의 원리가 적용되지 않는 범위까지 가져와버리기 때문이다.
- 따라서, 8~64Bits 가 캐시 크기의 최적이다.
캐시의 개수
다단계 캐시
- 온 칩 캐시 (On-chip, 내부캐시, L1캐시)
- processor 내부에 위치한다.
- 프로세서의 외부 활동을 줄여주며, 실행시간을 가속시키고 전체 시스템 성능을 향상시킨다.
- 오프 칩 캐시 (Off-chip, 외부캐시, L2캐시)
- SRAM을 사용하며 DRAM보다 빠르다.
- L2 캐시와 프로세서 사이에 별도의 데이터 버스를 이용한다.
- L2 버스도 프로세서 칩에 포함시키고 있는 추세이며, L3 캐시도 등장했다.
-
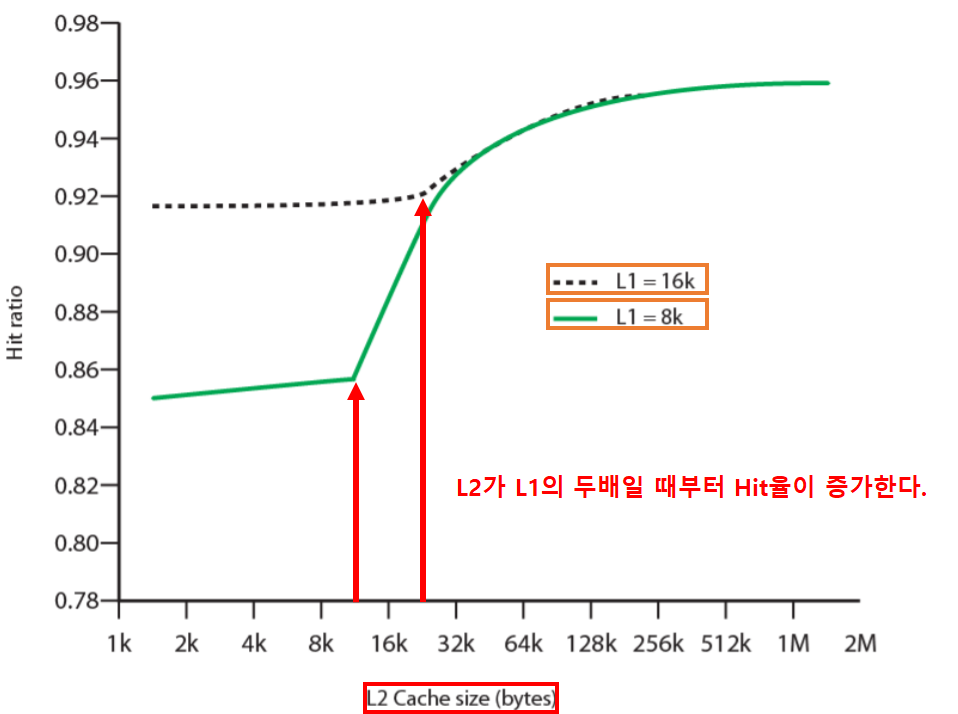
L2 캐시는 L1 캐시 크기의 두배가 될때까지는 캐시 Hit율에 영향력이 없다.
분리캐시
- “명령어 전용 캐시” 와 “데이터 전용 캐시” 로 구성된다.
- 명령어 인출/해독 유니트와 실행 유니트 간에 캐시로 인한 경합이 없다.
- 명령어 파이프라인 구조에서 유리하다.
- 파이프라인: 프로세서가 쉬지않고 계속 일하게끔 하는 방법 중 하나 (추후에 상세설명 예정)
- 일반적으로 분리 캐시를 채택하고 있다.
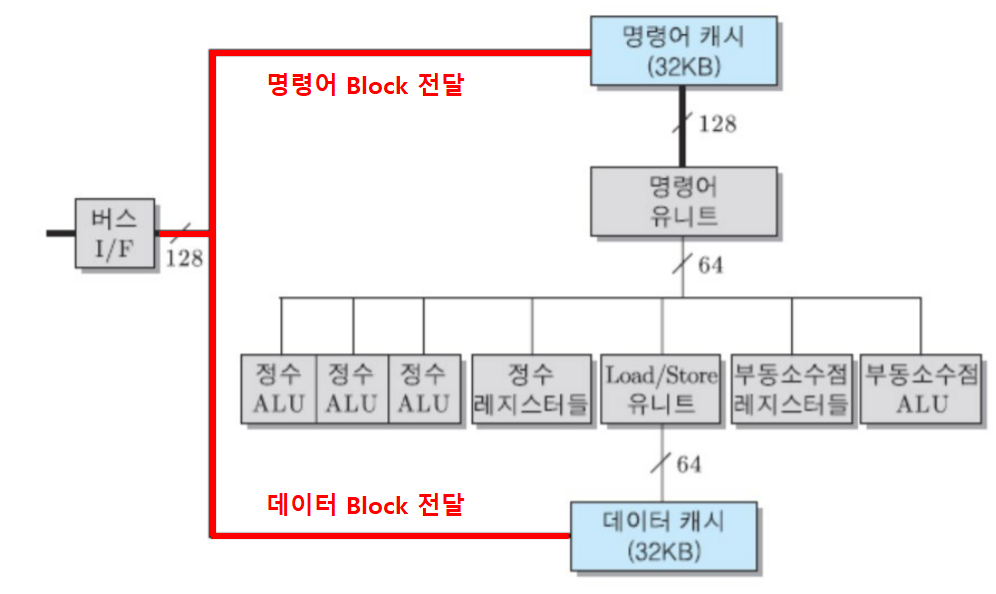
통합 캐시
- 통합 캐시는 “명령어 캐시”와 “데이터 캐시”의 구분이 없는 것이다.
- 주어진 캐시 크기에 대해서는, 통합 캐시가 분리 캐시보다 적중률이 높다.
- 명령어와 데이터 간의 균형이 자동적으로 유지된다.
- 명령어 캐시가 꽉 차고 데이터 캐시에 여유가 있는 경우, 분리 캐시는 빈 공간 활용에 제약이 있다.
- 왜냐하면, 데이터 캐시가 비어있다고 해당 자리에 명령어를 저장할 수 없기 때문이다.
- 즉, 통합 캐시는 공간 효율성이 분리캐시보다 더 좋다.
- 명령어 캐시가 꽉 차고 데이터 캐시에 여유가 있는 경우, 분리 캐시는 빈 공간 활용에 제약이 있다.
- 파이프라인 구조, 병렬처리 구조에서는 분리캐시가 더 유리하다.
캐시 조직의 예시
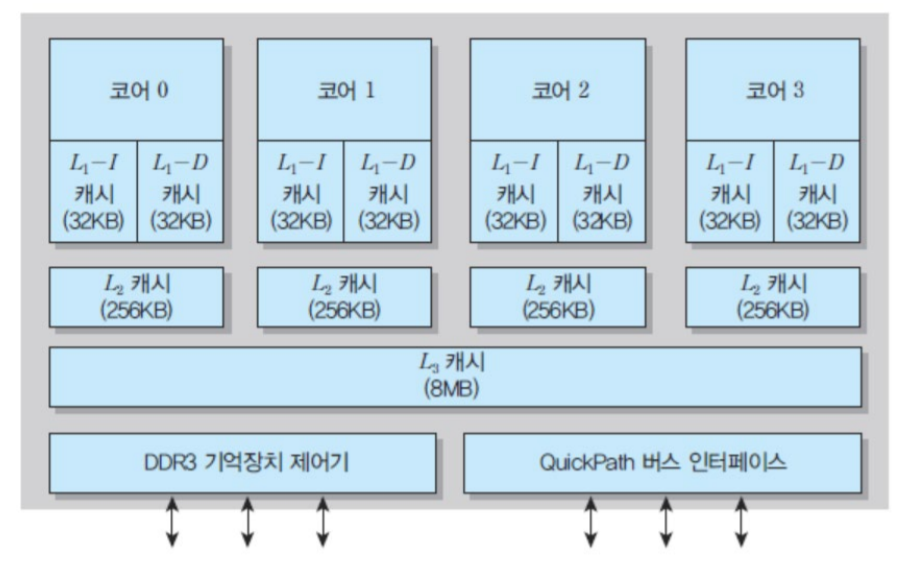
- 코어당 L1 캐시가 2개 존재한다. ⇒ 명령어 전용 캐시, 데이터 전용 캐시가 존재한다.
- L3 캐시를 각 코어가 공유한다.
- 성결대학교 컴퓨터 공학과 최정열 교수님 (2021)
- William Stalling, 『컴퓨터시스템구조론(10판)』
