트리
개요
트리란?
- 계층적인 구조를 나타내는 자료구조
- 부모-자식 관계의 노드들로 이루어짐
용어 총정리
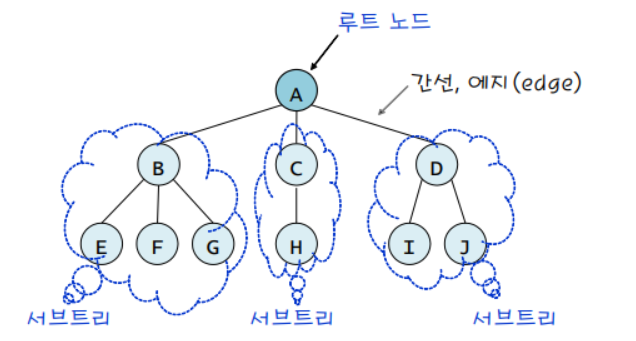
- 노드
- 트리의 구성요소
- 루트
- 부모가 없는 노드
- 서브 트리
-
하나의 노드와 자손들로 이루어짐
-
- 단말 노드
- 자식이 없는 노드
- 비단말 노드
- 자식을 가지는 노드
- 간선, 엣지
- 연결선
- 자식
- 직계 자손
- 부모
- 직계 조상
- 형제
- 같은 부모를 갖는 노드 관계
- 조상
- 자손
- 차수
- 어떤 노드의 자식 노드의 수
- 트리의 차수
- 트리가 가지고 있는 노드의 차수 중 가장 큰 값
- 레벨
- 트리의 각 층의 번호
- 루트노드는 레벨1이다.
- 높이
- 트리의 최대 레벨
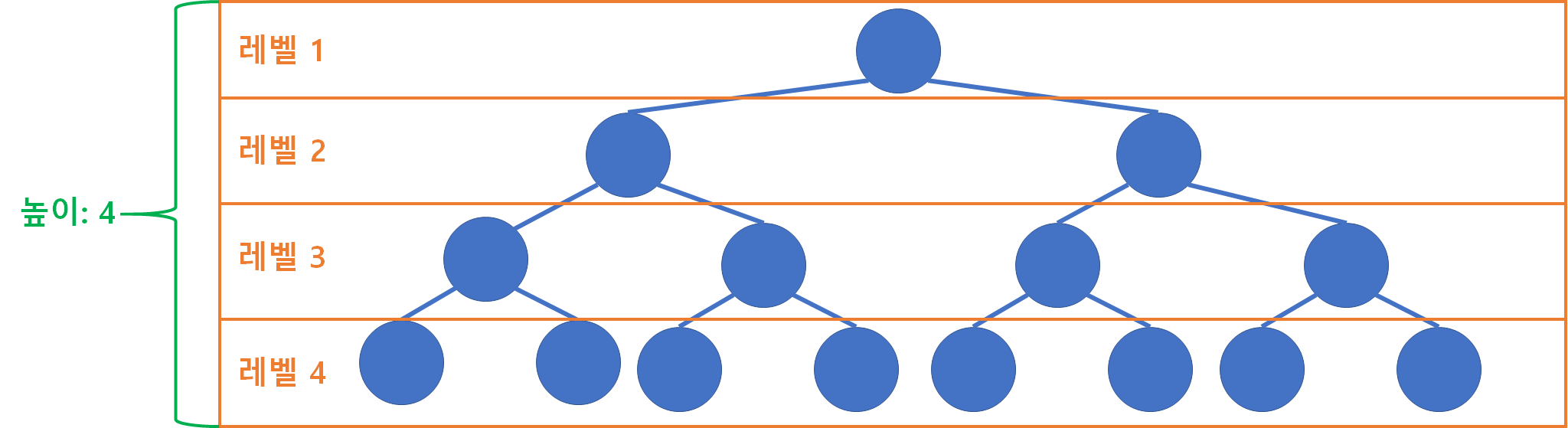
- 트리의 최대 레벨
- 포레스트
- 여러 개의 트리의 집합
일반 트리 표현
배열활용
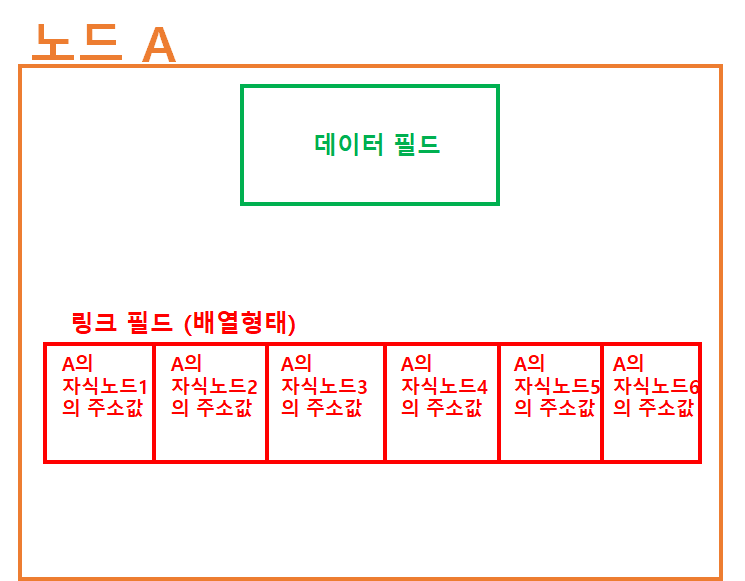
- 노드 구조를 이용
- 데이터 필드와 링크 필드 존재
-
링크 필드: 배열형태
배열로 구현된 링크필드:
각 요소가 해당 노드의 자식을 각각 의미함 (링크필드의 길이 == 노드의 차수)노드마다 배열의 길이가 달라짐 (자식의 개수가 다르므로)
연결 리스트 활용
- 노드 구조를 이용
- 데이터 필드
- 링크 필드 1: 연결 리스트 형태, 현 노드의 첫 번째 자식노드
- 링크 필드 2: 연결 리스트 형태, 현 노드의 오른쪽 형제노드
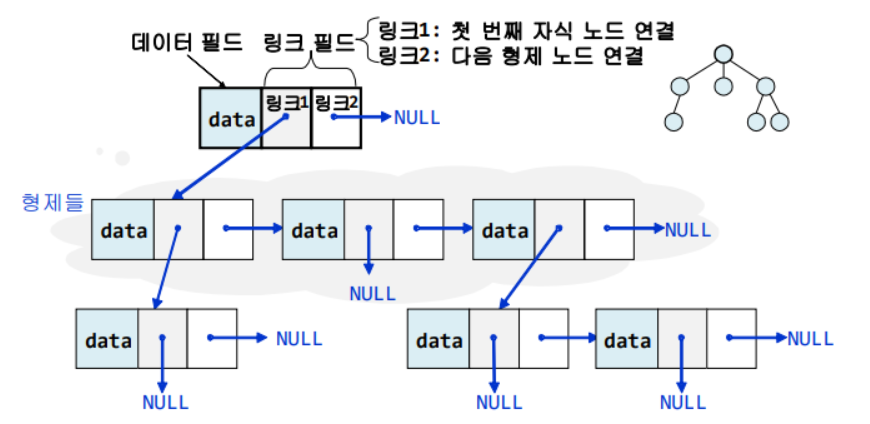
하지만 너무 복잡하다.
이진 트리
이진 트리란?
- 모든 노드가 최대 두 개의 서브트리를 가지고 있는 것
- 모든 노드의 차수가 2이하
- 자식들간(서브 트리)의 순서가 존재 (왼쪽, 오른쪽)
이진 트리 성질
- 노드의 개수가 n개일때,
간선의 개수는 n-1개이다. - h: 높이 일 때,
최소 h개~최대 2^h-1개의 노드를 가짐-
노드개수가 최소인 경우
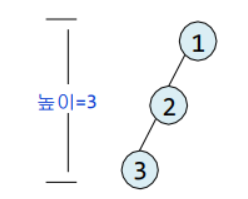
-
노드개수가 최대인 경우
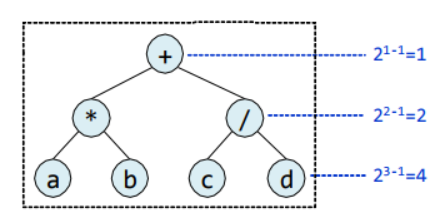
-
- n: 노드개수 일 때,
ceiling(log_2(n+1))이상 n이하의 높이를 가짐
이진트리 분류
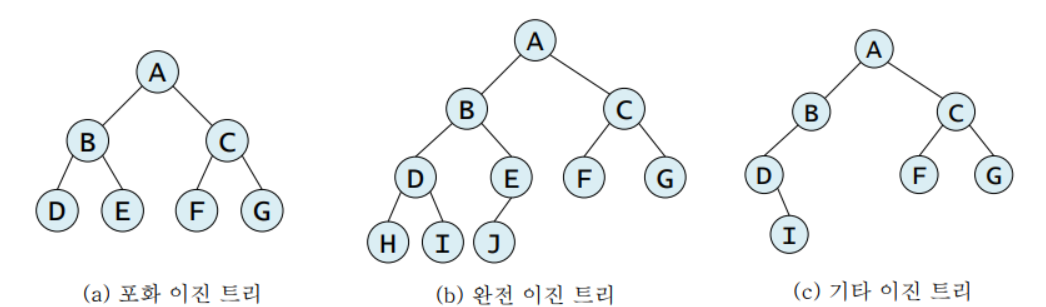

포화 이진 트리
포화 이진 트리란?
- 트리의 각 레벨에 노드가 꽉 차있는 이진 트리
특징
- 높이가 k이고 노드 개수가 n일 때, n = 2^k-1
노드 번호
- 레벨 단위로 왼쪽에서 오른쪽으로 순서대로 번호를 붙임
- 번호는 항상 일정하다 (루트노드의 오른쪽 자식노드의 번호 == 항상 3)
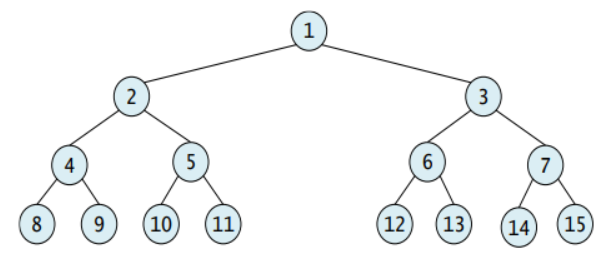
완전 이진 트리
완전 이진 트리란?
- 높이가 h일 때, 레벨1 ~ 레벨(h-1) 까지는 노드가 모두 채워짐
- 마지막 레벨 h에서는 노드가 순서대로 채워짐 (중간에 빈 곳이 있으면 안됨)
노드 번호
- 포화 이진트리와 동일
예시
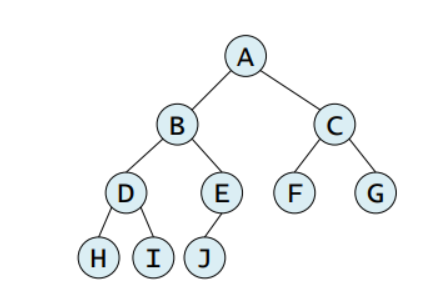
이진 트리의 추상 자료형
데이터 (전체 이진트리의 데이터)
- 노드의 집합
- 공집합
- 루트 노드
- 왼쪽 서브 트리
- 오른쪽 서브 트리
(모든 서브 트리는 이진트리이어야 함)
연산
- init()
- 이진 트리 초기화
- is_empty()
- 이진 트리가 공백 상태인지 확인
- create_tree( e, left, right )
- 이진 트리 left와 right를 자식노드로,
- e를 루트로 하는 이진 트리 생성
- get_root()
- 이진 트리의 루트 노드를 반환
- get_count()
- 이진 트리의 노드의 수를 반환
- get_leaf_count()
- 이진 트리의 단말 노드의 수를 반환
- get_height()
- 이진 트리의 높이 반환
이진 트리 표현: 배열
-
포화 이진 트리 or 완전 이진 트리 or 일반 이진 트리 표현가능
-
표현 예시
- 전제
- 완전트리
- 높이에 따라 배열의 길이 결정
-
높이 k: 길이가 2^k-1인 배열이 필요
완전 이진 트리가 최대로 가질 수 있는 노드 수 = 포화 이진 트리의 노드 수
- 표현법
- 각 노드에 번호를 붙여서 그 번호를 배열의 인덱스로 삼아 노드의 데이터를 배열에 저장
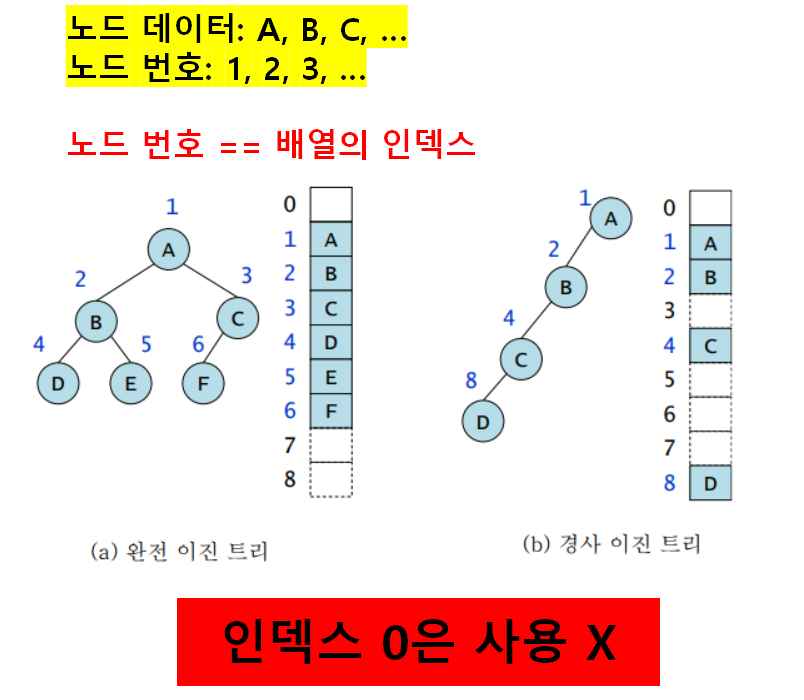
- 각 노드에 번호를 붙여서 그 번호를 배열의 인덱스로 삼아 노드의 데이터를 배열에 저장
- 전제
- 특징
- 어떤 노드의 인덱스를 알면, 그 노드의 부모나 자식 인덱스 계산 가능
be) 노드의 번호 == 배열 인덱스
- 어떤 노드의 인덱스를 알면, 그 노드의 부모나 자식 인덱스 계산 가능
- 노드 i의 부모 노드 인덱스
- i가 왼쪽 자식일 때: i/2
- i가 오른쪽 자식일 때: floor(i/2)
- 노드 i의 왼쪽 자식 노드 인덱스
- 2*i
- 노드 i의 오른쪽 자식 노드 인덱스
- 2*i + 1
-
문제점
- 기억 공간 낭비
- 배열의 크기에 따라 트리의 높이 제한
이진 트리 표현: 링크
- 부모 노드가 자식 노드를 가리키게 함 (with 포인터)
-
주요 표현법
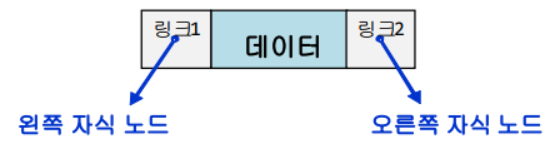
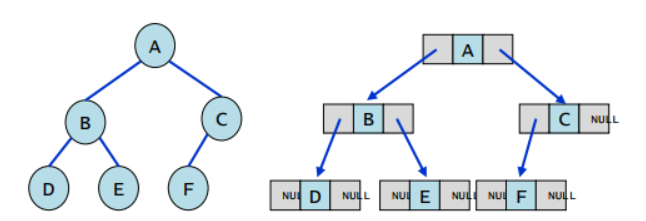
이진트리 구현 - 링크 이용
노드 구조체
typedef char TElement; //트리의 노드에 저장할 데이터 타입
//노드 구조체
typedef struct BinTrNode {
TElement data; //노드에 저장될 데이터
struct BinTrNode *left; //노드의 왼쪽 자식노드
struct BinTrNode *right; //노드의 오른쪽 자식노드
} TNode;
TNode *root = NULL; //루트노드를 가르킬 포인터 변수
init_tree()
void init_tree() {
root = NULL;
}
is_empty_tree()
int is_empty_tree() {
return root == NULL;
}
get_root()
TNode* get_root() {
return root;
}
create_tree(TElement value, TNode * left, TNode* right)
TNode* create_tree(TElement value, TNode * left, TNode* right) {
TNode *n = (TNode*)malloc(sizeof(TNode));
n->data = value;
n->left = left;
n->right = right;
return n;
}
전체 예시
typedef char TElement; //트리의 노드에 저장할 데이터 타입
//노드 구조체
typedef struct BinTrNode {
TElement data; //노드에 저장될 데이터
struct BinTrNode *left; //노드의 왼쪽 자식노드
struct BinTrNode *right; //노드의 오른쪽 자식노드
} TNode;
TNode *root = NULL; //루트노드를 가르킬 포인터 변수
void init_tree() {
root = NULL;
}
int is_empty_tree() {
return root == NULL;
}
TNode* get_root() {
return root;
}
TNode* create_tree(TElement value, TNode * left, TNode* right) {
TNode *n = (TNode*)malloc(sizeof(TNode));
n->data = value;
n->left = left;
n->right = right;
return n;
}
void main() {
TNode *b, *c, *d, *e, *f;
init_tree();
d = create_tree('D', NULL, NULL);
e = create_tree('E', NULL, NULL);
b = create_tree('B', d, e);
f = create_tree('F', NULL, NULL);
c = create_tree('C', f, NULL);
root = create_tree('A', b, c);
}
- 성결대학교 컴퓨터 공학과 박미옥 교수님 (2021)
- 최영규, 『두근두근 자료구조』
