큐
개요
특징
- 선입선출
큐 ADT
특징
- 삽입 : 큐의 후단(rear)
- 삭제 : 큐의 전단(front)
데이터
선입선출의 접근 방법을 유지하는 요소들의 모음
연산
- init() : 큐를 초기화한다.
- enqueue(e) : 주어진 요소 e를 큐의 맨 뒤에 추가
- dequeue() : 큐가 비어있지 않으면 맨 앞 요소를 삭제하고 반환한다.
- is_empty() : 큐가 비어있으면 true 큐가 비어있지 않다면 false
- peek() : 큐가 비어있지 않으면 맨 앞 요소를 삭제하지 않고 반환한다.
- is_full() : 큐가 가득 차 있으면 true 큐가 가득 차 있지 않다면 false
- size() : 큐의 모든 요소들의 개수 반환
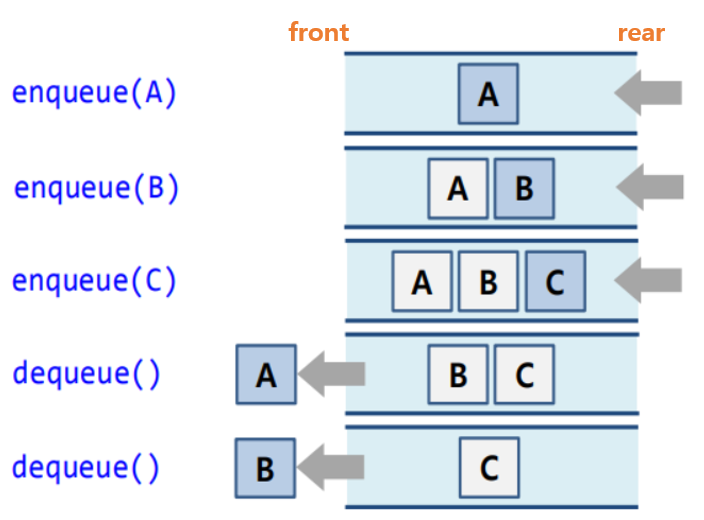
선형큐
특징
- 선형으로 큐를 구현
원리
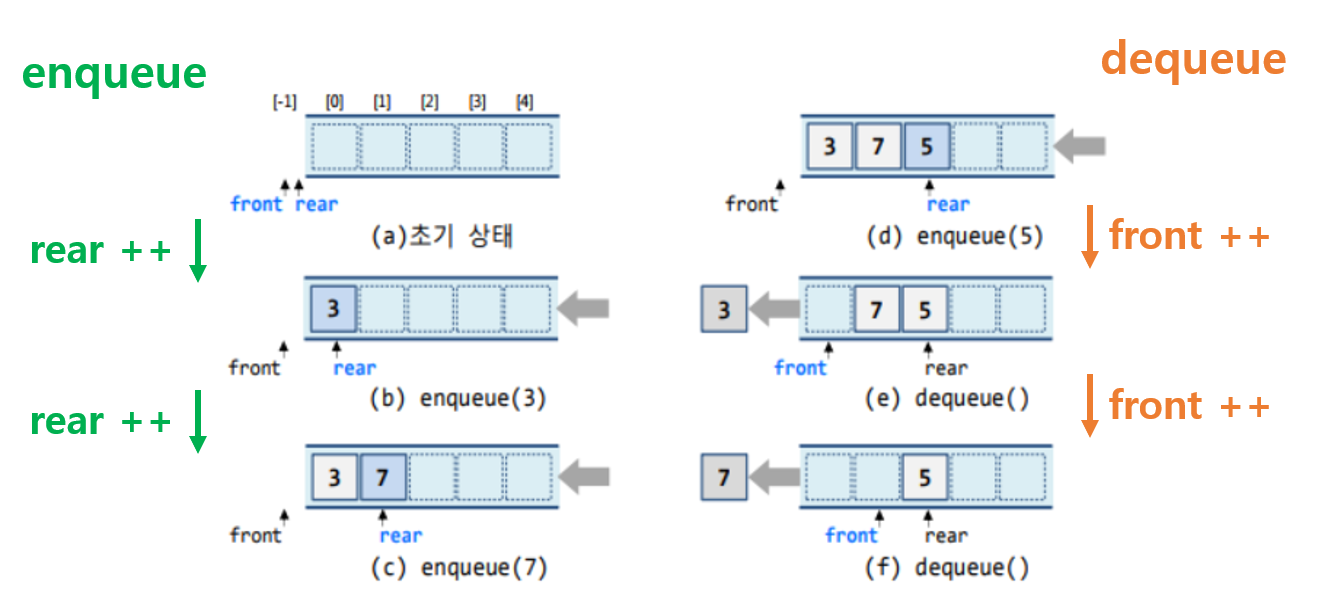
선형큐의 문제점
- 삽입을 계속하기 위해서는 요소들을 이동시켜야 함 (dequeue 할 때 마다)
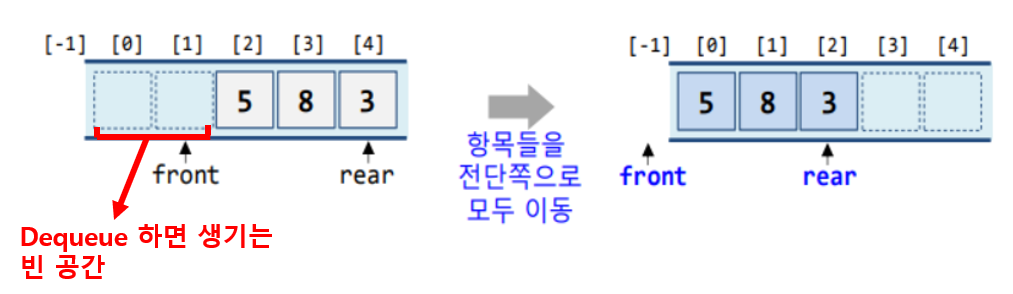
해결법 : 원형큐
원형 큐
구조
- front : 첫 번째 요소 하나 앞의 인덱스
- rear : 마지막 요소의 인덱스
원형 큐의 삽입 삭제 연산
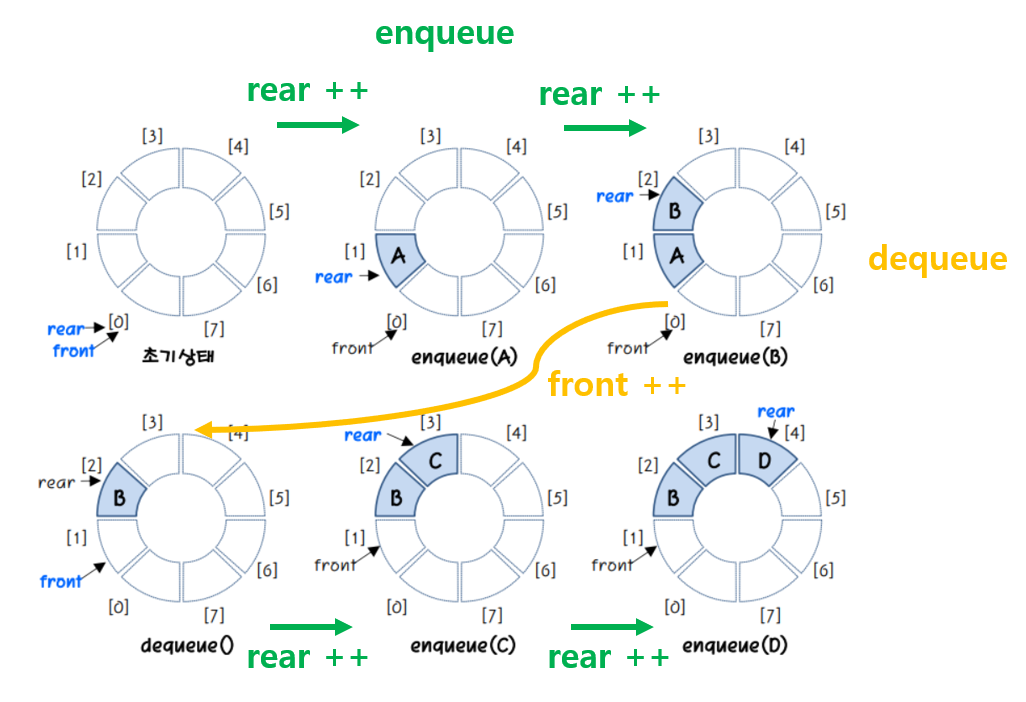
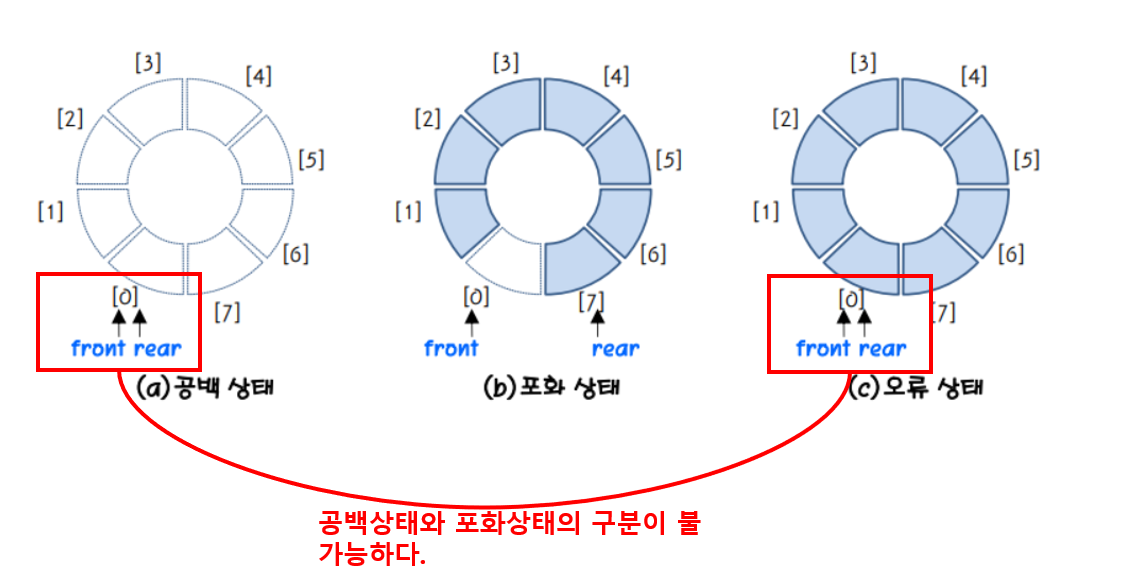
상태
- 공백상태
- front == rear
- 포화상태
- M : 원형큐의 최대크기
- front%M == (rear+1)%M
<문제점>
원형큐의 모든 공간에 요소가 있다면, "front == rear == 0"이 된다. 이것은 공백상태와 동일한 상태로, 포화상태와 공백상태의 구분이 불가능하다. ⇒ **해결책 : 하나의 공간은 남겨둔다.**
알고리즘
init() 연산
- 공백상태로 만드는 것
- front와 rear 동일한 값으로 설정
- 모두 0으로 초기화

size() 연산

<MAX_QUEUE_SIZE를 더한 뒤, 다시 MAX_QUEUE_SIZE로 나누는 이유>
rear<front 일때, 음수가 나오지 않게 하기 위해
is_empty() 연산

is_full() 연산

삽입(enqueue) 연산
- 나머지 연산을 사용하여 인덱스를 원형으로 회전시킨다. (index가 큐의 최대 크기를 넘지 못하도록)

삭제(dequeue) 연산
- 나머지 연산을 사용하여 인덱스를 원형으로 회전시킨다. (index가 큐의 최대 크기를 넘지 못하도록)

구현
초기변수설정
#define Element int
#define MAX_QUEUE_SIZE 100
Element data[MAX_QUEUE_SIZE];
int front;
int rear;
init()
void init() {
front = rear = 0;
}
is_empty()
int is_empty() {
return front==rear;
}
is_full()
int is_full() {
return front == (rear+1)%MAX_QUEUE_SIZE;
}
size()
int size() {
return (rear - front + MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE;
}
print_queue()
void print_queue(char msg[]) {
int i, maxi = rear;
if(front >= rear) {
maxi += MAX_QUEUE_SIZE;
}
printf("%s[%2d] = ", msg, size());
for(i=front+1; i<=maxi; i++) {
printf("%2d ", queue[i%MAX_QUEUE_SIZE]);
}
printf("\n");
}
삽입(enqueue)
void enqueue(Element val) {
if( is_full() ) {
error("큐 포화 에러");
}
rear = (rear+1) % MAX_QUEUE_SIZE;
queue[rear] = val;
}
삭제(dequeue)
Element dequeue() {
if( is_empty() ) {
error("큐 공백 에러");
}
front = (front+1) % MAX_QUEUE_SIZE;
return queue[front];
}
살펴보기(peek)
Element peek() {
if(is_empty()) {
error("큐 공백상태");
}
return queue[(front+1)%MAX_QUEUE_SIZE];
}
종합예제
#include <stdio.h>
#define Element int
#define MAX_QUEUE_SIZE 100
Element queue[MAX_QUEUE_SIZE];
int front;
int rear;
void init() {
front = rear = 0;
}
int size() {
return (rear-front+MAX_QUEUE_SIZE) % MAX_QUEUE_SIZE;
}
int is_full() {
return front == (rear+1)%MAX_QUEUE_SIZE;
}
int is_empty() {
return front == rear;
}
void enqueue(Element e) {
if(is_full()) {
error("큐 포화상태");
}
rear = (rear+1) % MAX_QUEUE_SIZE;
queue[rear] = e;
}
Element dequeue() {
if(is_empty()) {
error("큐 공백상태");
}
front = (front+1)%MAX_QUEUE_SIZE;
return queue[front];
}
Element peek() {
if(is_empty()) {
error("큐 공백상태");
}
return queue[(front+1)%MAX_QUEUE_SIZE];
}
int main() {
init();
int i;
for(i=0; i<10; i++) {
enqueue(i);
}
for(i=0; i<112; i++) {
printf("dequeue : %d\n", dequeue());
}
}
- 성결대학교 컴퓨터 공학과 박미옥 교수님 (2021)
- 최영규, 『두근두근 자료구조』
