B Tree & B+ Tree
B Tree
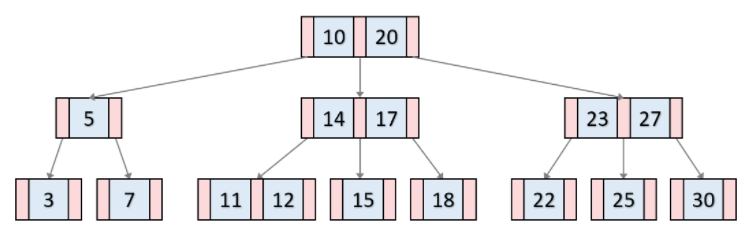
B Tree 란?
- 데이터베이스, 파일 시스템에서 널리 사용되는 트리 자료구조의 일종이다.
- 이진 트리를 확장해서, 더 많은 수의 자식을 가질 수 있게 일반화시킨 것이 B-Tree 이다.
- B-Tree 는 다차원 트리이다.
- 즉 B Tree 는 모든 리프노드들이 같은 레벨을 가지도록 자동으로 균형을 맞추는 트리이다.
- 하나의 노드에 많은 수의 데이터를 저장할 수 있다.
특징
-
자식 수에 대한 일반화를 진행하면서, 하나의 레벨에 더 저장되는 것 뿐만 아니라 트리의 균형을 자동으로 맞춰주는 로직까지 갖추었다.
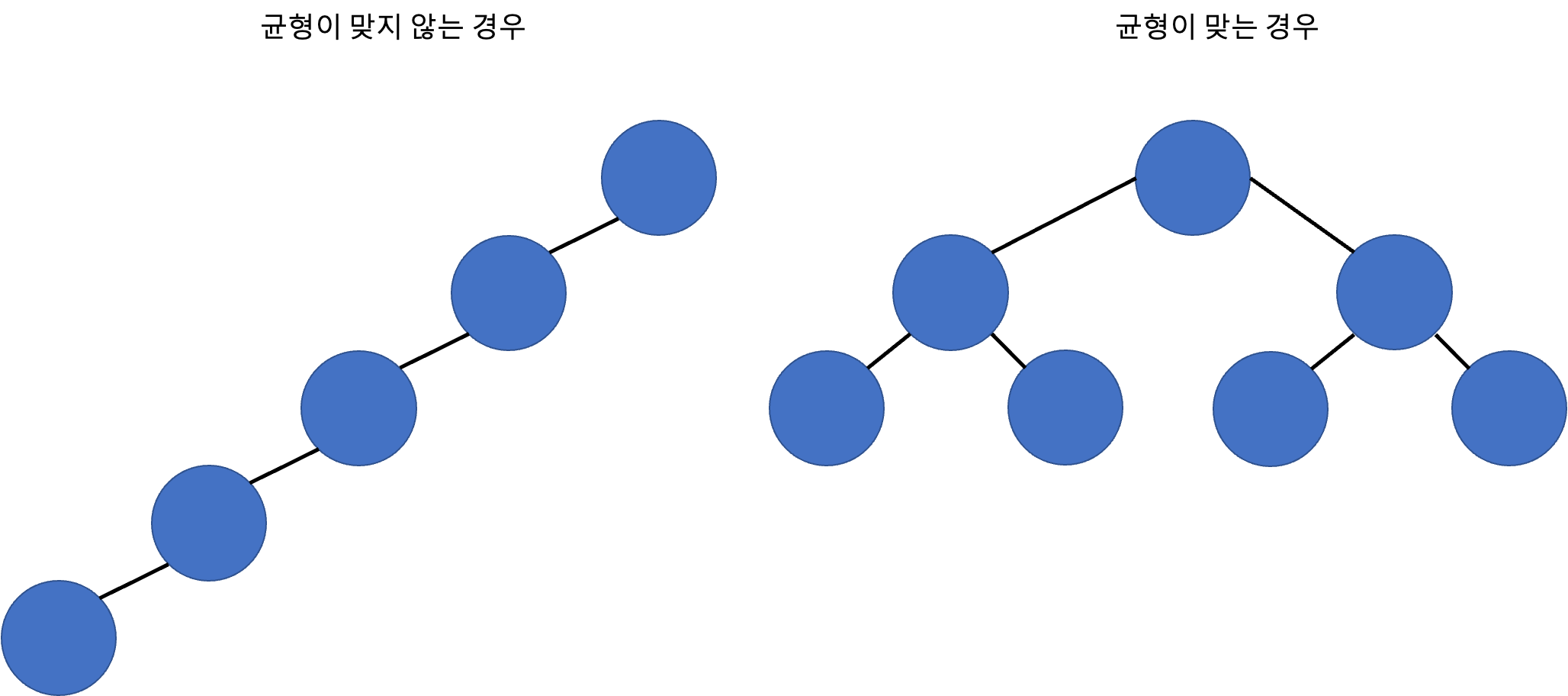
- 레벨로만 따지면 완전히 균형을 맞춘 트리이다.
- 리프 노드가 모두 같은 레벨에 존재한다.
- 하나의 노드에 많은 수의 데이터를 저장할 수 있다.
-
각 노드에는
key와data pointer가 존재한다.파일 시스템에서 사용되는 B Tree를 예로 든다면 아래와 같다.
key: 파일명data pointer: 실제 파일이 저장된 하드디스크의 블록 번호 (주소)
- 검색 시 시간복잡도는 항상 O(logN) 이다.
- root가 아닌 노드들은 최소
M/2개, 최대M개의 자식노드를 가지고 있다. (리프노드라면 0개)- 3차 B Tree : 최소
1(3/2)개, 최대3개의 자식노드 - 4차 B Tree : 최소
2(4/2)개, 최대4개의 자식노드
- 3차 B Tree : 최소
- 한 노드에는 최소
(M/2) - 1개의 키(데이터), 최대M-1개의 키(데이터)가 포함될 수 있다.- 3차 B Tree : 최소
0(3/2-1)개, 최대3개의 키를 한 노드에서 가짐 - 4차 B Tree : 최소
2(4/2 - 1)개, 최대4개의 키를 한 노드에서 가짐
- 3차 B Tree : 최소
장점
- 노드들의 균형이 맞춰져 있어, 검색속도가 항상
O(logN)이다.- 편향된 이진 트리의 경우, 최악의 경우 검색속도가
O(N)이다.
- 편향된 이진 트리의 경우, 최악의 경우 검색속도가
- 대량의 데이터를 처리해야 할 때, 하나의 노드에 많은 데이터를 가질 수 있다는 점은 상당히 큰 장점이다.
- 왜냐하면 대량의 데이터는 메인 메모리가 아닌, 하드디스크 or SSD에 저장하기 때문이다.
- 하드디스크 or SSD : 블럭 단위로 입출력 수행
- 예를 들어 한 블럭의 크기가 1024 바이트라고 할 때, 2 바이트를 읽으려고 하거나 1024 바이트를 읽으려고 할 때 발생하는 비용은 같다.
- 따라서 하나의 노드를 1024 바이트로 꽉 채울 수 있다면, 입출력에 있어 효율적이다.
- 하나의 블럭만 가져와도, 해당 노드의 데이터를 블럭 교체없이 읽을 수 있으므로
규칙
- 노드의 자료수가 N이면, 자식 수는 N+1이어야 한다.
- 각 노드의 자료는 정렬된 상태여야 한다.
- 루트 노드는 적어도 2개 이상의 자식을 가져야 한다.
- 루트 노드를 제외한 모든 노드는 적어도 M/2개의 자료를 가지고 있어야 한다.
- 외부 노드로 가는 경로의 길이는 모두 같다.
- 입력 자료는 중복될 수 없다.
검색 연산

3차 B-Tree에서 17을 찾는 과정
루트노드에서부터 하향식으로 검색을 수행한다.
- 루트노드에서 시작해, 각 노드마다 저장된 key들을 순회하면서 비교한다.
- k(검색할 key)와 같은 key를 찾았다면 검색을 종료한다.
- k와 key들의 대소관계를 비교한다. 어떤 key들 사이에 k가 속한다면 해당 key들 사이의 자식노드로 넘어간다.
- 이 과정을 리프노드에 도달할 때까지 반복한다. 만약 리프노드에도 k와 동일한 key가 없다면 검색 실패로 처리한다.
삽입 연산
삽입할 위치를 찾기 위해, 트리를 탐색하는 과정은 위와 동일하다.
-
분할이 일어나지 않는 경우

3차 B-Tree에 20을 삽입하는 과정
- 리프노드가 가득차지 않았다면, 해당 노드에 오름차순으로 k(삽입할 key)를 삽입한다.
-
분할이 일어나는 경우

3차 B-Tree에 19를 삽입하는 과정
- 리프노드가 가득 차있다면, 중앙값을 기준으로 분할을 수행한다.
- 중앙값을 부모 노드의 key값으로 올리고, 중앙값 기준 좌, 우 값을 자식노드로 변환한다.
- 위 과정을 재귀적으로 수행해서, 부모의 key 개수가 차수 미만(M-1)임을 만족하면 종료한다.
삭제 연산
-
리프노드의 Key값을 지우는 경우

3차 B-Tree에서 18을 삭제하는 과정
- 만약 key가 여러개인 리프노드의 key를 지우는 경우, 그냥 지우면 된다.

3차 B-Tree에서 19를 삭제하는 과정
- 만약 key가 하나뿐인 리프노드의 key를 지우는 경우, 삭제한 노드의 부모 노드와 형제 노드를 merge 한다.
- 이 작업을 재귀적으로 B-Tree 구조를 만족할 때까지 반복한다.
-
리프노드가 아닌 key 값을 지우는 경우

3차 B-Tree에서 11을 삭제하는 과정
- 해당 노드에서 key값을 삭제하고, 왼쪽 서브트리의 key들 중 최댓값(리프노드임)을 노드의 key값으로 위치 시킨다.
- 삭제할 key값의 바뀐 위치(기존에 왼쪽 서브트리의 key들 중 최댓값이 있던 위치)의 k를 제거한다.
- 그리고 위 case들(리프노드의 key를 제거하는 경우)의 과정을 수행한다.
## B+ Tree
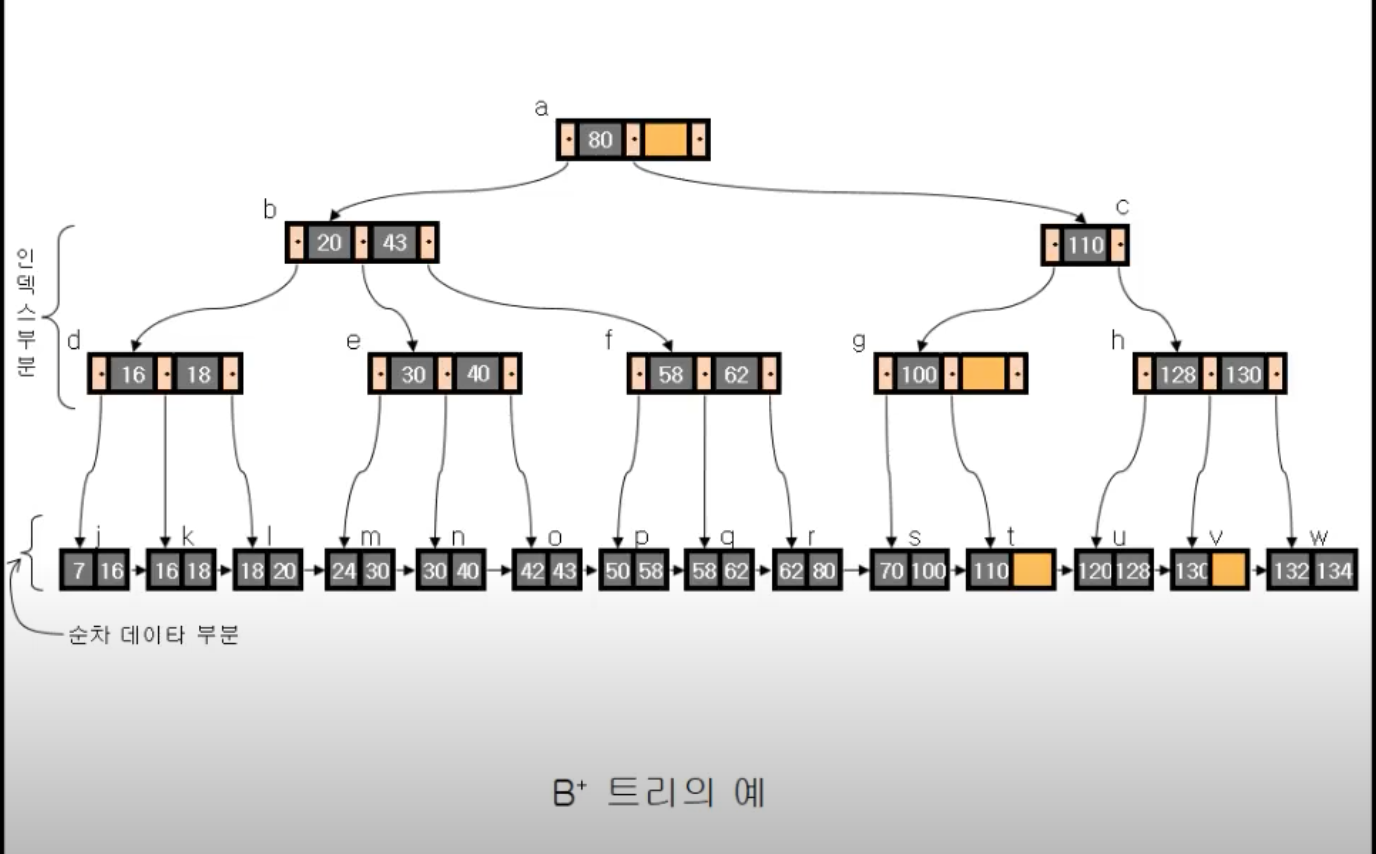
B+ Tree
B+ Tree 란?
- 데이터의 빠른 접근을 위한 인덱스 역할만 하는
비단말 노드 (Not Leaf)가 추가로 있다.- 기존의 B-Tree와 데이터의 연결리스트로 구현된 색인구조
- B-Tree의 변형 구조로,
index 부분과리프노드로 구성된 순차 데이터 부분으로 이루어진다.- 즉 모든 key들은 리프노드에 위치해 있고, 비단말 노드들은 리프노드에 위치한 key를 찾기 위한 index로 사용된다.
- 인덱스 부분의 key 값은 리프노드에 있는 key 값을 직접 찾아가는데 사용한다.
특징
- 데이터노드 (리프노드) 는 연결리스트로 형성되어있다.
- 데이터노드 하나의 크기는 인덱스노드 (비단말노드) 하나의 크기와 똑같지 않아도 된다.
-
리프노드만 데이터노드 역할을 하므로, 리프노드에는
key와data pointer가 저장되고, 비단말노드에는key만 저장된다.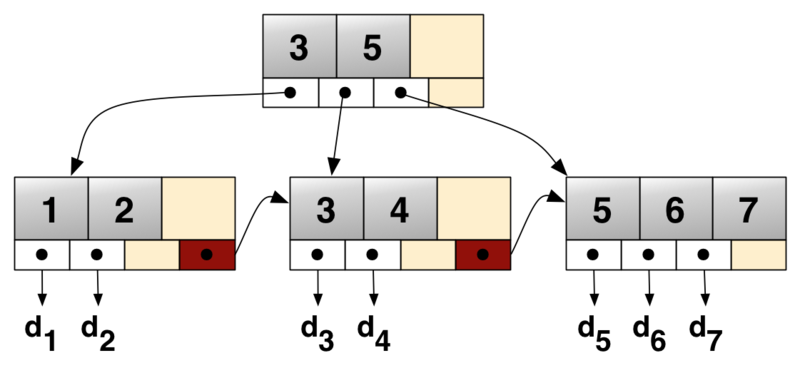
dn은 디스크의 주소를 가르킨다.
장점
- B+ 트리의 높이는 B 트리보다 낮게 구성되므로, 검색시간과 디스크 접근 횟수가 줄어든다.
- 블럭 사이즈를 더 많이 이용할 수 있다.
- B 트리의 경우, 모든 노드가 데이터노드이다. 따라서 모든 노드는
key와데이터의 주소를 저장해야 한다. - B+ 트리는 리프노드만 데이터노드 역할을 한다. 따라서 비단말노드에는
key만 저장해도 된다.
- B 트리의 경우, 모든 노드가 데이터노드이다. 따라서 모든 노드는
- 리프노드끼리 연결 리스트로 연결되어 있기 때문에, 범위 탐색에 매우 유리하다.
단점
- B Tree 의 경우 탐색 시 최상의 케이스에선 루트에서 끝날 수 있지만, B+ Tree는 무조건 리프노드까지 내려가봐야 한다.
B-Tree vs B+Tree
노드의 구성
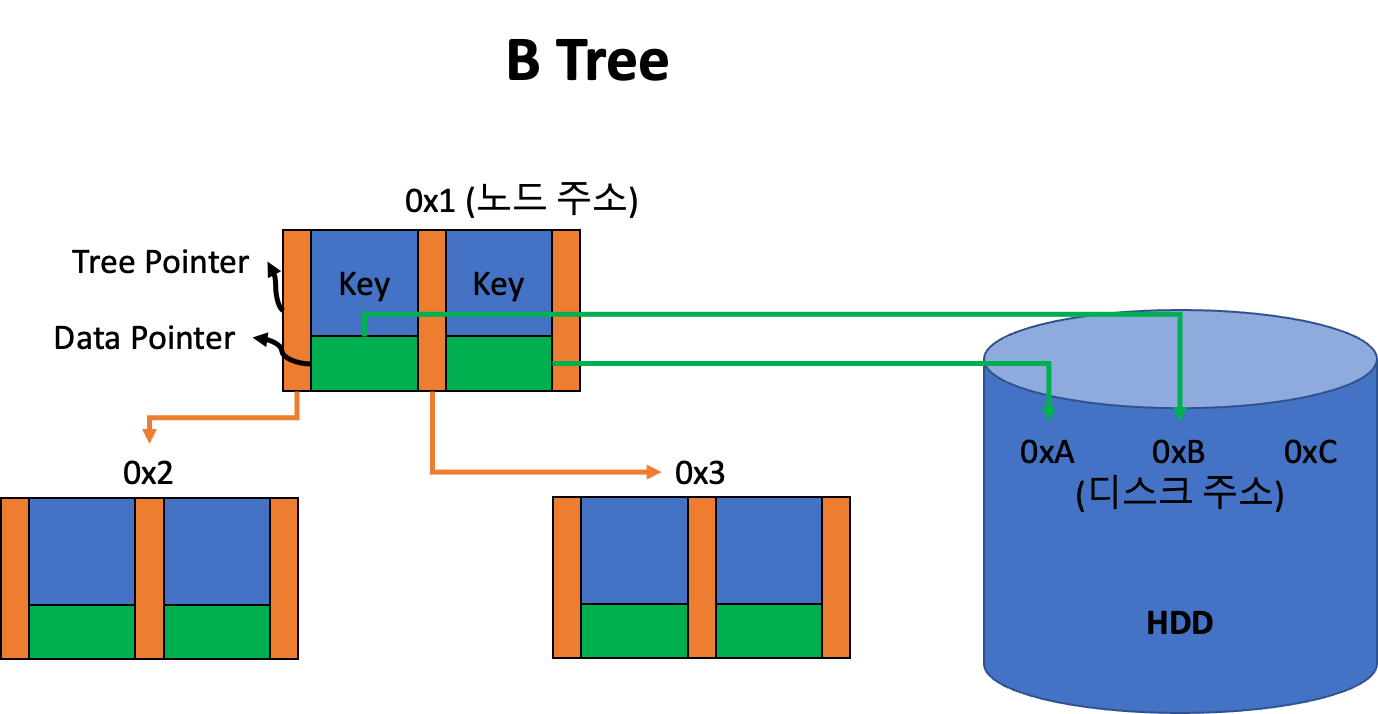
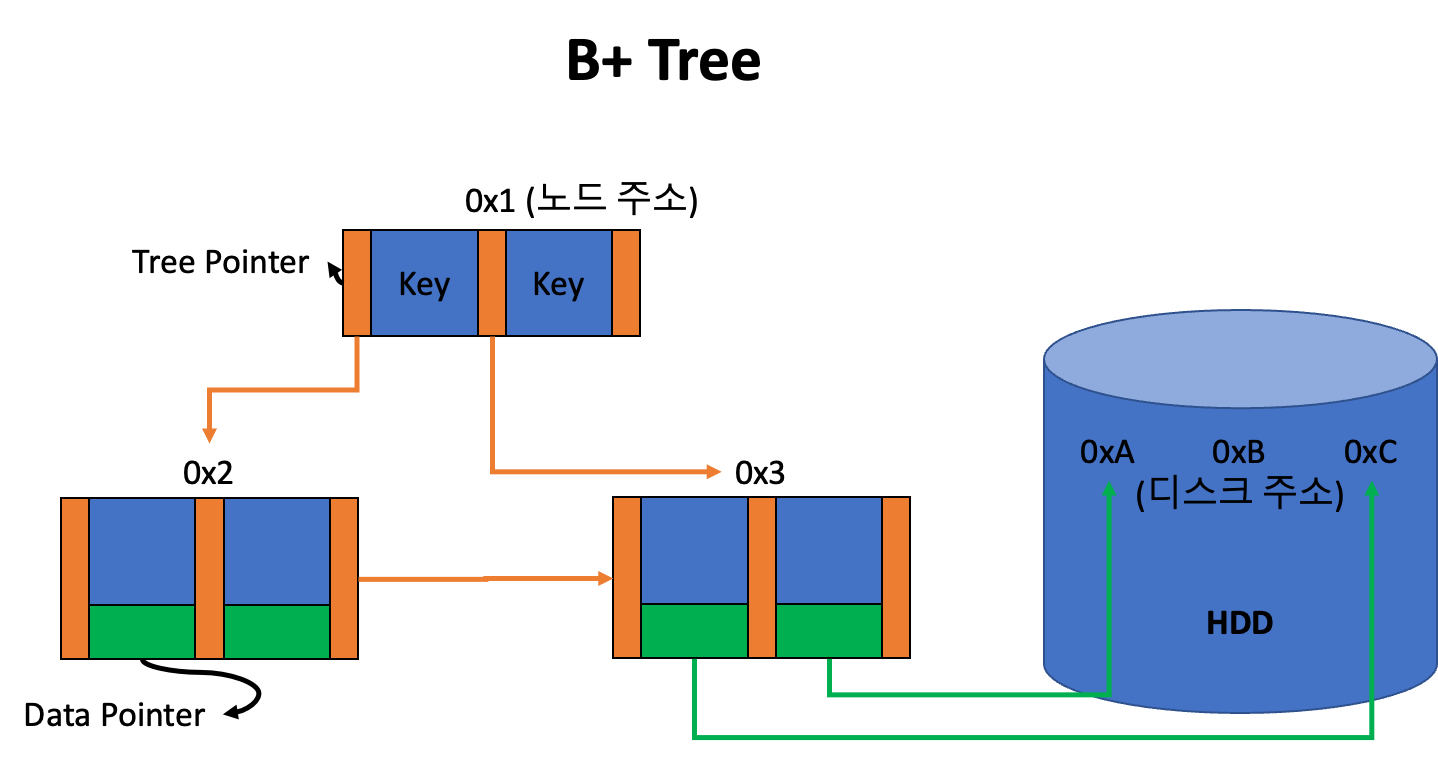
- B-Tree 는 모든 노드에
Key,Tree Pointer,Data Pointer가 존재한다. - B+Tree 의 인덱스 노드 (비단말노드) 에는
Key와Tree Pointer만 존재하고,Data Pointer는 존재하지 않는다. - B+Tree 의 데이터 노드 (리프노드) 에는
Key,Tree Pointer,Data Pointer가 모두 존재한다.
데이터 노드
- B Tree 에는 모든 노드가
Data Pointer를 가지고 있다. - B+ Tree 에는
Data Pointer가 리프노드에만 존재한다.- 따라서 삽입과 삭제 연산 모두 리프노드에서만 이루어진다.
