logo img Dev Blog

[CS Study] Stack & Queue

January 17, 2023

스택 & 큐

스택

Untitled

특징

  • 입력과 출력이 한 방향으로 제한된다.
  • LIFO (Last In First Out) 구조이다.

사용처

  • 함수의 콜스택
  • 문자열 역순 출력
  • 연산자 후위표기법

연산 종류

  • push : 데이터 삽입
  • pop : 최상위 데이터 추출
  • isEmpty : 비어있는지 확인
  • isFull : 꽉 차있는지 확인

스택 포인터 (SP)

  • push 와 pop 연산을 하려면 최상위 데이터의 위치를 알아야 한다.
  • 최상위 데이터의 위치를 스택 포인터 (SP)가 가지고 있다.
  • 초기값은 -1

Untitled

push 연산

public void push(Object o) {
	if (isFull()) return;
	
	stack[++sp] = o;
}
  • 스택이 꽉 차있다면 return
  • 아니면 스택의 최상위 요소 (sp) 위에 요소 삽입

pop 연산

public Object pop() {
	if (isEmpty()) return null;

	return stack[sp--];
}
  • 스택이 비어있다면 return null
  • 아니면 스택의 최상위 요소 (sp) return
    • 최상위 요소를 추출했으므로, sp는 1 감소

isEmpty 연산

private boolean isEmpty() {
	return sp == -1;
}
  • 스택이 비어있다면 sp는 -1

isFull 연산

private boolean isFull() {
	return sp == MAX_SIZE - 1;
}
  • 스택의 최대 크기만큼 요소가 채워져 있다면, sp 는 MAX_SIZE - 1

크기 제한이 없는 스택

  • 동적 배열을 활용하여, 크기 제한이 없는 스택을 구현할 수 있음
public void push(Object o) {
	if (isFull()) {
		Object[] newStack = new Obejct[MAX_SIZE * 2]; //크기가 2배인 새 스택 생성
		copyAry(stack, newStack); //기존 스택의 요소 복사
		stack = newStack; //새로 만든 스택으로 교체
		MAX_SIZE *= 2; //최대 크기를 2배로 증가
	}
	
	stack[++sp] = 0; //요소 추가
}

private void copyAry(Object[] fromAry, Object[] toAry) {
	for (int i = 0; i < fromAry.length; i++) {
		toAry[i] = fromAry[i];
	}
}


큐

Untitled

특징

  • 입력과 출력을 한 쪽 끝 (front, rear)으로 제한한다.
  • FIFO (First In First Out) 구조를 갖는다.

사용처

  • 버퍼 (Buffer)
    • 빠르게 입력된 작업들을 임시로 가지고 있는 공간
  • BFS

연산 종류

  • enqueue : 데이터 삽입
  • dequeue : 데이터 추출
  • isEmpty : 비어있는지 확인
  • isFull : 꽉 차있는지 확인

front, rear, size

  • front
    • 큐의 가장 첫 요소 (가장 먼저 들어온 요소)
    • dequeue 할 위치 기억
    • 초기값 = -1
  • rear
    • 큐의 가장 마지막 요소 (가장 늦게 들어온 요소)
    • enqueue 할 위치 기억
    • 초기값 = -1
  • size
    • 큐에 저장된 총 요소의 개수
    • 초기값 = 0

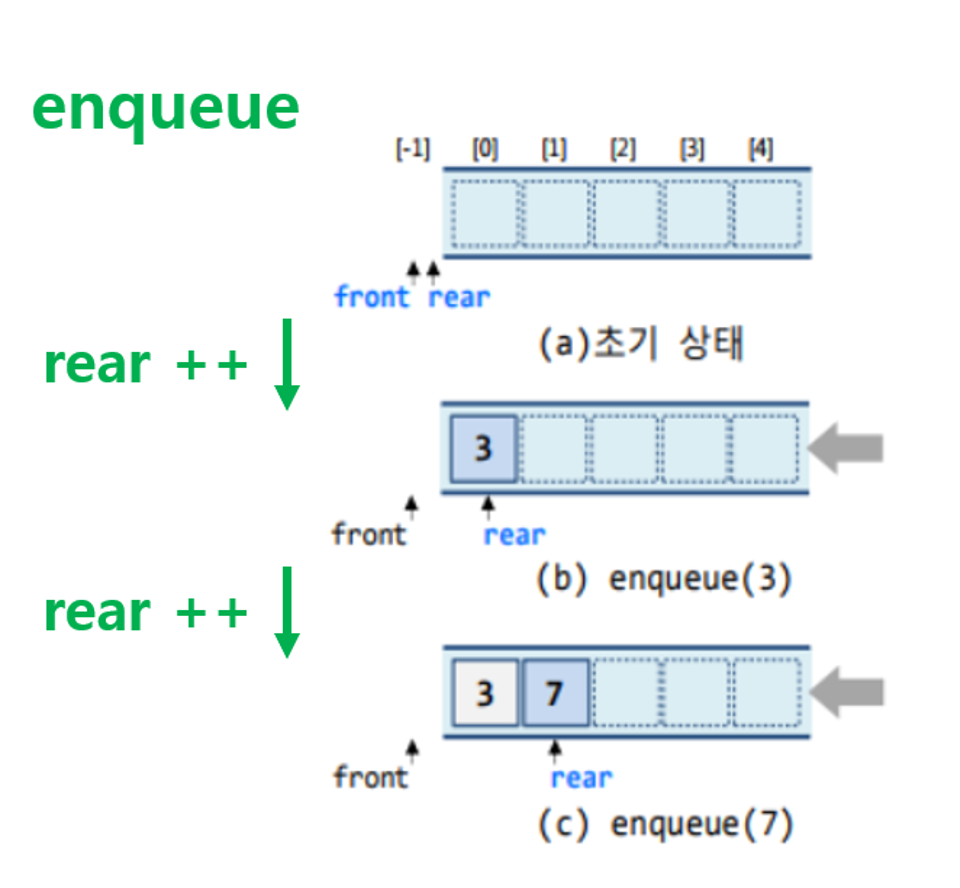
enqueue 연산

public void enqueue(Object o) {
	if (isFull()) return;

	queue[++rear] = o;
}
  • 큐가 꽉 차있다면 return
  • 아니면 rear를 1 증가시키고, 해당 위치에 요소 추가

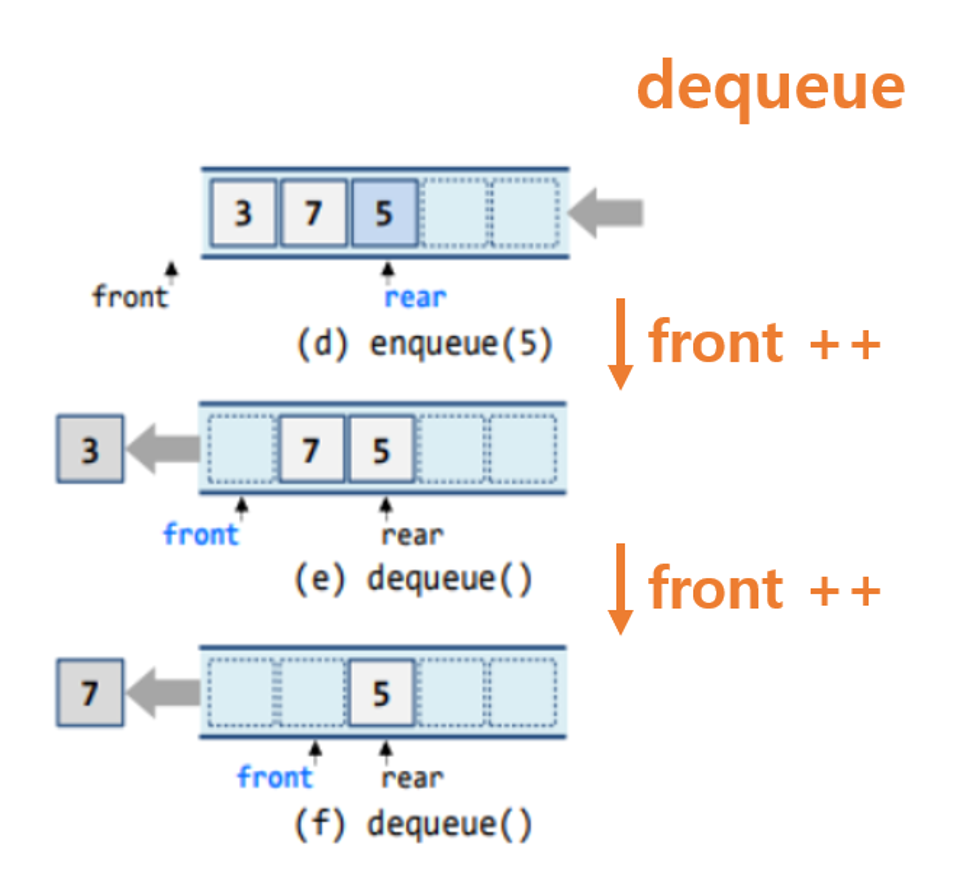
Untitled

dequeue 연산

public Object dequeue() {
	if (isEmpty()) return null;

	return queue[++front];
}
  • 큐가 비어있다면 return
  • 아니면 front를 1 증가시키고, 해당 위치의 요소 추출

Untitled

isEmpty 연산

private boolean isEmpty() {
	return front == rear;
}
  • front 와 rear 가 같다면 빈 상태로 판단

isFull 연산

//선형큐의 한계가 있는 코드
private boolean isFull() {
	return rear == MAX_SIZE - 1;
}

선형큐의 문제

  • enqueue 와 dequeue 연산을 반복하다보면 아래와 같은 상황이 발생한다.

      MAX_SIZE = 2 라고 가정
    
  [1. enqueue 연산]
  	front = -1
  	rear  = 0
  [2. enqueue 연산]
  	front = -1
  	rear  = 1
  [3. dequeue 연산]
  	front = 0
  	rear  = 1
  [4. dequeue 연산]
  	front = 1
  	rear  = 1
    
  결과적으로 rear == MAX_SIZE - 1 을 만족하게 됨
  • 2번 enqueue 하고 2번 dequeue 했다면, 큐가 비어있어야 정상이다.
  • 하지만 rear == MAX_SIZE - 1 을 만족하며, 큐가 가득 찬 상태로 판단하게 된다.

  • dequeue 를 할 때마다, 모든 요소들을 앞으로 이동시켜주면 문제를 해결할 수 있다.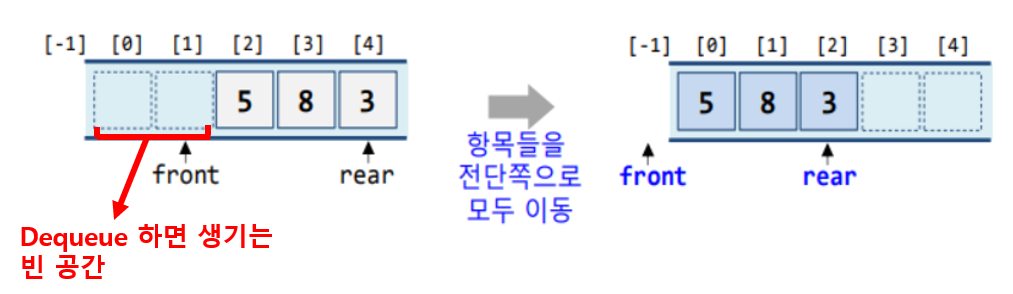

    Untitled

  • 하지만 이런 방식은 비효율적이다.
  • 원형큐를 통해 문제를 해결할 수 있다.

원형큐

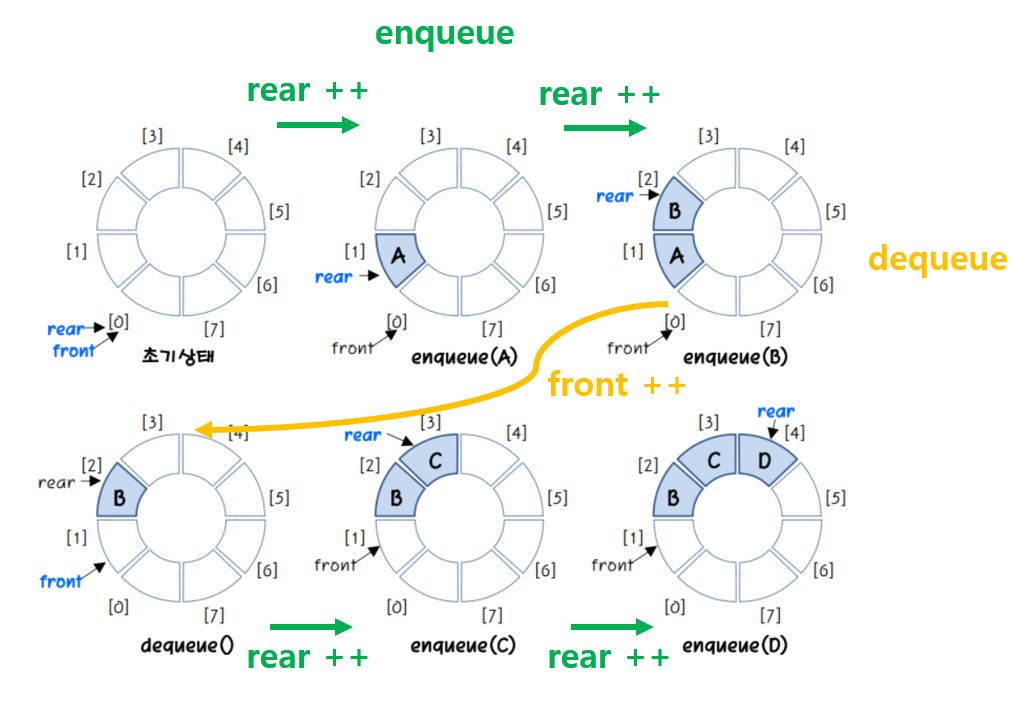
Untitled

  • 논리적으로 배열의 처음과 끝이 연결되어 있다고 간주한다.
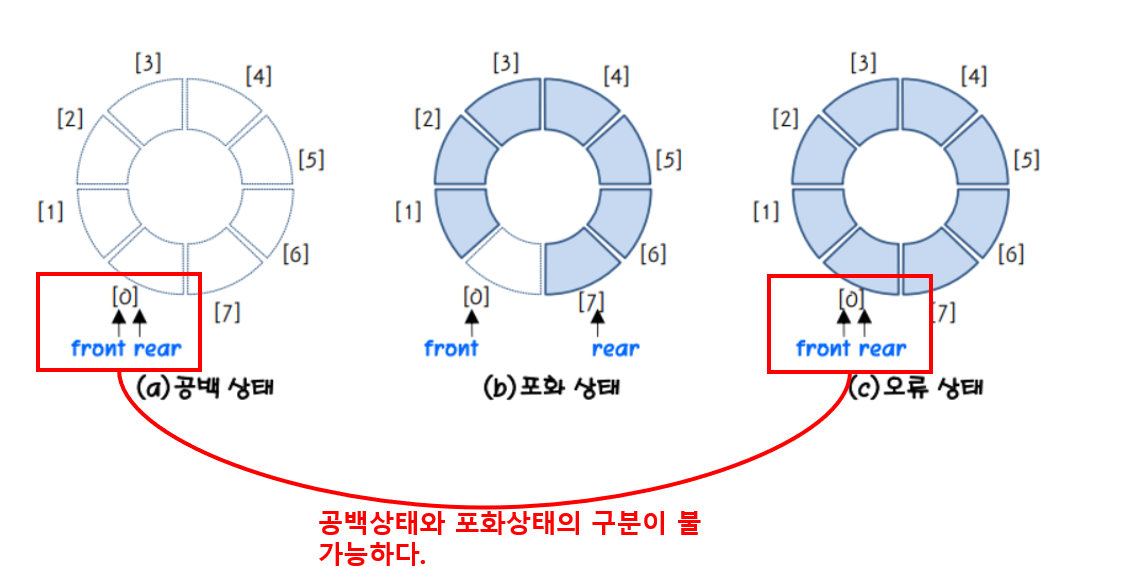
  • 초기 공백 상태인 경우, front와 rear가 0이다.
  • 공백, 포화 상태를 구분하기 위해, 항상 자리를 하나 비워둔다.

Untitled

원형큐 - enqueue 연산

public void enqueue(Object o) {
	if (isFull()) return;

	rear = (rear + 1) % MAX_SIZE;
	queue[rear] = o;
}
  • (rear + 1) % MAX_SIZE 을 통해, 순환할 수 있다.

원형큐 - dequeue 연산

public Object dequeue() {
	if (isEmpty()) return null;

	front = (front + 1) % size;
	return queue[front];
}
  • (front + 1) % MAX_SIZE 을 통해, 순환할 수 있다.

원형큐 - isEmpty 연산

private boolean isEmpty() {
	return front == rear;
}

원형큐 - isFull 연산

private boolean isFull() {
	return ((rear+1) % MAX_SIZE) == front;
}