분할 정복 : 최근접 점의 쌍 찾기

개요

최근접 점의 쌍 문제란?

2차원 평면상의 n개의 점이 입력으로 주어질 때, 거리가 가장 가까운 한 쌍의 점을 찾는 문제

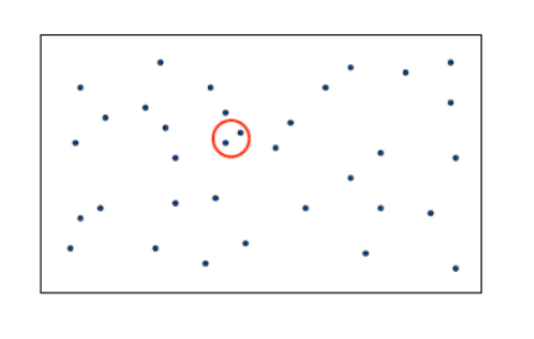
최근접 점의 쌍 문제

기본 해결 방식

모든 점에 대하여 각각의 두 점 사이의 거리를 계산하여 가장 가까운 점의 쌍 찾는다.
⇒ $O(n^2)$
n개의 점을 각각 (n-1)번씩 비교한다.

보다 나은 해결 방식

n개의 점을 1/2로 분할한다.
각 부분해 중 최근접 점 쌍을 찾는다.
분할한 영역 사이의 중간영역에서 최근접 점 쌍을 찾는다.
찾은 3개의 쌍 중 가장 작은 쌍 반환한다.

해결방식

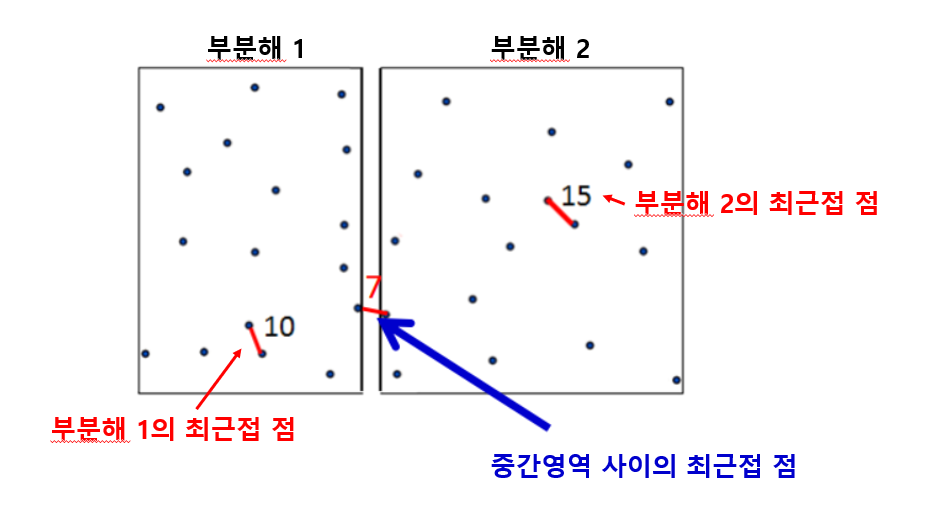
고려사항

반드시 중간 영역의 최근접 점까지 찾아야함

중간 영역

범위 설정

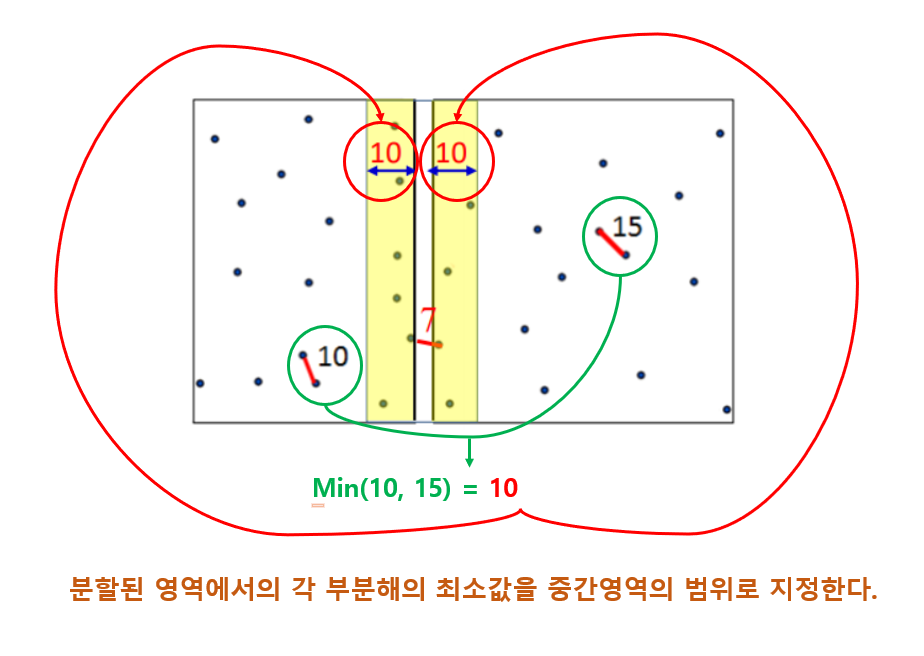
중간 영역의 범위 = d
d = min{“왼쪽 부분의 최근접 점의 쌍 거리”, “오른쪽 부분의 최근접 점의 쌍 거리”}

속한 점 찾는 방법

x좌표 기준 정렬 후, 분할기준을 찾는다.
중간 영역에 속한 점
- ‘왼쪽 부분 문제의 가장 오른쪽 점의 x좌표’ - d
- ‘오른쪽 부분 문제의 가장 왼쪽 점의 x좌표’ + d
- 중간 영역에 속한 점 = 위 두 x값 사이의 “x값을 가진 점들”

예시
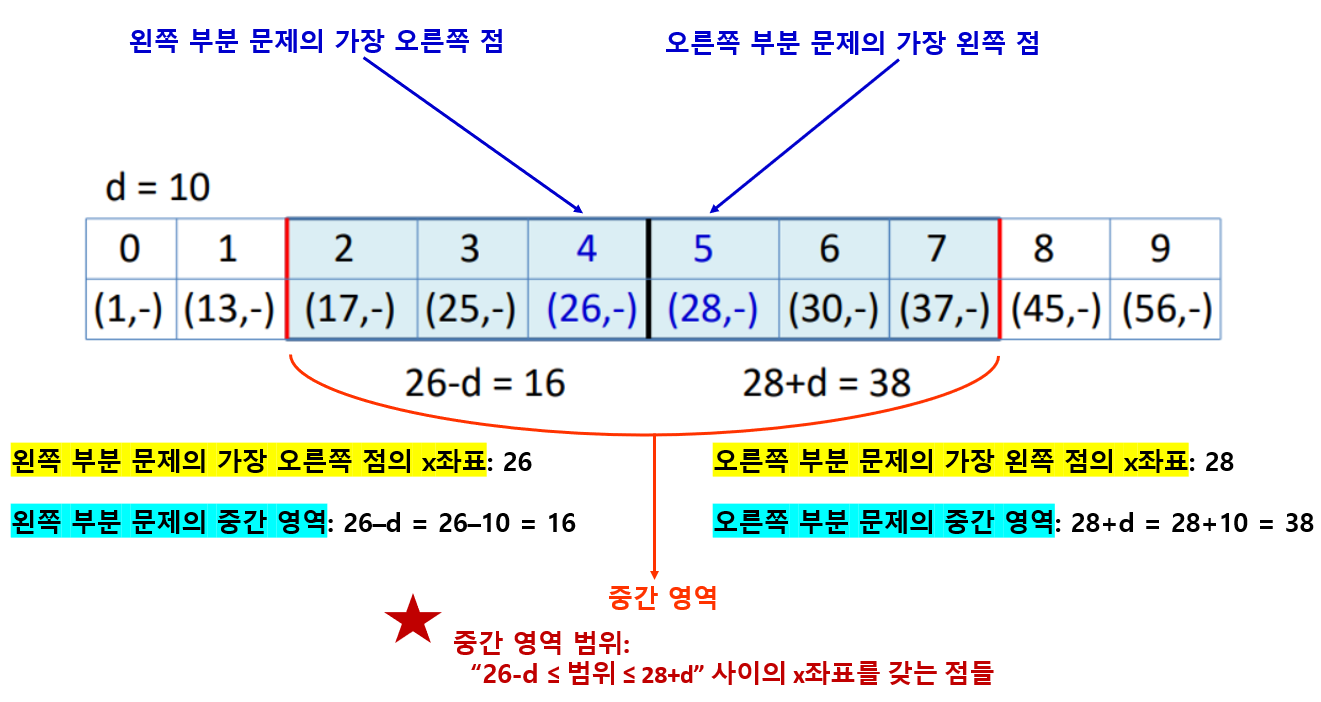
- d=10 일 때
즉, 16 ~ 38 사이의 값을 x좌표로 가지는 점 == 중간 영역의 점

속한 점 비교 방법

한 쪽의 각 점마다 반대편의 각 점을 비교한다.

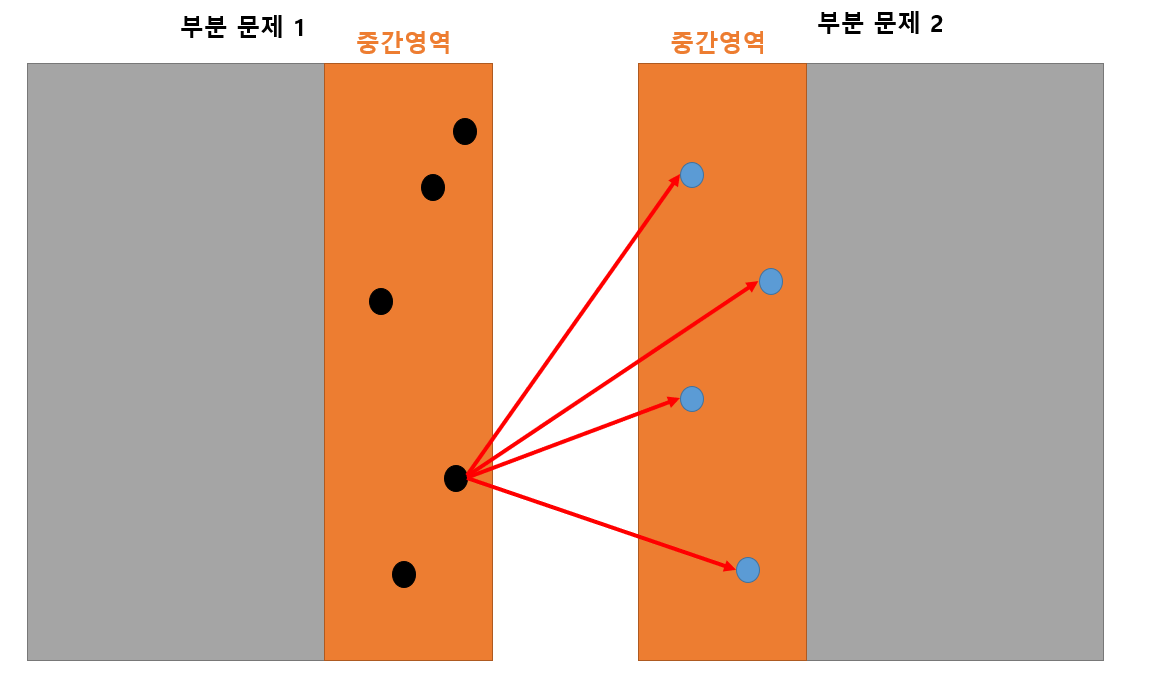
속한 점 비교 방법

하지만 중간영역의 범위(주황색 영역)를 넘지 않는 범위 안에서만 비교한다.

아래에서 자세히 설명한다.

알고리즘

의사코드

절차 : 1번 라인

점의 개수가 3 이하라면 아래 항목 수행
- “점의 개수 == 3”인 경우
  - 3개의 점들 사이의 최근접 쌍 반환
- “점의 개수 == 2”인 경우
  - 2개의 점 쌍 반환

절차 : 2번 라인

문제를 부분 문제로 분할하는 라인

절차 : 3, 4번 라인

재귀호출을 통해 왼쪽, 오른쪽의 최근접 점의 쌍을 구한다.

절차 : 5번 라인

반환된 “왼쪽, 오른쪽 최근접 점의 거리” 중 작은 값을 d로 설정한다.
중간 영역에 속하는 점들 중 최근접 점의 쌍을 구한다.

절차 : 6번 라인

정답 반환

시간 복잡도

배경 전재

입력 s에 총 n개의 점이 존재한다고 가정한다.

전처리 과정 : 정렬

s의 점들을 x좌표의 오름차순으로 정렬
참고로, 퀵 정렬의 시간복잡도는 $O(nlogn)$ 이다.
∴ $O(nlogn)$

line : 1

3개 이하의 점들의 최근접 점 구하기
- 점의 개수가 2개인 경우
  - 거리 계산 총 1번 ⇒ $O(1)$
- 점의 개수가 3 개인 경우
  - 거리 계산 총 3번 ⇒ $O(1)$
    
    계산을 1번하나, 3번하나 차이가 없다.
∴ line1의 시간복잡도 = $O(1)$

line : 2

동일한 크기로 분할하기
- 정렬된 s를 분할할 때
  - 이미 정렬이 되어있으므로, s의 중간 인덱스로 분할하면 됨
    ⇒ $O(1)$

∴ line2의 시간복잡도 = $O(1)$

line : 3, 4

재귀적 호출을 수행한다.
호출과정
- 합병정렬과 동일한 과정
∴ 고려X (호출자체는 시간소요X)
단, 가장 마지막 부분해의 계산이 끝난 후,
합병할때의 시간복잡도 = 층수*입력개수 = ![O(log_2n)n=O(nlog_2n)=O(nlogn)](https://latex.codecogs.com/svg.image?O(log_2n)n=O(nlog_2n)=O(nlogn))

line : 5

중간영역의 범위를 구한다.
중간영역의 최근접 점을 찾는다.

중간영역의 최근접 점 찾는 과정
1. 중간영역에 있는 점들을 y좌표의 오름차순으로 정렬한다.
2. “아래에서 위” or “위에서 아래”로 각 점들을 기준으로 거리를 비교한다.
  
  이때, 각 점을 기준으로 거리가 d 이내인 주변의 점들 사이의 거리만 계산

시간복잡도
- y좌표 오름차순 정렬
  ⇒ $O(nlogn)$
- 각 점들의 거리 비교
  - 주변 점들의 거리 계산시, d보다 먼 거리의 점들은 고려할 필요가 없다.
  - d보다 먼 거리에 있는 점들은 어차피 “왼쪽, 오른쪽 부분해를 구할 때” 계산되어 제외되기 때문이다. (즉, 결과에 영향을 미치지 않음)
  - 따라서, 비교할 점들의 개수는 d로 인해 제한된다.
    ⇒ $O(1)$
  - 그러므로 각 점들간의 거리를 비교할 때의 시간복잡도는 $O(1)$ 이다.
∴ line5의 시간복잡도 = $O(nlogn)+O(1)$

line : 6

$min(CP_L,CP_R,CP_C)$ 을 수행한다.
3개 중 가장 작은 값을 구하는 시간복잡도
⇒ $O(1)$

∴ line6의 시간복잡도 = $O(1)$

합병

층수 구하기

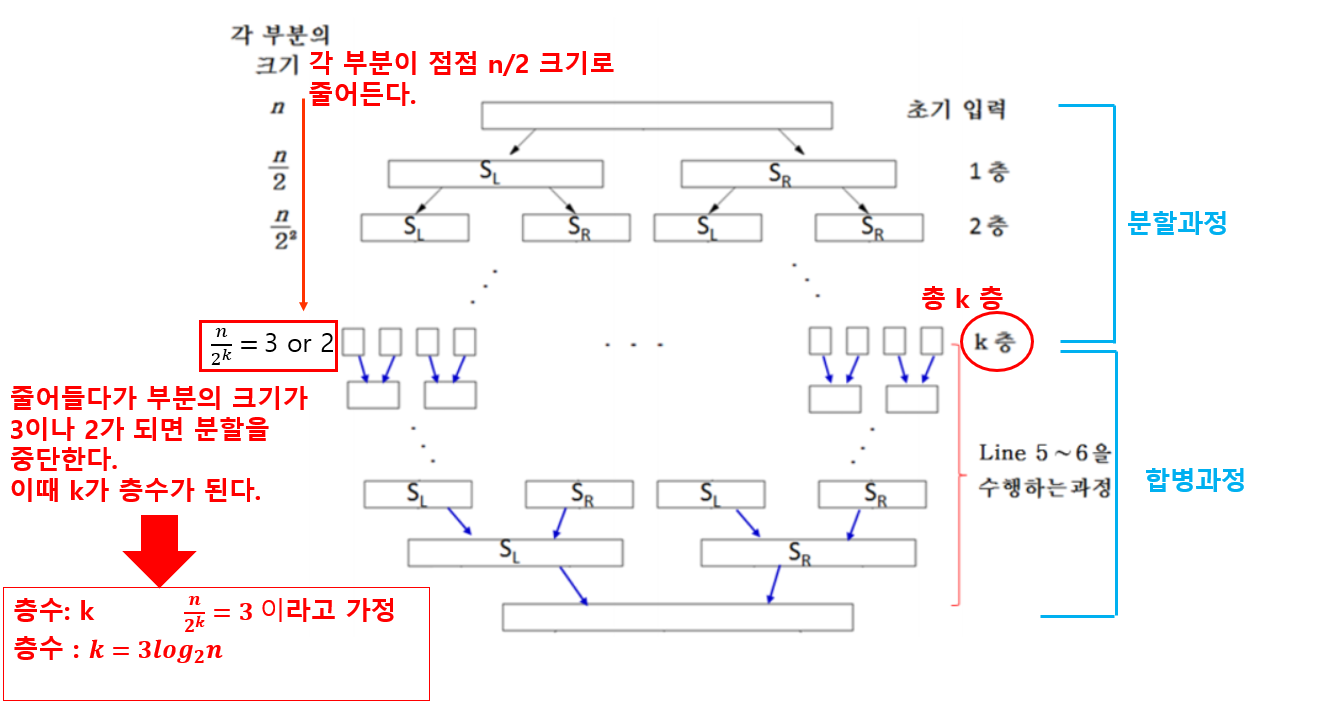
각 층 계산 시간복잡도

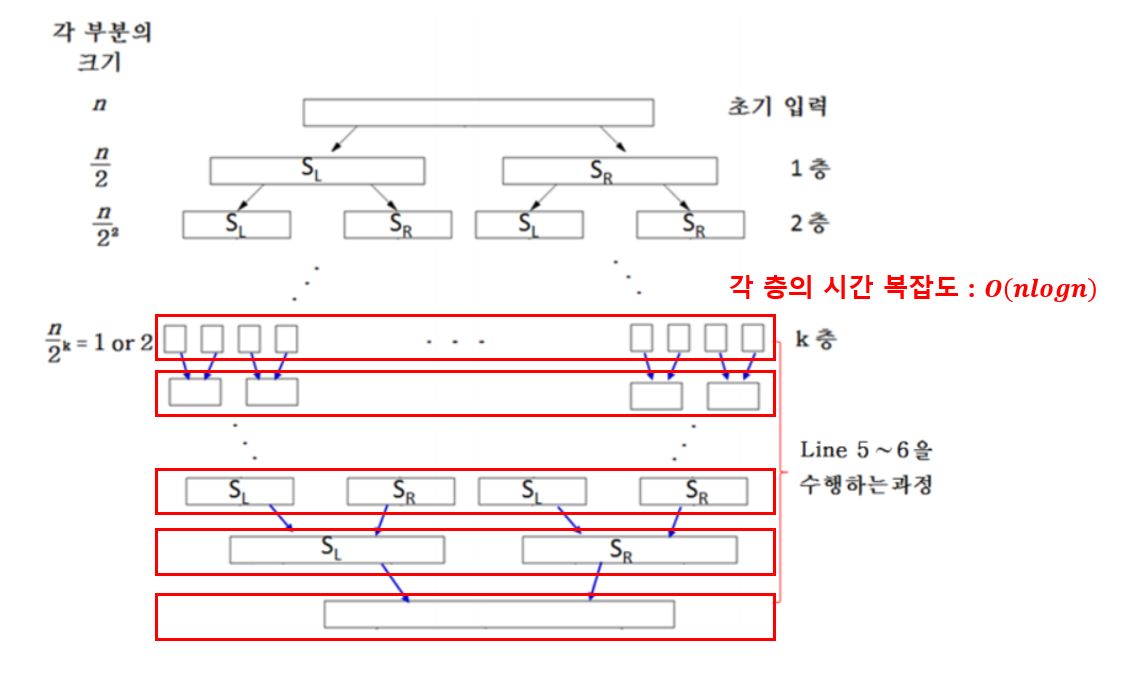
line1복잡도 + line2복잡도 + line3복잡도 + line4복잡도 + line5복잡도 + line6복잡도 =
$O(1)+O(1)+none+none+[O(nlogn)+O(1)]+O(1)=O(nlogn)$

따라서,
(각층_시간복잡도) * (층수) = (최근접 점 알고리즘 시간복잡도)

시간복잡도 결론

(각층_시간복잡도) * (층수) = (최근접 점 알고리즘 시간복잡도) =
$O(nlogn)*3log_2n=O(nlogn)*O(logn)=O(nlog^2n)$

중간영역 점들의 거리 계산 시간복잡도 증명

중간영역을 ‘변의 크기가 d/2인 정사각형’으로 쪼갠다.
각 정사각형에는 점이 하나씩만 들어있다.
- <증명>
  - 가정: 정사각형마다 점이 2개있다.
  1. 정사각형 내부의 점들의 최대 거리: $\sqrt{(d/2)^2+(d/2)^2}=d/\sqrt{2}$
  2. 이때, $d/\sqrt{2}<d$ 이다.
  3. 그렇다면 $CP_L$ 과 $CP_R$ 을 계산할 때, 최솟값으로 도출이 되었어야 한다.
  4. 하지만, $min(CP_L,CP_R)=d$ 이므로, 모순이다.
  5. 따라서, 각 정사각형에는 점이 하나씩만 들어있다.
각 정사각형에는 점이 하나씩만 들어있으므로, 하나의 점에서 3개의 행 이상 차이나는 점들에 대해서는 무시해도 된다.
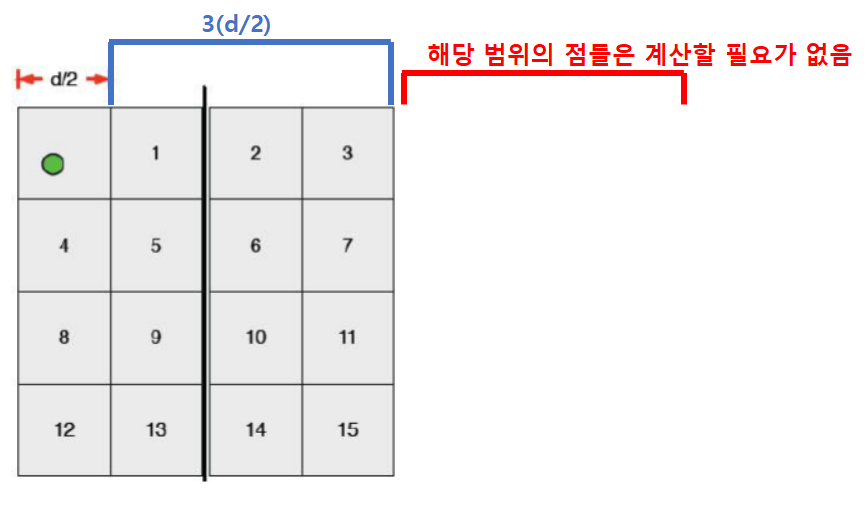
따라서, 중간영역의 시간복잡도는 $O(1)$ 이다.

성결대학교 컴퓨터 공학과 임태수 교수님 (2021)
양성봉, 『알기 쉬운 알고리즘』

본 게시글은 위 강의 및 교재를 기반으로 정리한 글입니다.