분할 정복 : 선택문제 (Selection)
개요
선택 문제란?
- n개의 숫자들 중에서 k번째로 작은 숫자를 찾는 문제
기본 해결 방식
-
최소 숫자를 k번 찾는다. 단, 각 최소 숫자를 찾은 뒤에는 입력에서 최소 숫자 제거.
⇒k:
k번째로 작은 수 (몇 번째로 작은 수를 찾느냐에 따라 복잡도 변화) -
숫자들을 정렬한 후, k번째 숫자를 찾는다.
⇒
보다 나은 해결 방식
- 이진 탐색 활용하여 해결할 경우 효율적이다.
이진 트리가 아니다!
특징 - 이진 탐색 활용시
- 분할 정복 알고리즘이기도 하지만 랜덤 알고리즘이기도 하다.
왜냐하면 피봇이 무작위로 설정되기 때문이다.
- 피봇이 입력 리스트를 너무 한쪽으로 치우치게 분할 시
⇒ 알고리즘의 수행 시간 길어짐 - 입력이 치우치게 분할될 확률 = 1/2
선택 문제 해결
원리 : 이진 탐색 이용
- 입력을 1/2로 나눈 두 부분 중에서 한 부분만을 검색
- 피봇을 선택하여 분할
- 피봇을 기준으로 SmallGroup, LargeGroup 분류
- 분류된 그룹 중 “적합한 그룹 한 개”에서만 탐색하면 된다.
원리 : 탐색할 그룹 선택하기
- k번째로 작은 수를 찾을 때, k번째 작은 숫자가 속한 그룹을 판단해야한다.
예시
-
찾는 값이 SmallGroup에 있을 경우
- 입력된 숫자의 개수 : n = 7
- 2번째로 작은 숫자 찾기
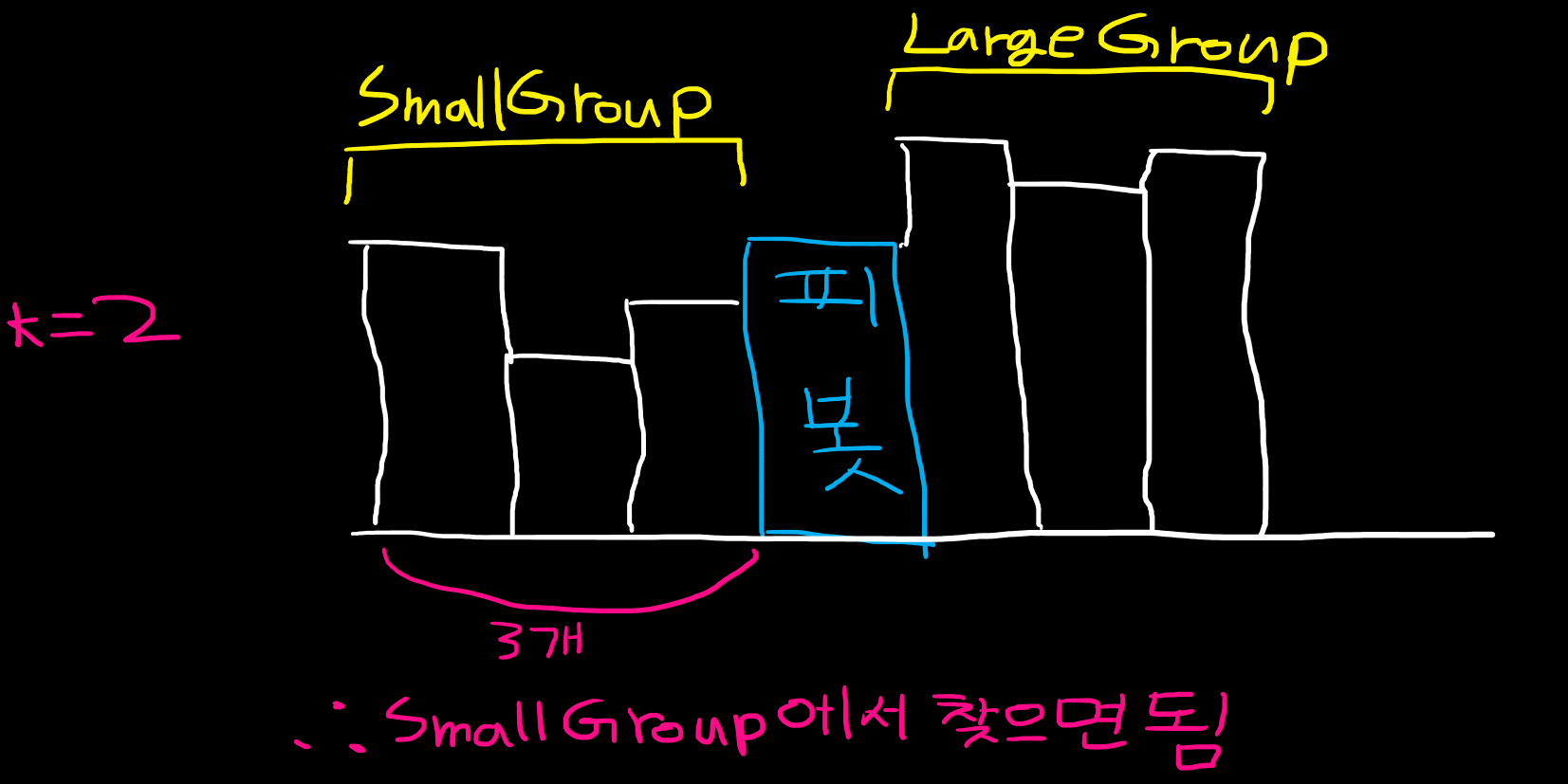
-
찾는 값이 LargeGroup에 있을 경우
- 입력된 숫자의 개수 : n = 7
- 5번째로 작은 숫자 찾기
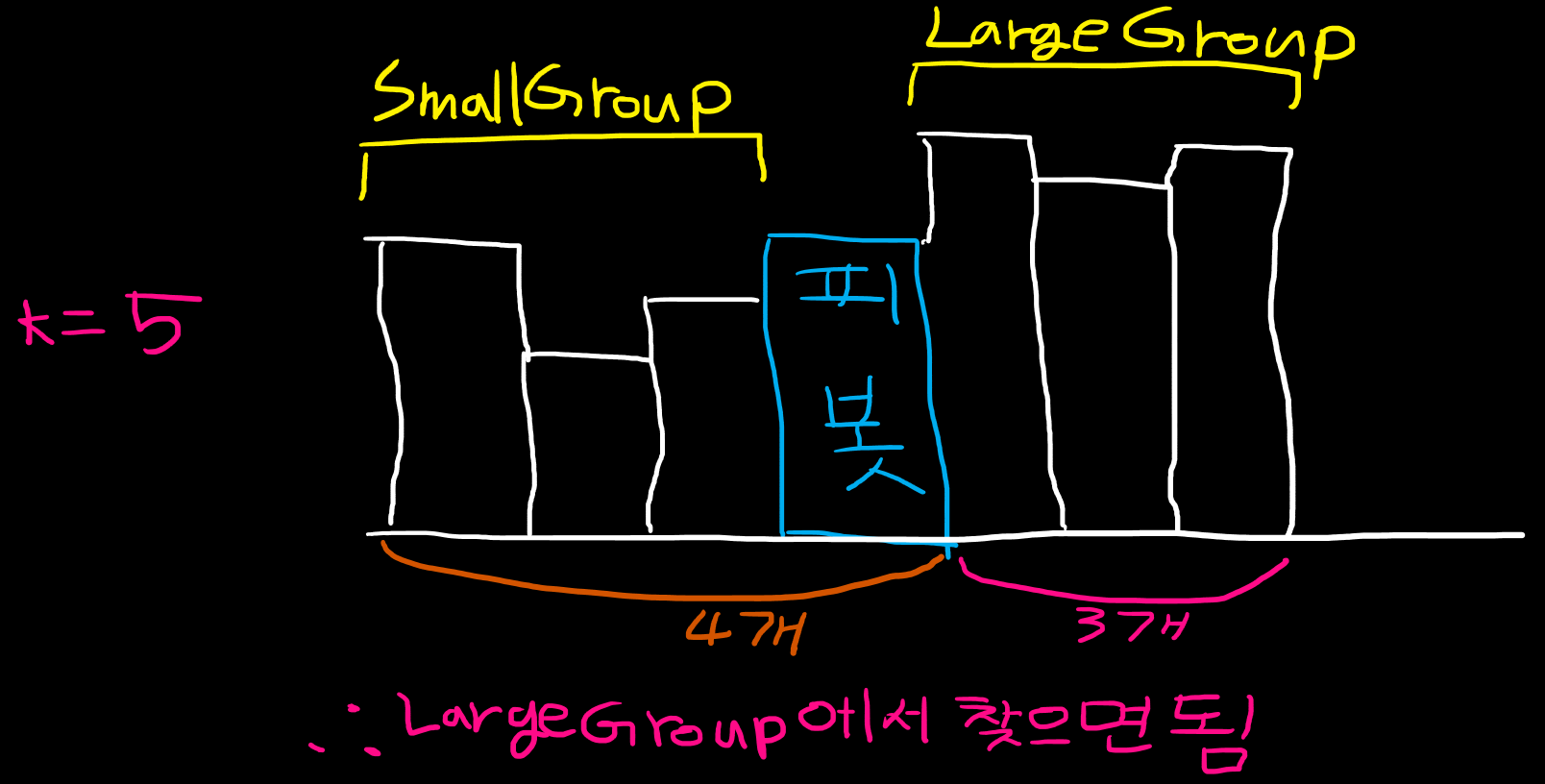
- 정리
- Small Group에 k 번째 작은 숫자가 속한 경우
- k번째 작은 숫자를 Small Group에서 탐색
- Large Group에 k 번째 작은 숫자가 속한 경우
-
(k - SmallGroup’s_Size - 1) 번째로 작은 숫자를 Large Group에서 탐색
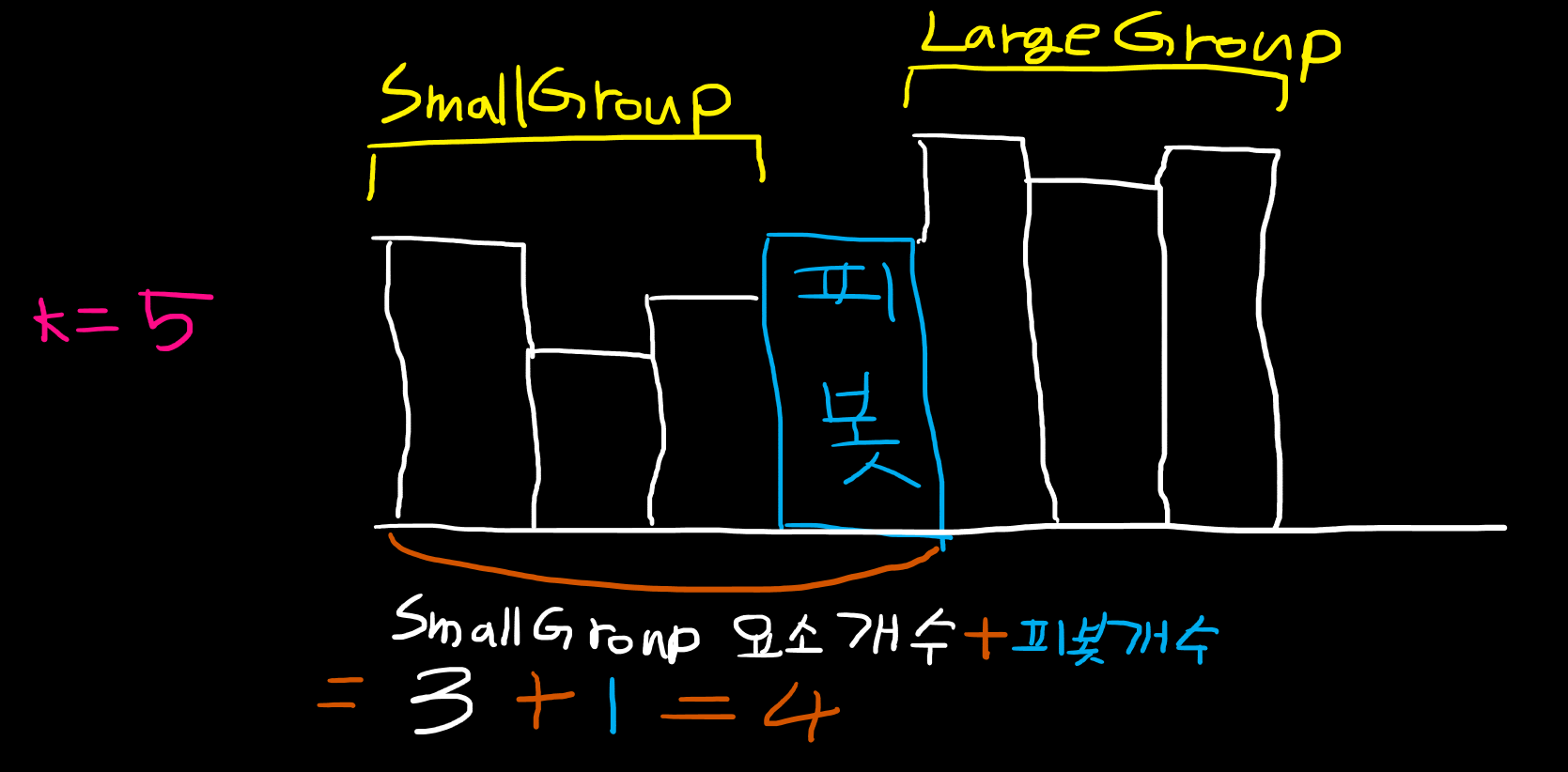
-
- Small Group에 k 번째 작은 숫자가 속한 경우
알고리즘
의사코드

절차 : 1~4번 라인
- 퀵 정렬 수행 (only 그룹 분할까지만)
절차 : 5번 라인
- Small Group의 크기 (요소개수) 계산
-
Small Group의 크기 = (p - 1) - left + 1
- 변수 설명 (변수 p)
- 피봇이 아직 A[left]에 위치할 때
- p=SmallGroup의 가장 오른쪽 요소의 인덱스값
- 피봇이 A[p]로 이동했을 때
- p=피봇의 인덱스값
- 피봇이 아직 A[left]에 위치할 때
절차 : 6번 라인
- k번째 작은 수가 SmallGroup에 존재한다면, Selection(A, left, p-1, k) 호출
- 변수 설명
- A
- A는 배열
- left, p-1
- SmallGroup 내에서 찾으므로 SmallGroup의 “첫 요소인덱스”~”마지막 요소인덱스”로 호출
- k
- SmalllGroup 내에서 k번째로 작은 수
- A
절차 : 7번 라인
- k번째 작은 수가 피봇일 경우 피봇을 반환한다.
절차 : 8번 라인
-
k번째 작은 수가 LargeGroup에 존재한다면, Selection(A, p+1, right, k-S-1) 호출한다.
-
변수 설명
- A
- A는 배열
- p+1, right
- SmallGroup 내에서 찾으므로 LargeGroup의 “첫 요소인덱스”~”마지막 요소인덱스”로 호출
- k-S-1
- Large Group에서 k-S-1번째로 작은 수
- Large Group에서 찾아야하는 수의 index번호 :
k - (SmallGroup크기 + 피봇크기)
- A
반복
- 정답을 도출할 때까지 반복
good 분할과 bad 분할
bad 분할
- 분할될 두 그룹 중의 하나의 크기가 입력 크기의 3/4과 같거나 크게 분할될 때
good 분할
- bad분할의 반대

bad, good 분할의 확률 : 각각 1/2
good 분할, bad 분할의 확률

시간 복잡도
피봇 선택 조건
- 2번씩 선택해야한다.
-
왜냐하면 “good분할이 될 확률 == 1/2” 이므로,
피봇 2번 선택시 평균적으로 good 분할이 적용된다. -
그러므로 계속해서 good분할일 경우의 시간복잡도를 구한뒤, 2를 곱하면 된다.
-
good분할만 있을 때의 시간 복잡도
- 리스트 크기가 3/4배로 연속적으로 감소
selection알고리즘의 총 시간 복잡도
- O(n) * 피봇2번선택 = 2=O(n))
selection알고리즘 - 응용법
활용법
-
중앙값(median) 찾는데 활용 가능
평균값 단점:
한 개라도 매우 큰 숫자라면 왜곡됨
- 성결대학교 컴퓨터 공학과 임태수 교수님 (2021)
- 양성봉, 『알기 쉬운 알고리즘』
