BFS : 개념
개요
BFS란?
- Breadth First Search의 약자로, 너비 우선 탐색 알고리즘이다.
- 그래프 구조에서 탐색을 위해 사용되는 탐색 알고리즘이다.
- 그래프의 모든 노드들을 방문(탐색)해야 한다.
- 가까운 노드부터 탐색하는 알고리즘이다.
- 큐(Queue) 자료구조를 이용하는 것이 정석이다.
- 인접한 노드를 반복적으로 큐에 넣도록 알고리즘을 작성하면 자연스럽게 먼저 들어온 것이 먼저 나가게 되어, 가까운 노드부터 탐색을 진행하게 된다.
BFS 동작 과정
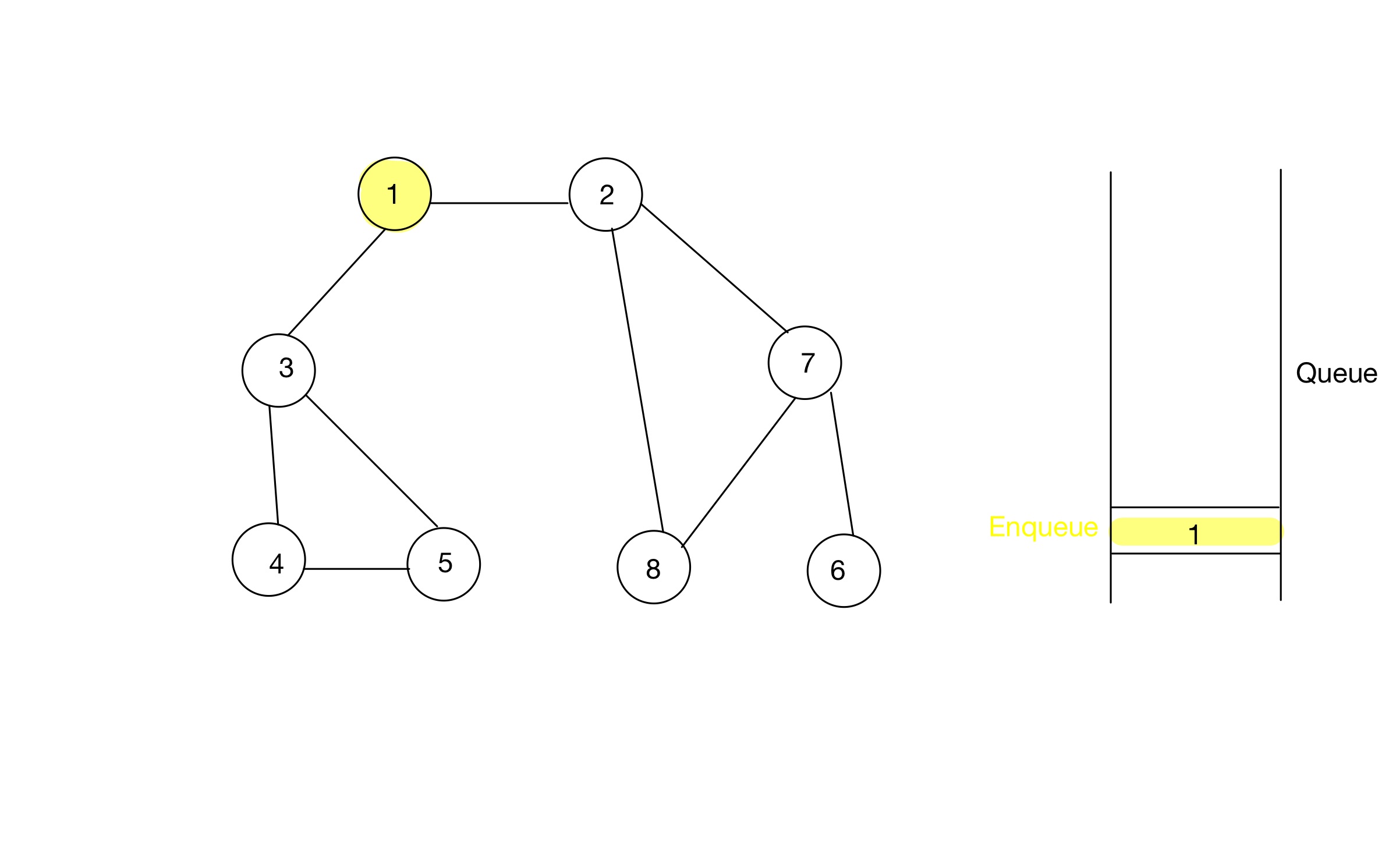
- 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
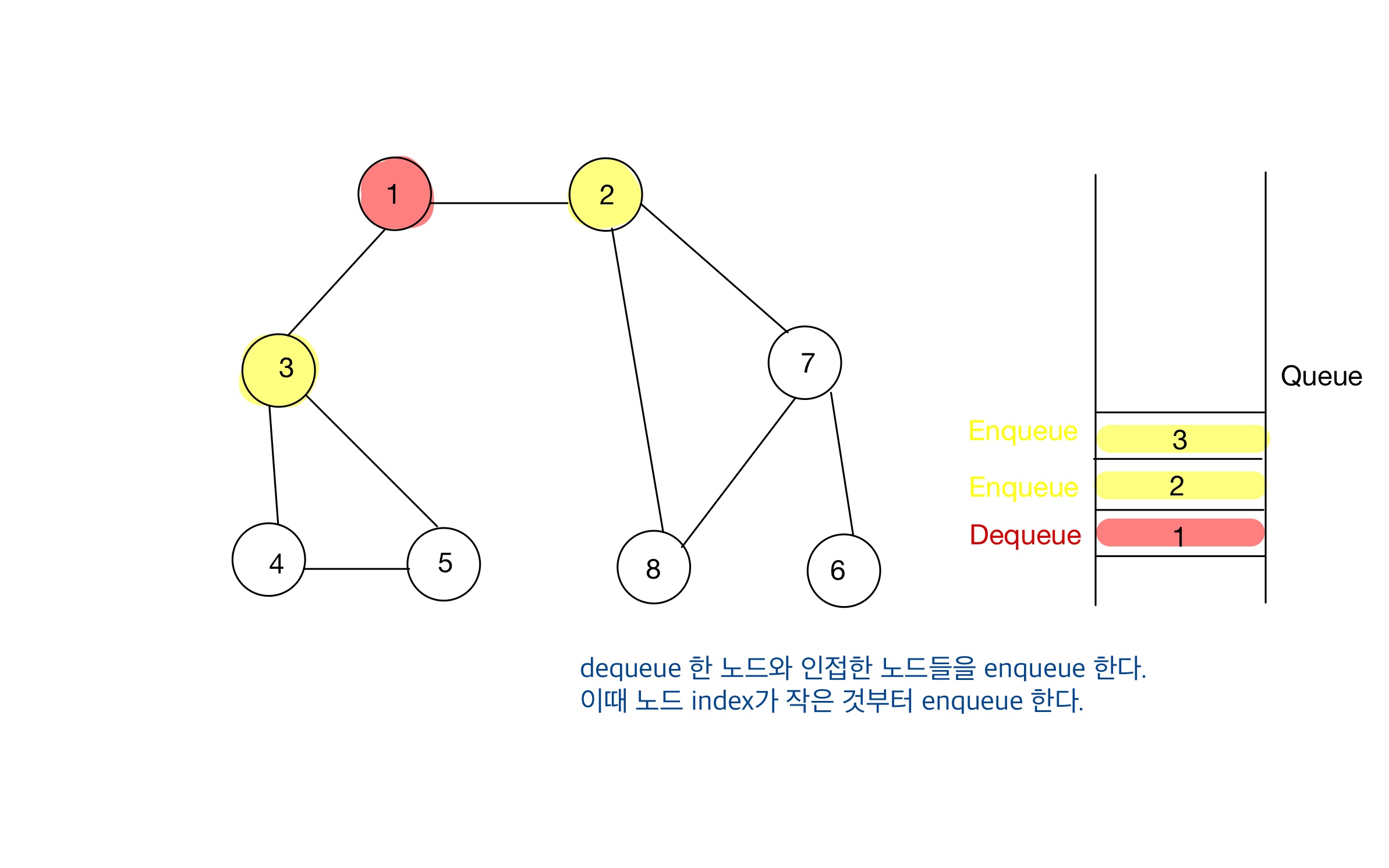
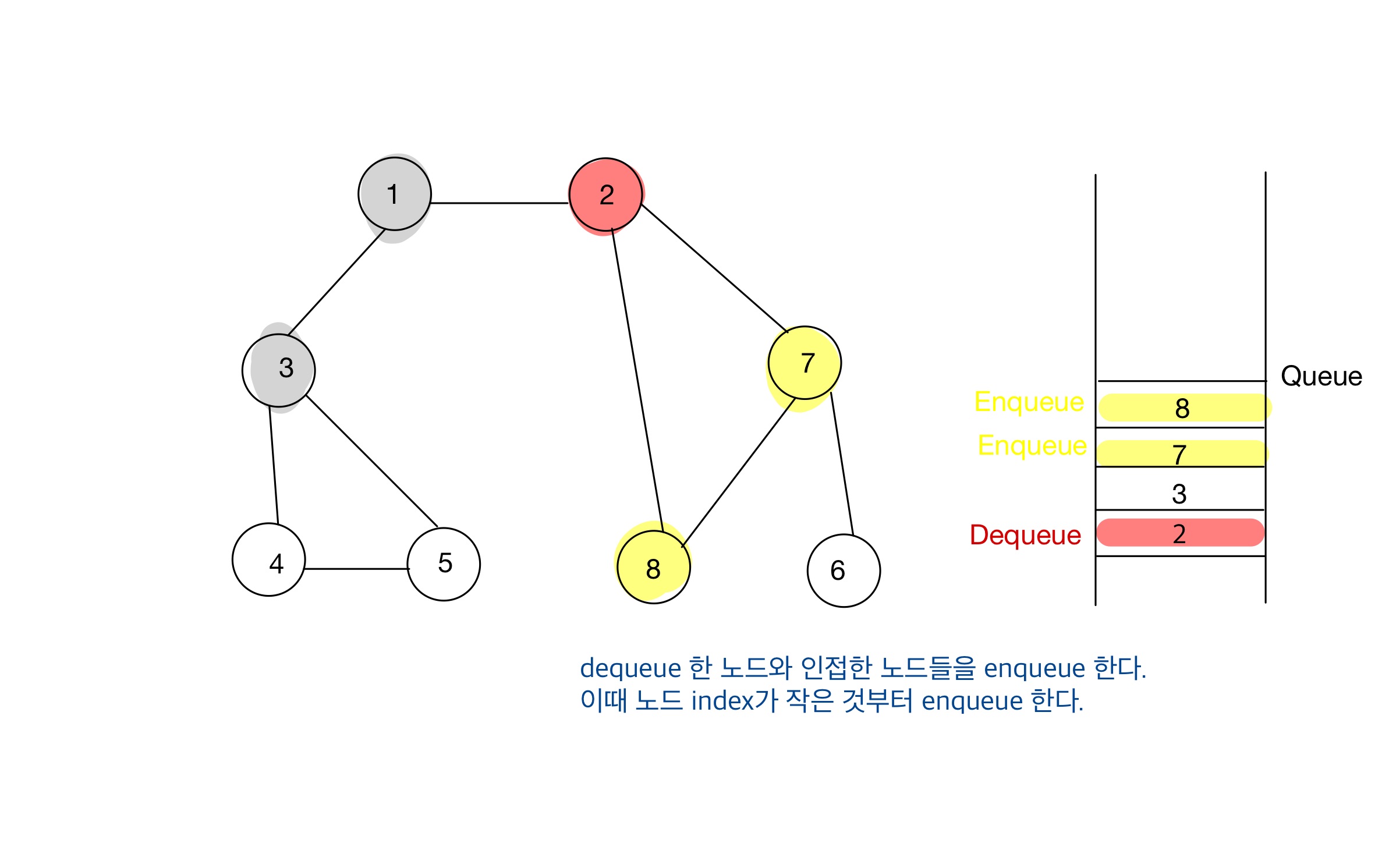
- 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리를 한다.
- 2번 과정을 더 이상 수행할 수 없을 때까지 반복한다.
BFS에서 인접 노드를 선택(enqueue)할 땐, 가장 낮은 번호를 갖는 노드부터 선택하는 것이 좋다.
예시
예시에서 사용할 그래프 형태
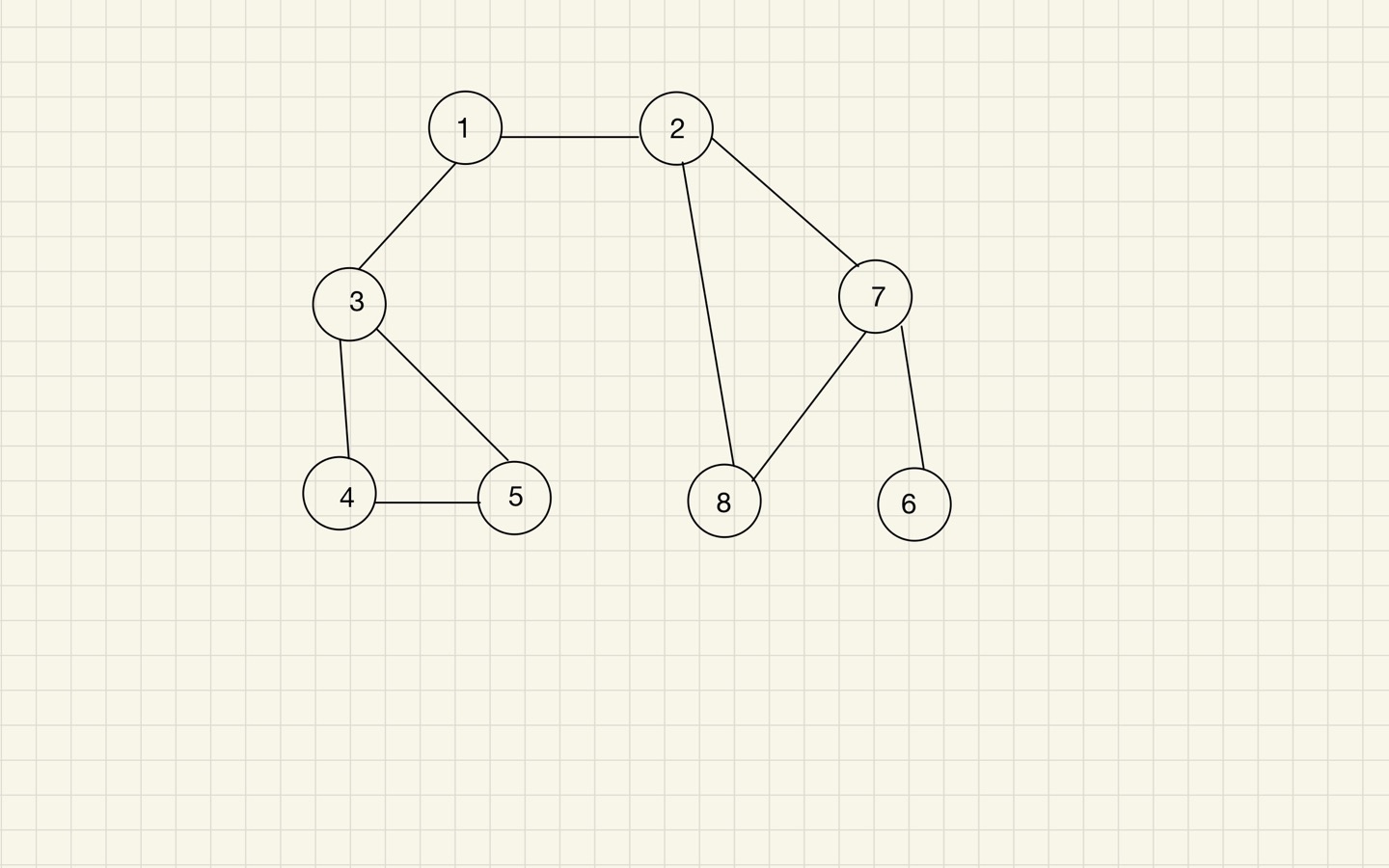
8번 노드가 1번 노드가 아닌 2번 노드와 인접함에 주의하자!
(교재와 다르다.)
Step 01
Step 02
Step 03
Step 04
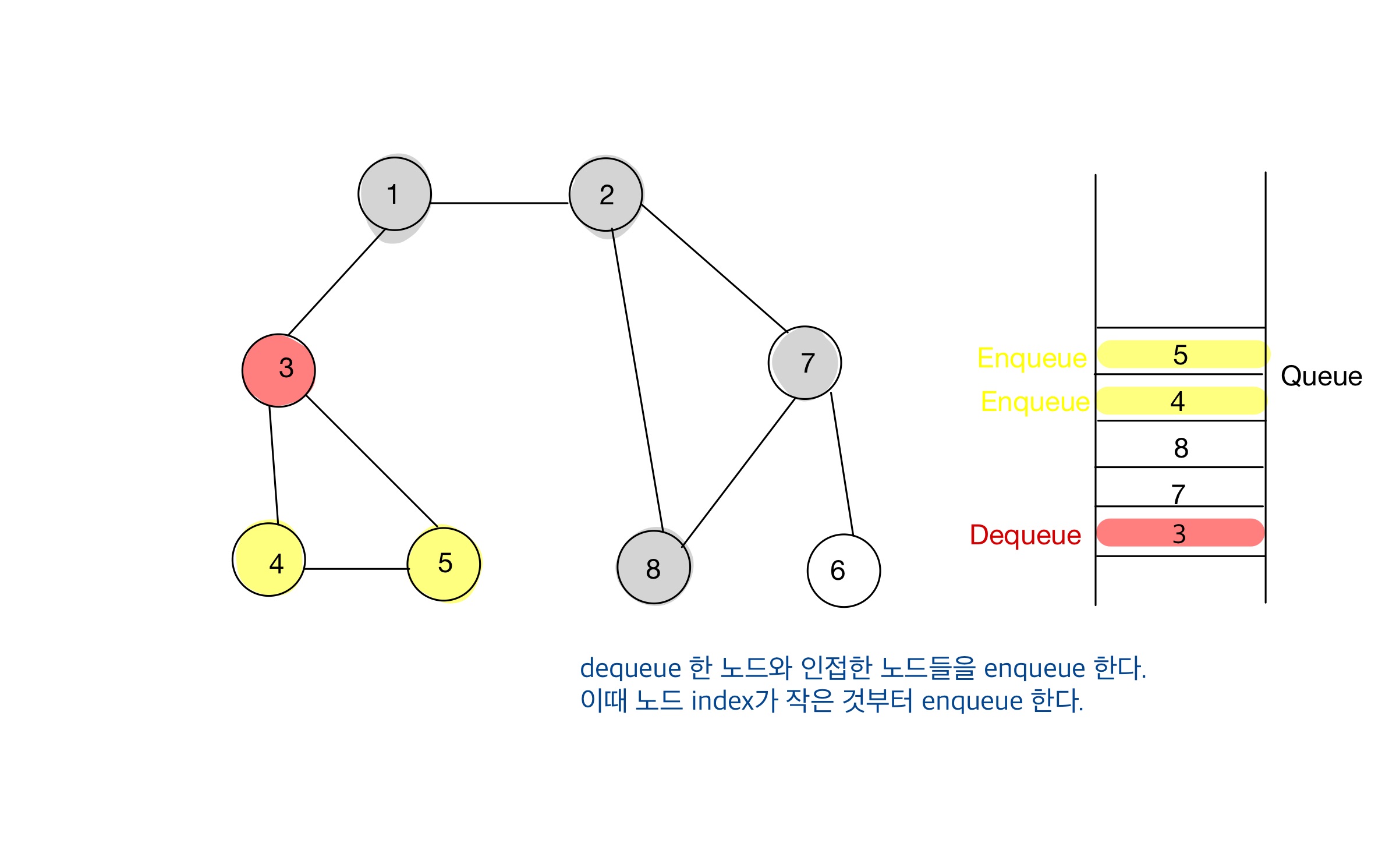
Step 05
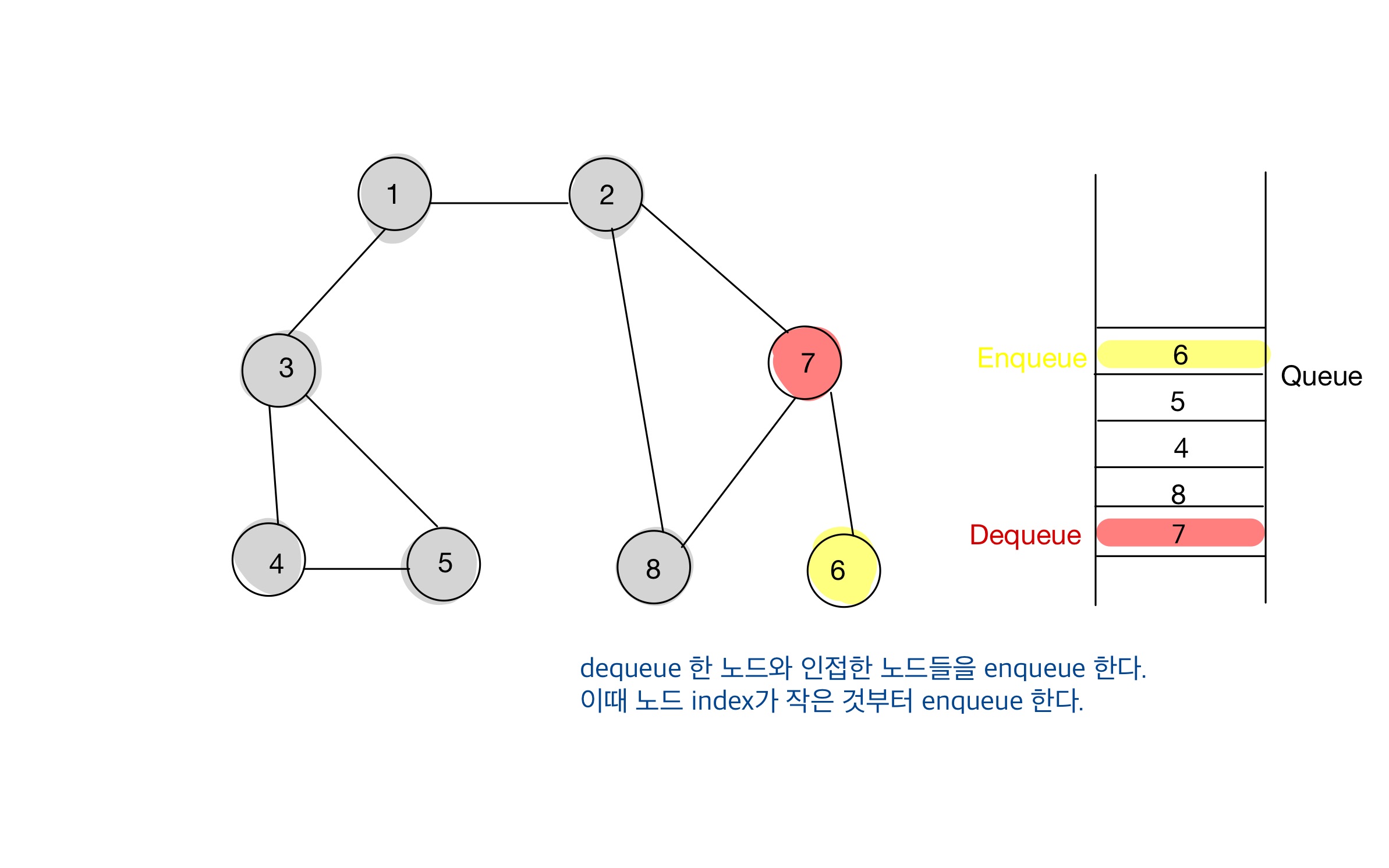
Step 06
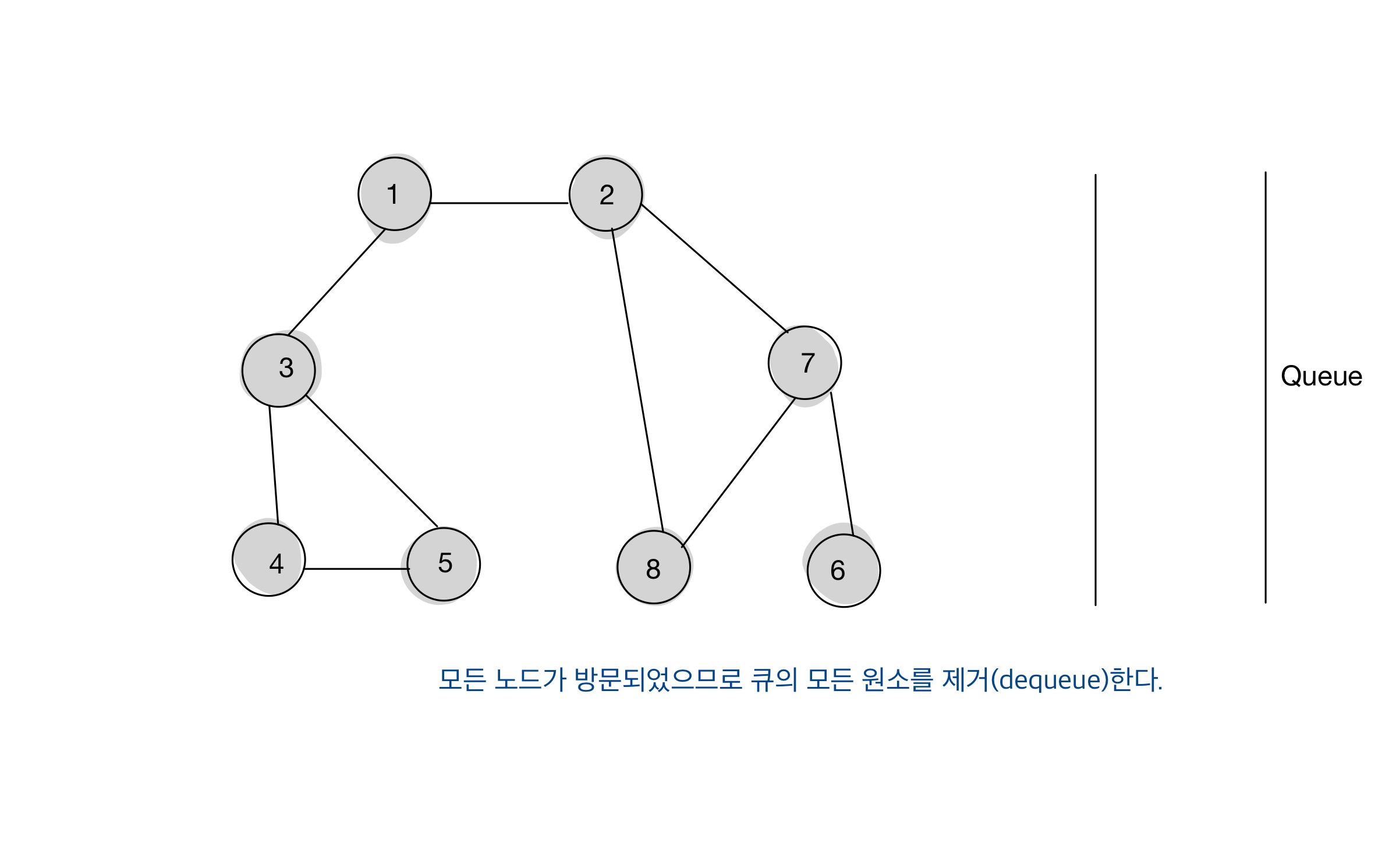
결과
- BFS 수행 결과, 아래 순서대로 탐색되었다.
1 -> 2 -> 3 -> 7 -> 8 -> 4 -> 5 -> 6
특징
- 큐 자료구조에 기초한다는 점에서 구현이 간단하다.
- 탐색을 수행함에 있어
O(n)시간이 소요된다. - 일반적인 경우 실제 수행 시간은 DFS보다 좋은 편이다.
소스코드 - 인접리스트
BFS 알고리즘
public class BFS_ListGraph {
private ArrayList<ArrayList<Integer>> graph; //리스트형 그래프
private boolean[] visitedNode; //방문 노드 표시 (index == 노드번호)
private Deque<Integer> deque = new ArrayDeque<>(); //BFS에서 사용할 큐
private int numbersOfNode; //노드 총 개수
private BFS_ListGraph() {
}
public BFS_ListGraph(ArrayList<ArrayList<Integer>> graph, int numbersOfNode) {
this.graph = graph;
this.numbersOfNode = numbersOfNode;
visitedNode = new boolean[numbersOfNode + 1]; //0번 노드는 없으므로
}
public void solution(int indexOfStartNode) {
//시작 루트 노드 enqueue
deque.addLast(indexOfStartNode);
visitedNode[indexOfStartNode] = true;
System.out.print(indexOfStartNode + " "); //방문 노드 출력
while (!deque.isEmpty()) {
int indexOfDequeuedNode = deque.pollFirst(); //dequeue
ArrayList<Integer> indexOfNearNodes = graph.get(indexOfDequeuedNode); //dequeue 한 노드의 인접 노드들 구하기
//인접 노드들을 enqueue
for (Integer indexOfNearNode : indexOfNearNodes) {
//만약 인접 노드가 방문하지 않은 노드라면 enqueue
if (!visitedNode[indexOfNearNode]) {
deque.addLast(indexOfNearNode); //enqueue
visitedNode[indexOfNearNode] = true; //enqueue 한 노드 방문처리
System.out.print(indexOfNearNode + " "); //방문 노드 출력
}
}
} //while문 종료
}
}
BFS 알고리즘 실행
public class Main {
/**
* BFS 실행 메서드
*/
public static void execute() {
int numbersOfNode = 8; //총 노드 개수
//그래프 초기화 (노드는 1번부터 시작한다.)
ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
for (int i = 0; i <= numbersOfNode; i++) {
graph.add(new ArrayList<Integer>());
}
//--- 그래프 작성 ---
graph.get(1).add(2); //'1번 노드'와 인접한(연결된) 노드로 '2번 노드' 등록
graph.get(1).add(3); //'1번 노드'와 인접한(연결된) 노드로 '3번 노드' 등록
graph.get(2).add(1); //'2번 노드'와 인접한(연결된) 노드로 '1번 노드' 등록
graph.get(2).add(7); //'2번 노드'와 인접한(연결된) 노드로 '7번 노드' 등록
graph.get(2).add(8); //'2번 노드'와 인접한(연결된) 노드로 '8번 노드' 등록
graph.get(3).add(1); //'3번 노드'와 인접한(연결된) 노드로 '1번 노드' 등록
graph.get(3).add(4); //'3번 노드'와 인접한(연결된) 노드로 '4번 노드' 등록
graph.get(3).add(5); //'3번 노드'와 인접한(연결된) 노드로 '5번 노드' 등록
graph.get(4).add(3); //'4번 노드'와 인접한(연결된) 노드로 '3번 노드' 등록
graph.get(4).add(5); //'4번 노드'와 인접한(연결된) 노드로 '5번 노드' 등록
graph.get(5).add(3); //'5번 노드'와 인접한(연결된) 노드로 '3번 노드' 등록
graph.get(5).add(4); //'5번 노드'와 인접한(연결된) 노드로 '4번 노드' 등록
graph.get(6).add(7); //'6번 노드'와 인접한(연결된) 노드로 '7번 노드' 등록
graph.get(7).add(2); //'7번 노드'와 인접한(연결된) 노드로 '2번 노드' 등록
graph.get(7).add(6); //'7번 노드'와 인접한(연결된) 노드로 '6번 노드' 등록
graph.get(7).add(8); //'7번 노드'와 인접한(연결된) 노드로 '8번 노드' 등록
graph.get(8).add(1); //'8번 노드'와 인접한(연결된) 노드로 '1번 노드' 등록
graph.get(8).add(7); //'8번 노드'와 인접한(연결된) 노드로 '7번 노드' 등록
//----- 그래프 작성 끝 -----
//BFS 알고리즘 시작
BFS_ListGraph bfs = new BFS_ListGraph(graph, numbersOfNode);
bfs.solution(1);
}
}
본 소스코드의
graph는 위 그림 예시에서 사용한 그래프와 동일한 것이다.
출력결과
1 2 3 7 8 4 5 6
소스코드 - 인접행렬
BFS 알고리즘
public class BFS_MatrixGraph {
boolean[][] graph;
boolean[] visitedNode;
int numbersOfNodes;
Deque<Integer> deque = new ArrayDeque<>();
private BFS_MatrixGraph() {}
public BFS_MatrixGraph(boolean[][] graph, int numbersOfNodes) {
this.graph = graph;
this.numbersOfNodes = numbersOfNodes;
this.visitedNode = new boolean[numbersOfNodes+1]; //노드는 1번부터 시작하므로
}
public void solution(int indexOfStartNode) {
deque.addLast(indexOfStartNode); //시작 루트 노드 enqueue
visitedNode[indexOfStartNode] = true; //시작 루트 노드 방문 표시 (index == 노드번호)
System.out.print(indexOfStartNode + " "); //방문노드 출력
while (!deque.isEmpty()) {
int indexOfDequeuedNode = deque.pollFirst(); //dequeue
//dequeue 한 노드의 인접 노드 구하기
boolean[] indexOfNearNodes = graph[indexOfDequeuedNode];
for (int i = 1; i < indexOfNearNodes.length; i++) {
if (indexOfNearNodes[i]) { //만약 i번 노드가 dequeue된 노드와 인접한다면
if (!visitedNode[i]) { //만약 i번 노드가 미방문 상태라면
deque.addLast(i); //인접노드 enqueue
visitedNode[i] = true; //방문 표시
System.out.print(i + " "); //방문 노드 출력
}
}
} //for문 종료
} //while문 종료
}
}
BFS 알고리즘 실행
public class Main {
/**
* 실행 메서드
*/
public static void execute() {
int numberOfNode = 8; //총 노드 개수
//graph (true면 인접)
boolean[][] graph = new boolean[][] {
{false, false, false, false, false, false, false, false, false},
{false, false, true, true, false, false, false, false, false},
{false, true, false, false, false, false, false, true, true},
{false, true, false, false, true, true, false, false, false},
{false, false, false, true, false, true, false, false, false},
{false, false, false, true, true, false, false, false, false},
{false, false, false, false, false, false, false, true, false},
{false, false, true, false, false, false, true, false, true},
{false, false, true, false, false, false, false, true, false}
};
BFS_MatrixGraph bfs = new BFS_MatrixGraph(graph, numberOfNode);
bfs.solution(1);
}
}
본 소스코드의
graph는 위 그림 예시에서 사용한 그래프와 동일한 것이다.
- 모든 첫번째 행과, 모든 첫번째 열은 false로 처리했다. (노드가 1부터 시작하므로)
graph[A][A]와 같이 자기자신을 의미하는 index의 경우, false로 처리했다.- true: 해당 노드끼리 인접한다.
- false: 해당 노드끼리 인접하지 않는다.
- 예시
graph[4][5] = true: ‘노드4’와 ‘노드5’가 인접한다.graph[7][1] = false: ‘노드7’과 ‘노드1’은 인접하지 않는다.
출력결과
1 2 3 7 8 4 5 6
소스코드 흐름
인접리스트 방식과 동일하다.
Tip
- 그래프 탐색 문제에서 가장 가까운, 최소 등 이 핵심이라면, 주로 BFS를 사용한다.
- 나동빈, 『이것이 코딩 테스트다』
