DFS : 개념
개요
DFS란?
- Depth First Search의 약자로, 깊이 우선 탐색 알고리즘이다.
- 그래프 구조에서 탐색을 위해 사용되는 탐색 알고리즘이다.
- 그래프의 모든 노드들을 방문(탐색)해야 한다.
- 특정한 경로로 탐색을 하다가 특정한 상황에서 최대한 깊숙이 들어가 노드를 방문한 후, 다시 돌아가 다른 경로로 탐색하는 알고리즘이다.
DFS 동작 과정
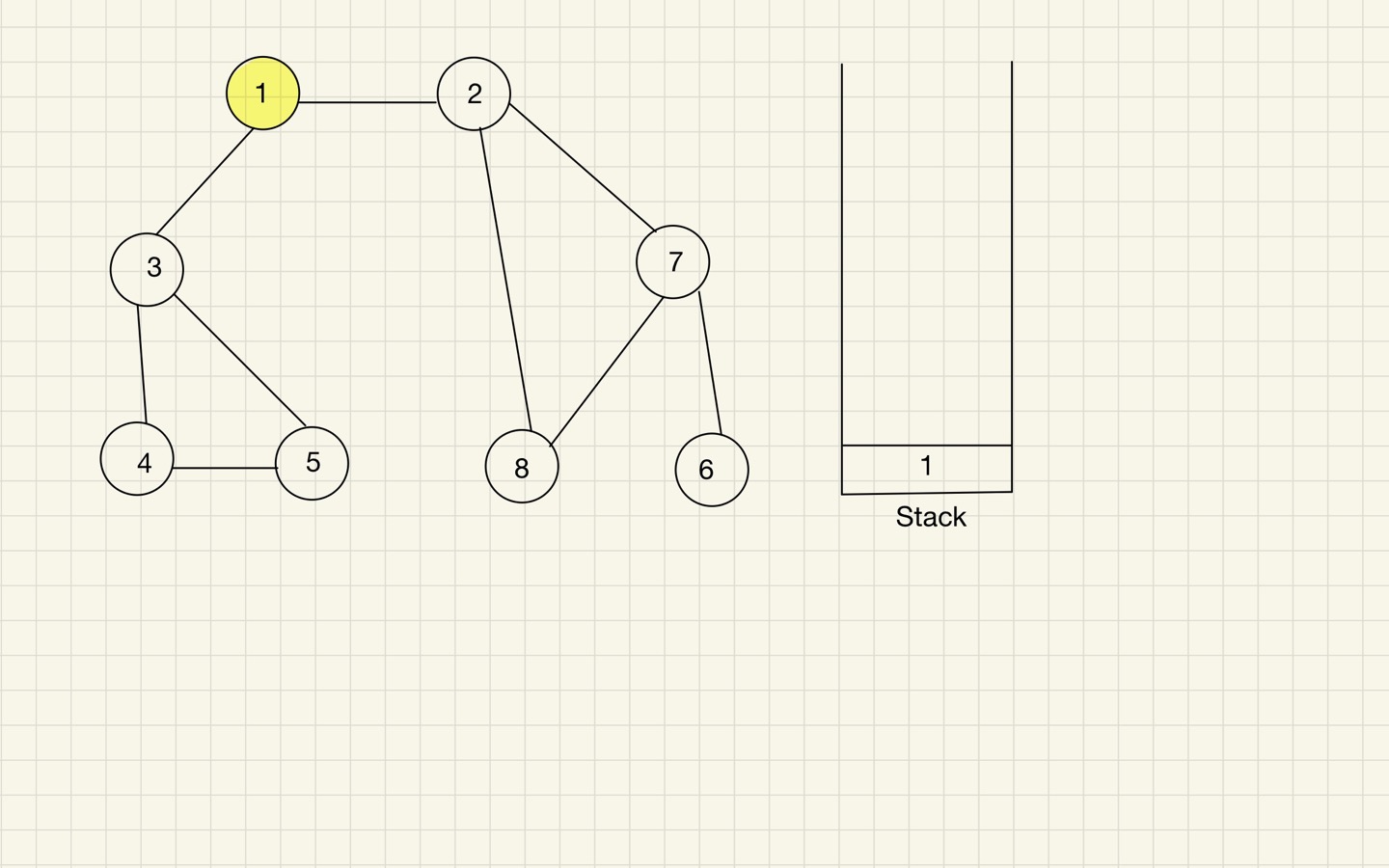
- 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
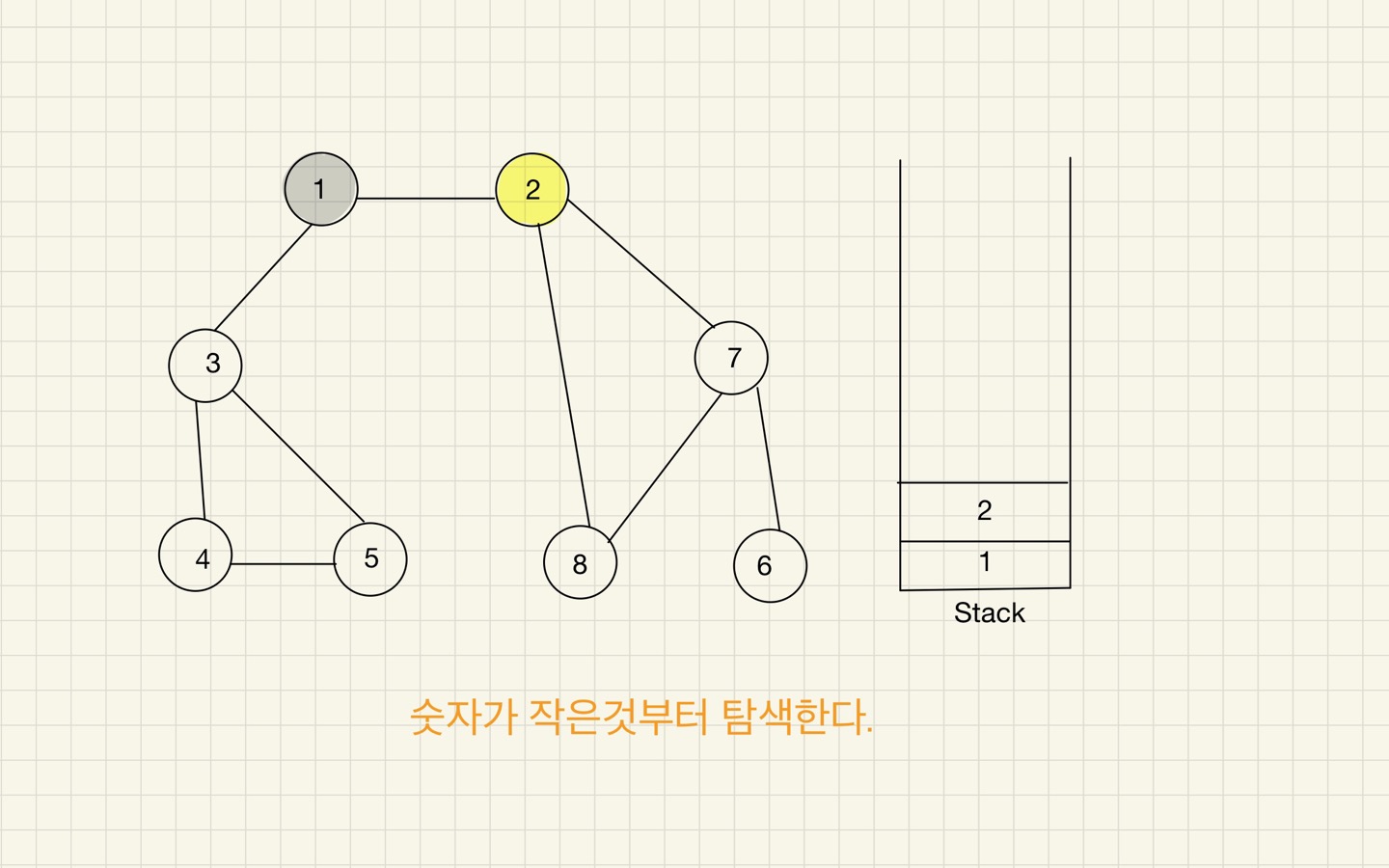
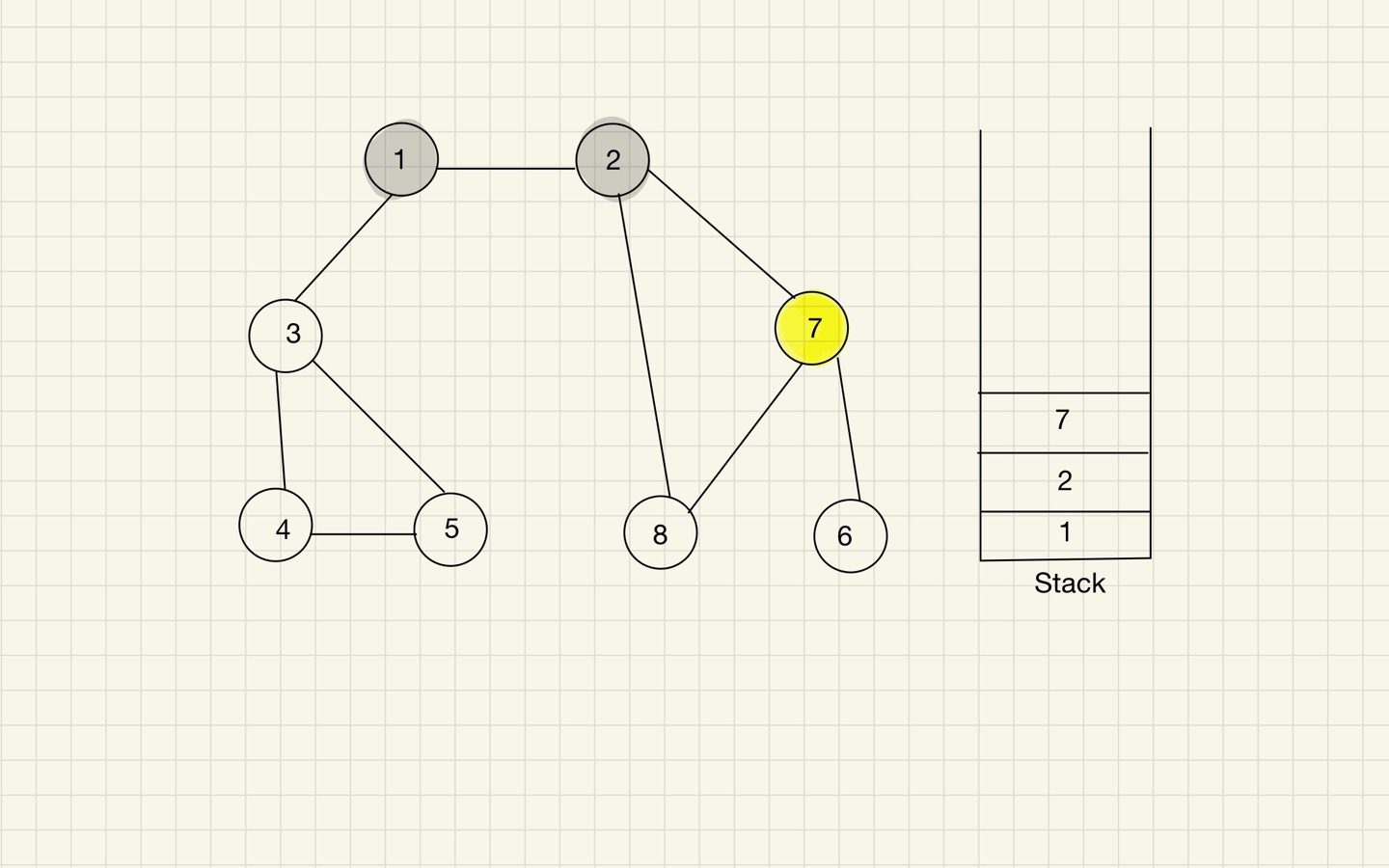
- 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리를 한다.
방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다. - 2번 과정을 더 이상 수행할 수 없을 때까지 반복한다.
DFS에서 인접 노드를 선택할 땐, 가장 낮은 번호를 갖는 노드를 최우선으로 선택하는 것이 좋다.
예시
예시에서 사용할 그래프 형태
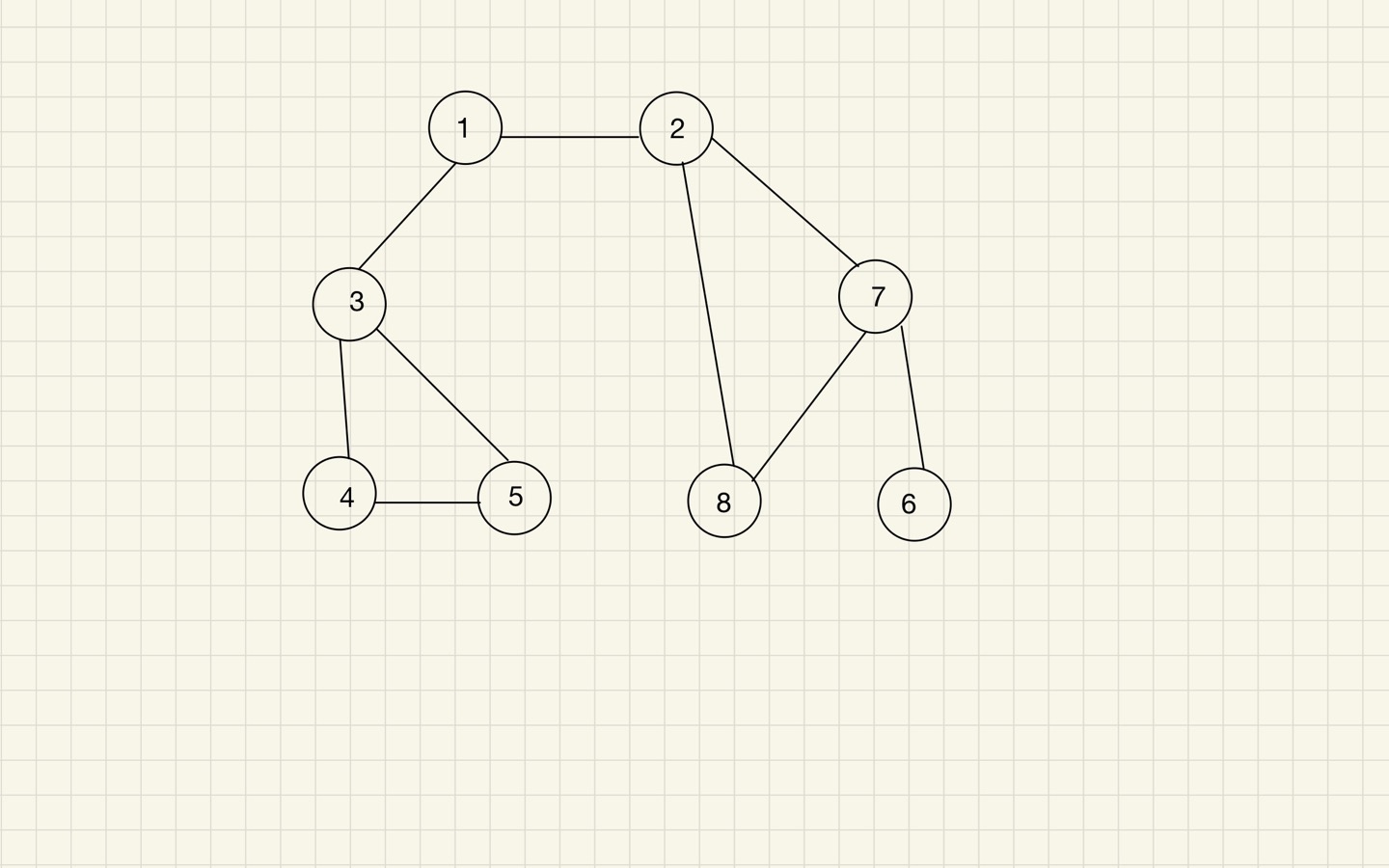
8번 노드가 1번 노드가 아닌 2번 노드와 인접함에 주의하자!
(교재와 다르다.)
Step 01
Step 02
Step 03
Step 04
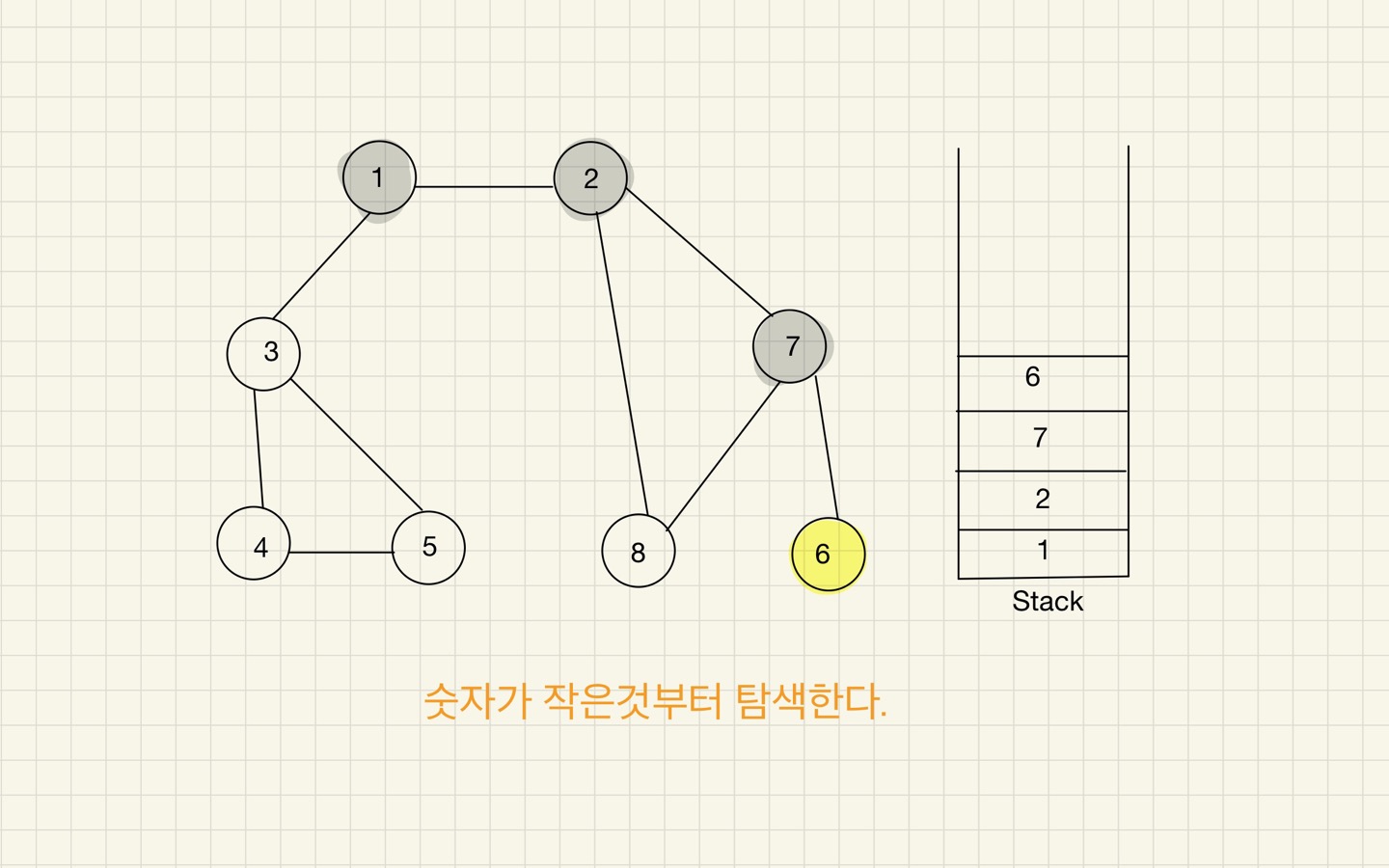
Step 05
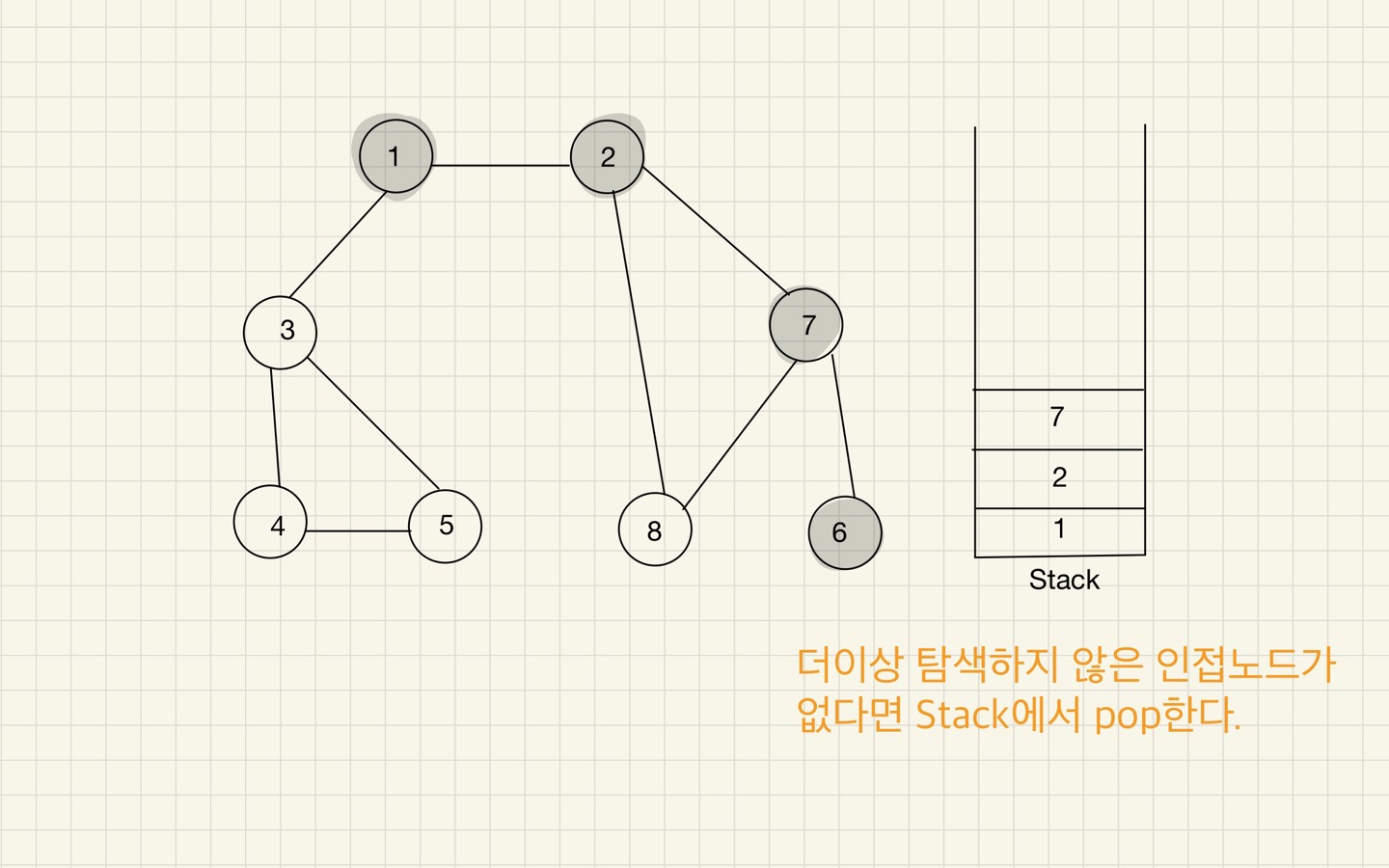
Step 06
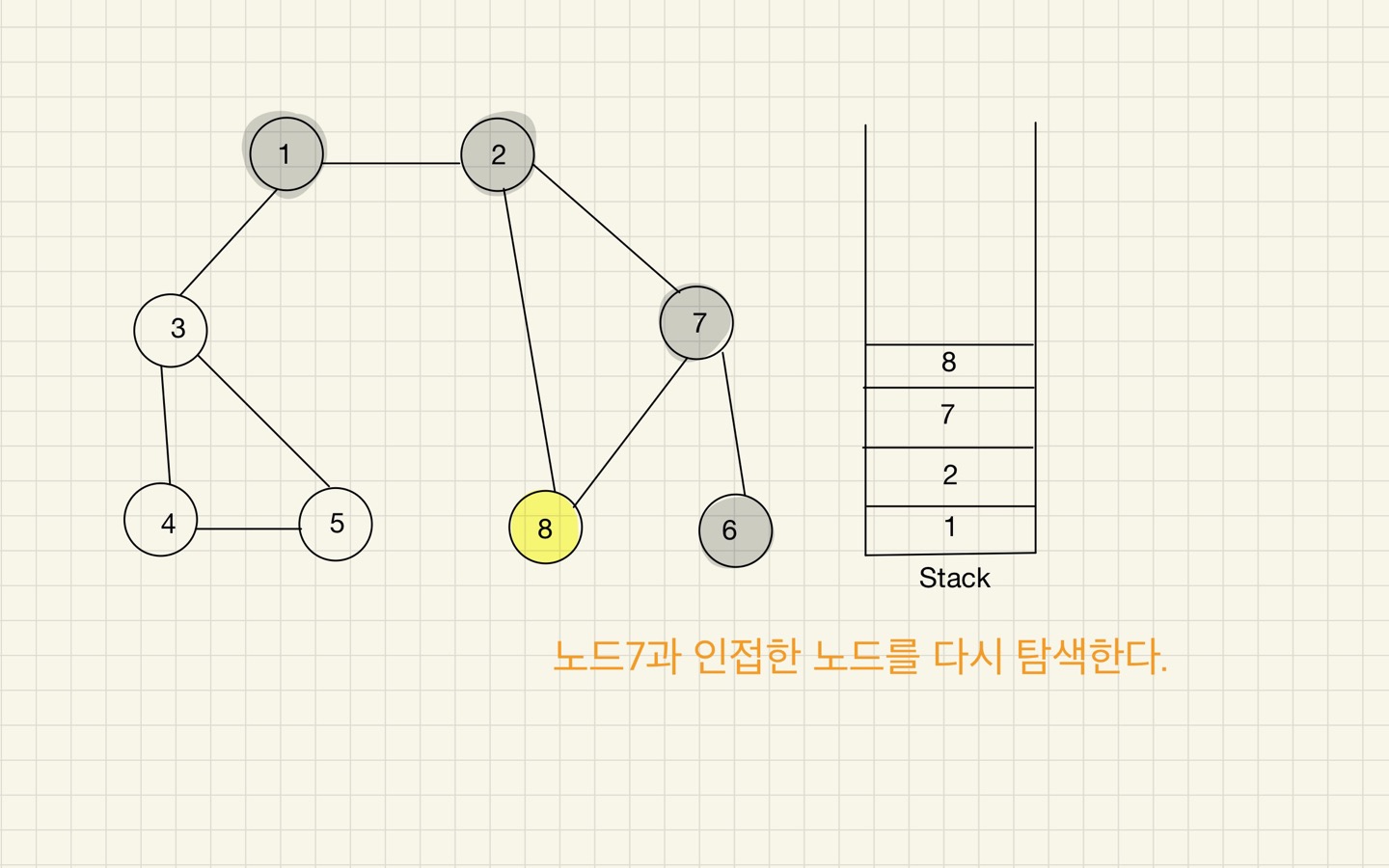
Step 07
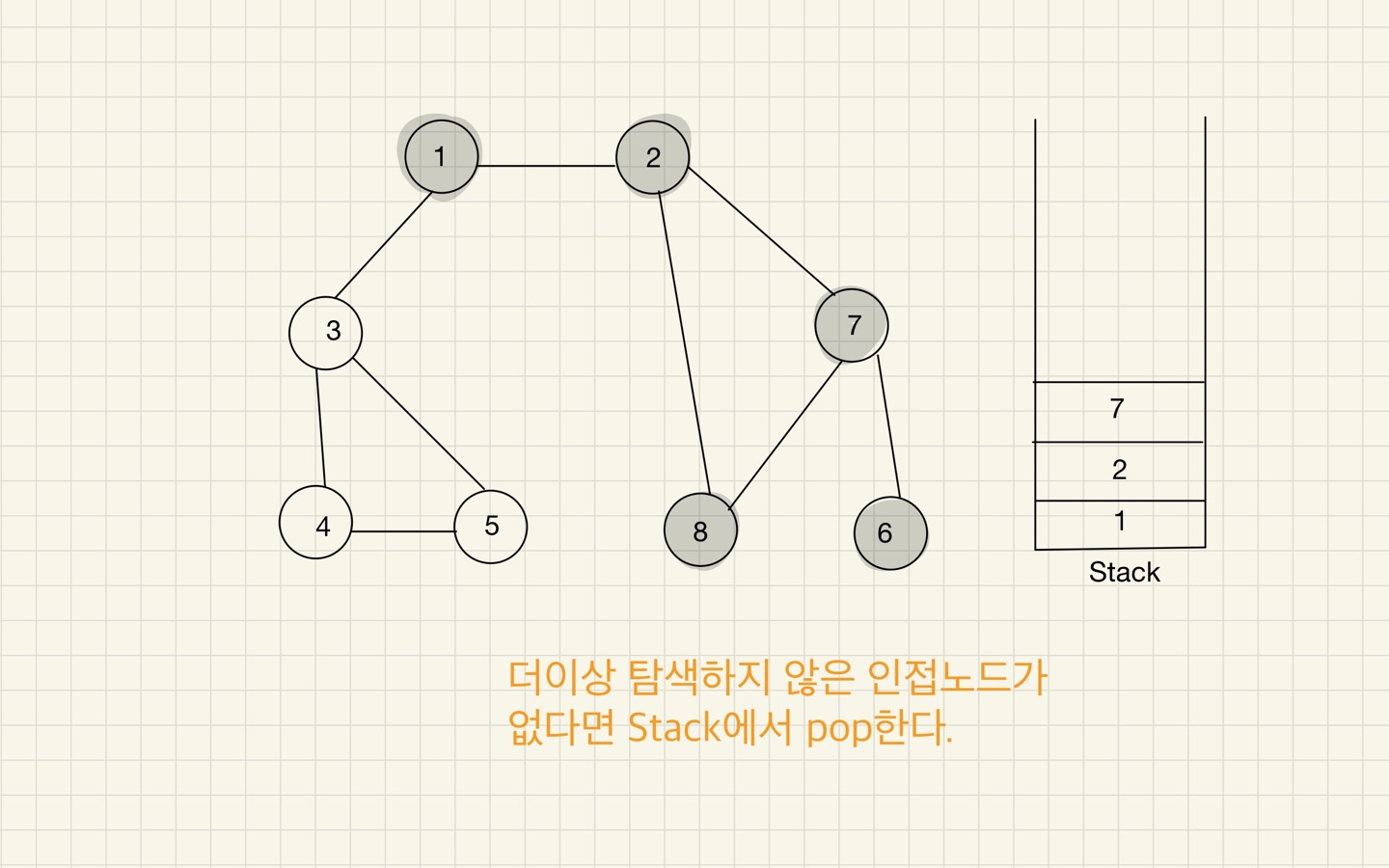
Step 08
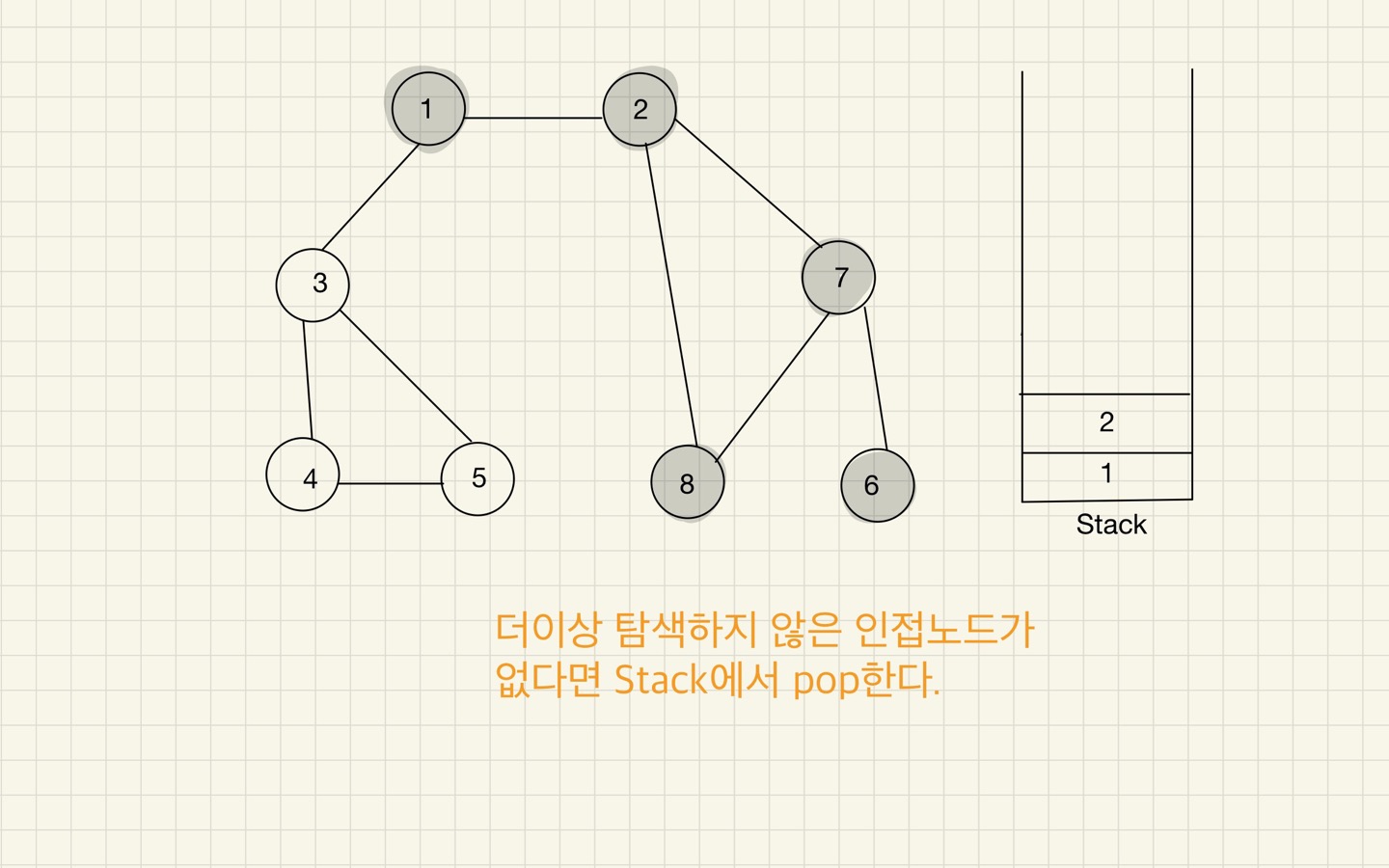
Step 09
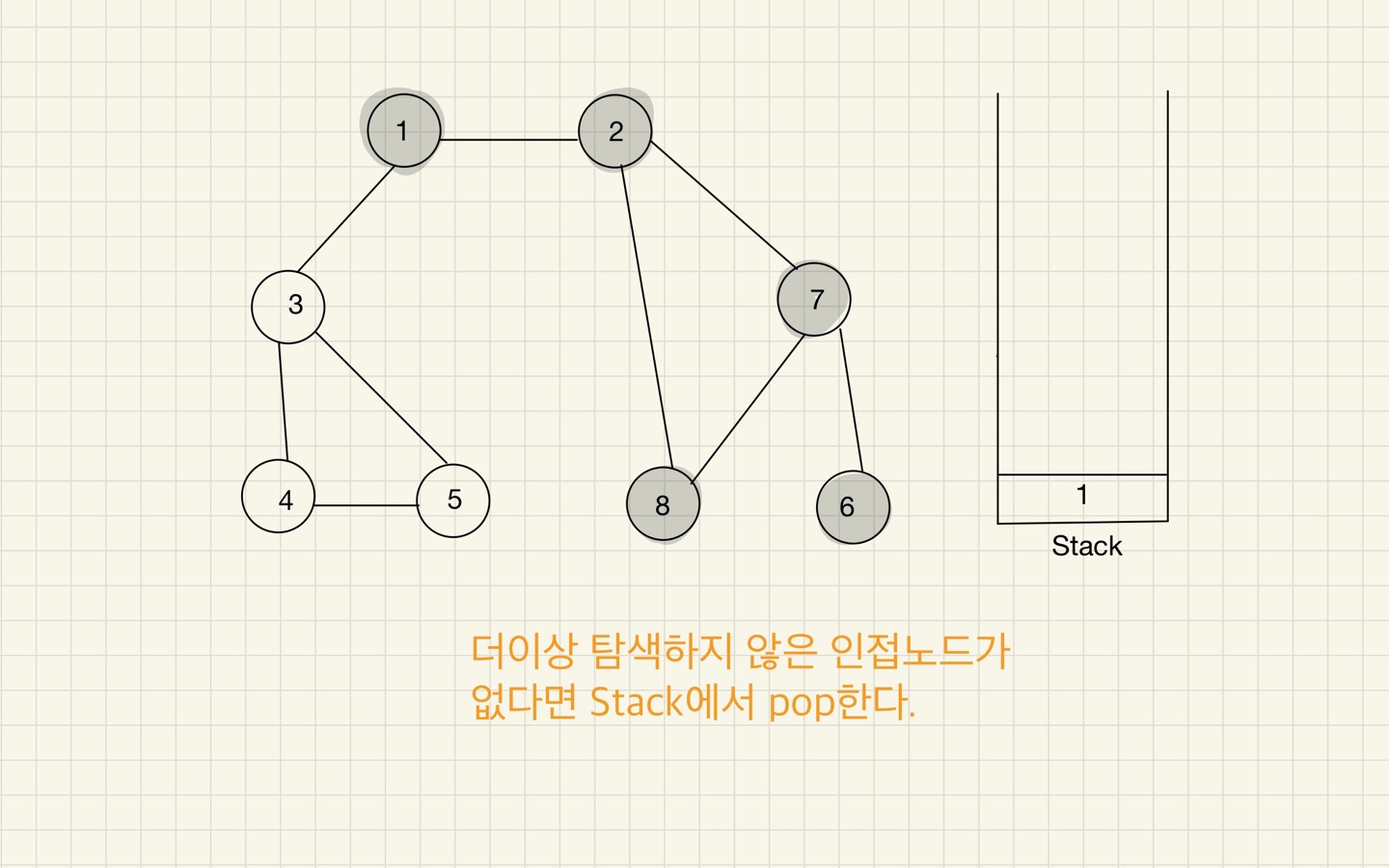
Step 10
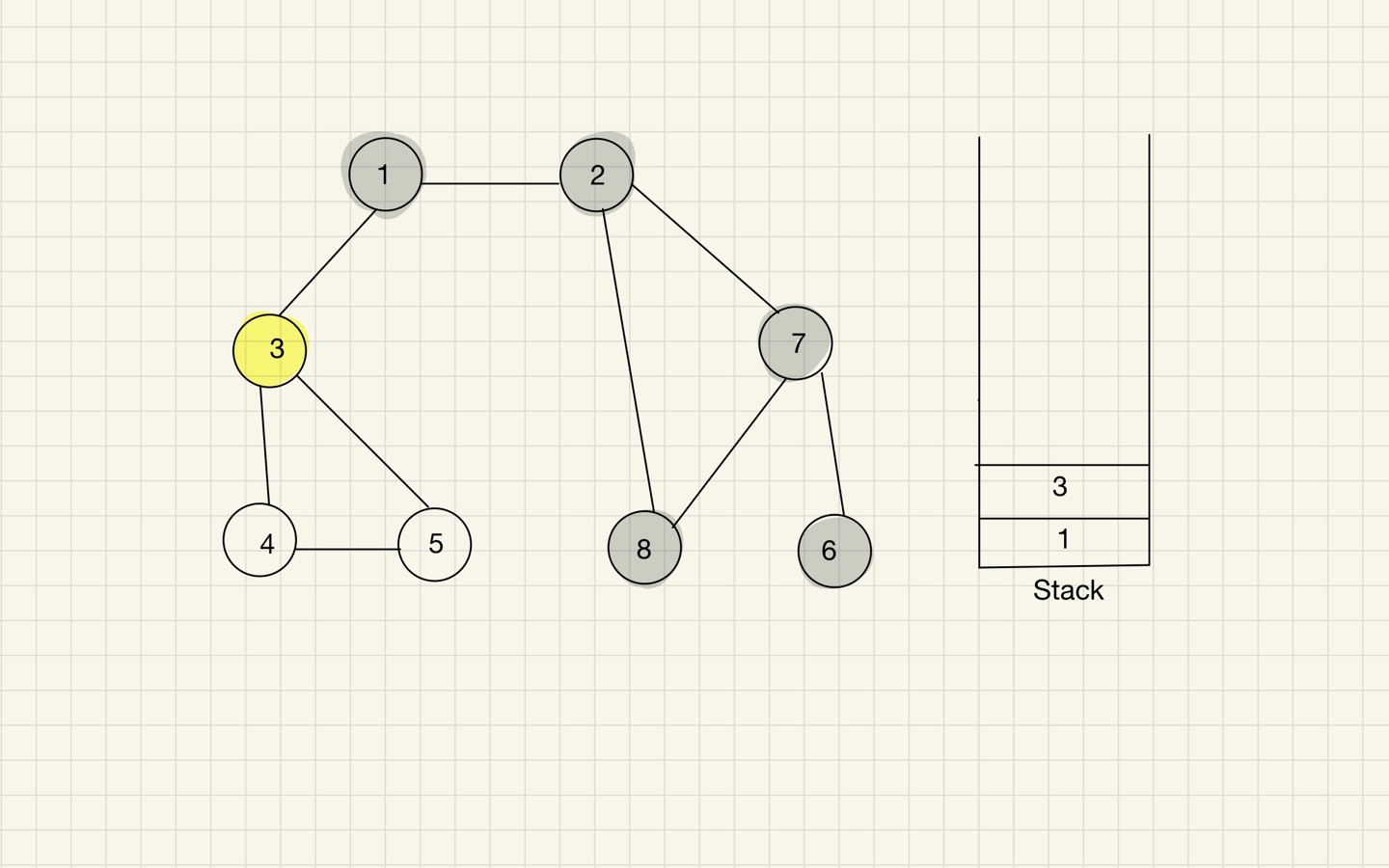
Step 11
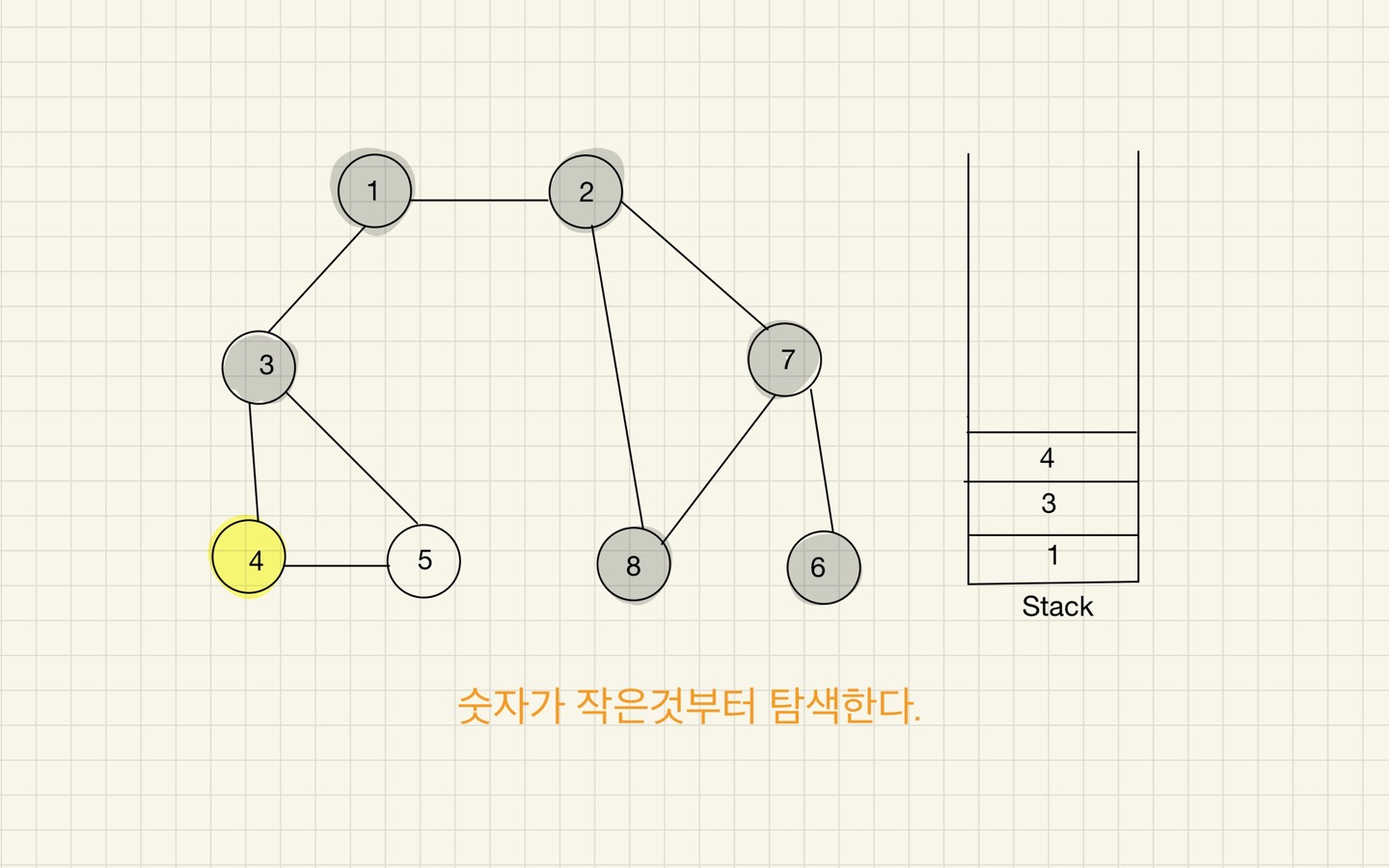
Step 12
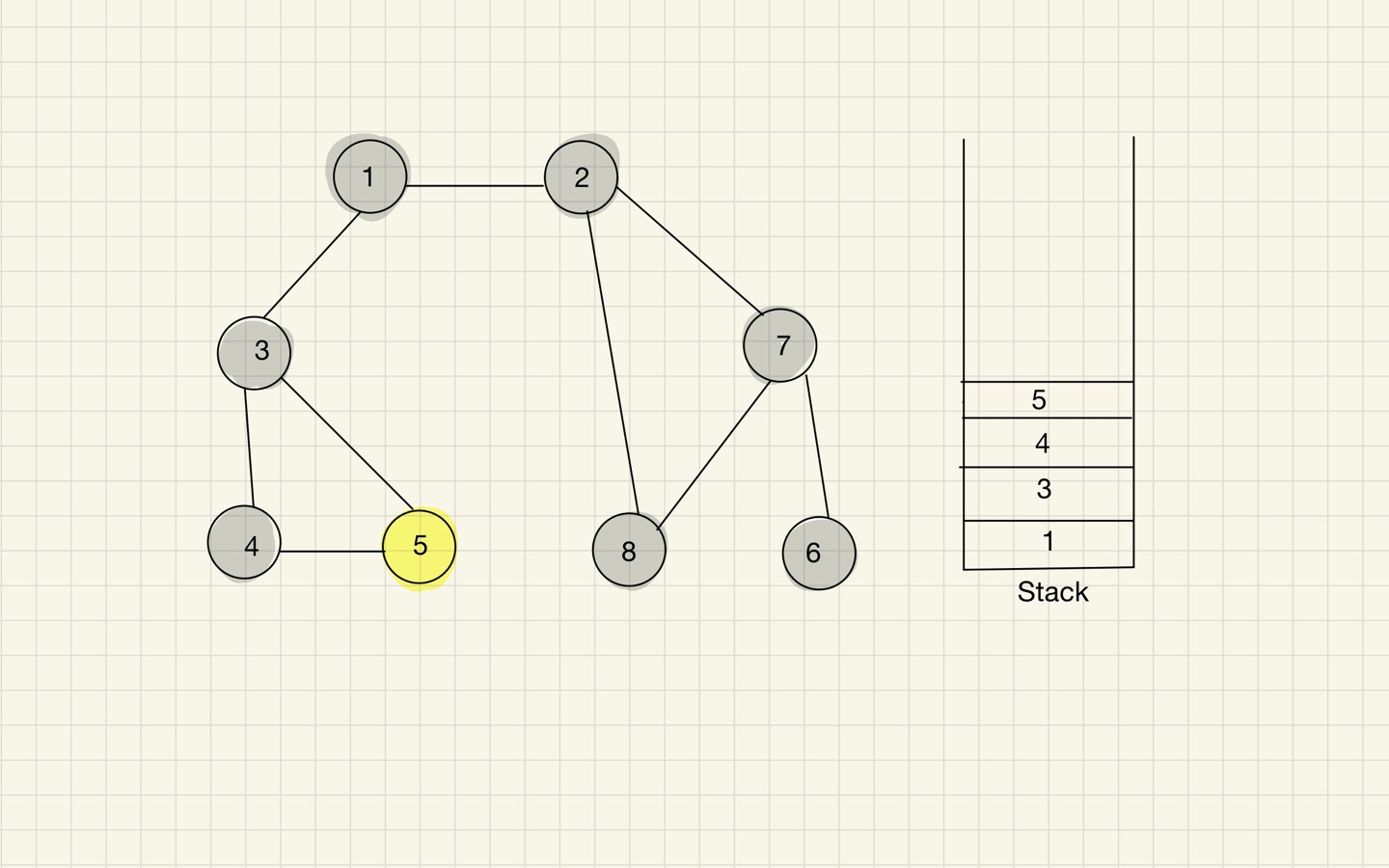
Step 13
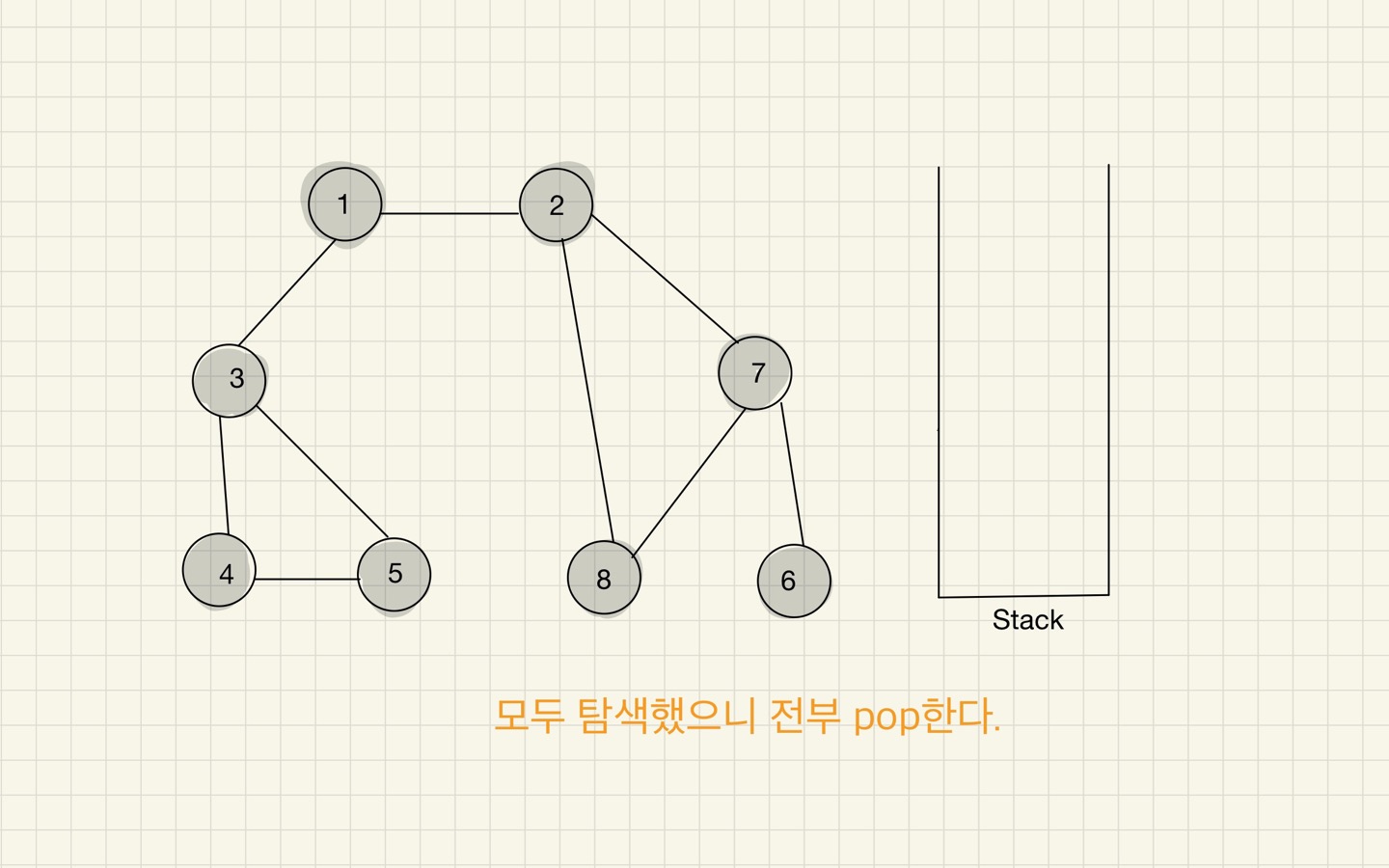
결과
- DFS 수행 결과, 아래 순서대로 탐색되었다.
1 -> 2 -> 7 -> 6 -> 8 -> 3 -> 4 -> 5
특징
- stack 대신 재귀 함수를 이용하여, DFS를 구현할 수 있다.
소스코드 - 인접리스트
DFS 알고리즘
public class DFS_ListGraph {
//리스트형 그래프
private ArrayList<ArrayList<Integer>> graph;
private boolean[] visitedNode; //배열의 index == 노드번호
private DFS_ListGraph() {
}
public DFS_ListGraph(ArrayList<ArrayList<Integer>> graph, int numbersOfNode) {
this.graph = graph;
visitedNode = new boolean[numbersOfNode+1]; //0번 index를 갖는 노드는 생략할 것이기 때문에
}
public void solution(int indexOfNowNode) {
//현재 방문한 노드(indexOfNowNode)를 방문 처리
visitedNode[indexOfNowNode] = true;
//현재 방문한 노드 출력
System.out.print(indexOfNowNode + " ");
//현재 방문한 노드(indexOfNowNode)의 인접노드들
ArrayList<Integer> nearNodesOfNowNode = graph.get(indexOfNowNode);
for (int i = 0; i < nearNodesOfNowNode.size(); i++) {
int indexOfNearNode = nearNodesOfNowNode.get(i);
if (!visitedNode[indexOfNearNode]) {
solution(indexOfNearNode);
}
}
}
}
DFS 알고리즘 실행
public class Main {
/**
* DFS 실행 메서드
*/
public static void execute() {
int numbersOfNode = 8; //노드 총 개수
ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
//그래프 초기화
for (int i = 0; i <= numbersOfNode; i++) {
graph.add(new ArrayList<>());
}
//------- 그래프 만들기 (노드는 1번부터 시작한다.) -----
graph.get(1).add(2); //'1번 노드'와 인접한(연결된) 노드로 '2번 노드' 등록
graph.get(1).add(3); //'1번 노드'와 인접한(연결된) 노드로 '3번 노드' 등록
graph.get(2).add(1); //'2번 노드'와 인접한(연결된) 노드로 '1번 노드' 등록
graph.get(2).add(7); //'2번 노드'와 인접한(연결된) 노드로 '7번 노드' 등록
graph.get(2).add(8); //'2번 노드'와 인접한(연결된) 노드로 '8번 노드' 등록
graph.get(3).add(1); //'3번 노드'와 인접한(연결된) 노드로 '1번 노드' 등록
graph.get(3).add(4); //'3번 노드'와 인접한(연결된) 노드로 '4번 노드' 등록
graph.get(3).add(5); //'3번 노드'와 인접한(연결된) 노드로 '5번 노드' 등록
graph.get(4).add(3); //'4번 노드'와 인접한(연결된) 노드로 '3번 노드' 등록
graph.get(4).add(5); //'4번 노드'와 인접한(연결된) 노드로 '5번 노드' 등록
graph.get(5).add(3); //'5번 노드'와 인접한(연결된) 노드로 '3번 노드' 등록
graph.get(5).add(4); //'5번 노드'와 인접한(연결된) 노드로 '4번 노드' 등록
graph.get(6).add(7); //'6번 노드'와 인접한(연결된) 노드로 '7번 노드' 등록
graph.get(7).add(2); //'7번 노드'와 인접한(연결된) 노드로 '2번 노드' 등록
graph.get(7).add(6); //'7번 노드'와 인접한(연결된) 노드로 '6번 노드' 등록
graph.get(7).add(8); //'7번 노드'와 인접한(연결된) 노드로 '8번 노드' 등록
graph.get(8).add(2); //'8번 노드'와 인접한(연결된) 노드로 '2번 노드' 등록
graph.get(8).add(7); //'8번 노드'와 인접한(연결된) 노드로 '7번 노드' 등록
//----- 그래프 만들기 끝 -----
//DFS 알고리즘 시작
DFS_ListGraph dfs = new DFS_ListGraph(graph, numbersOfNode);
dfs.solution(1); //루트 노드부터 시작
}
}
본 소스코드의
graph는 위 그림 예시에서 사용한 그래프와 동일한 것이다.
출력결과
1 2 7 6 8 3 4 5
소스코드 흐름
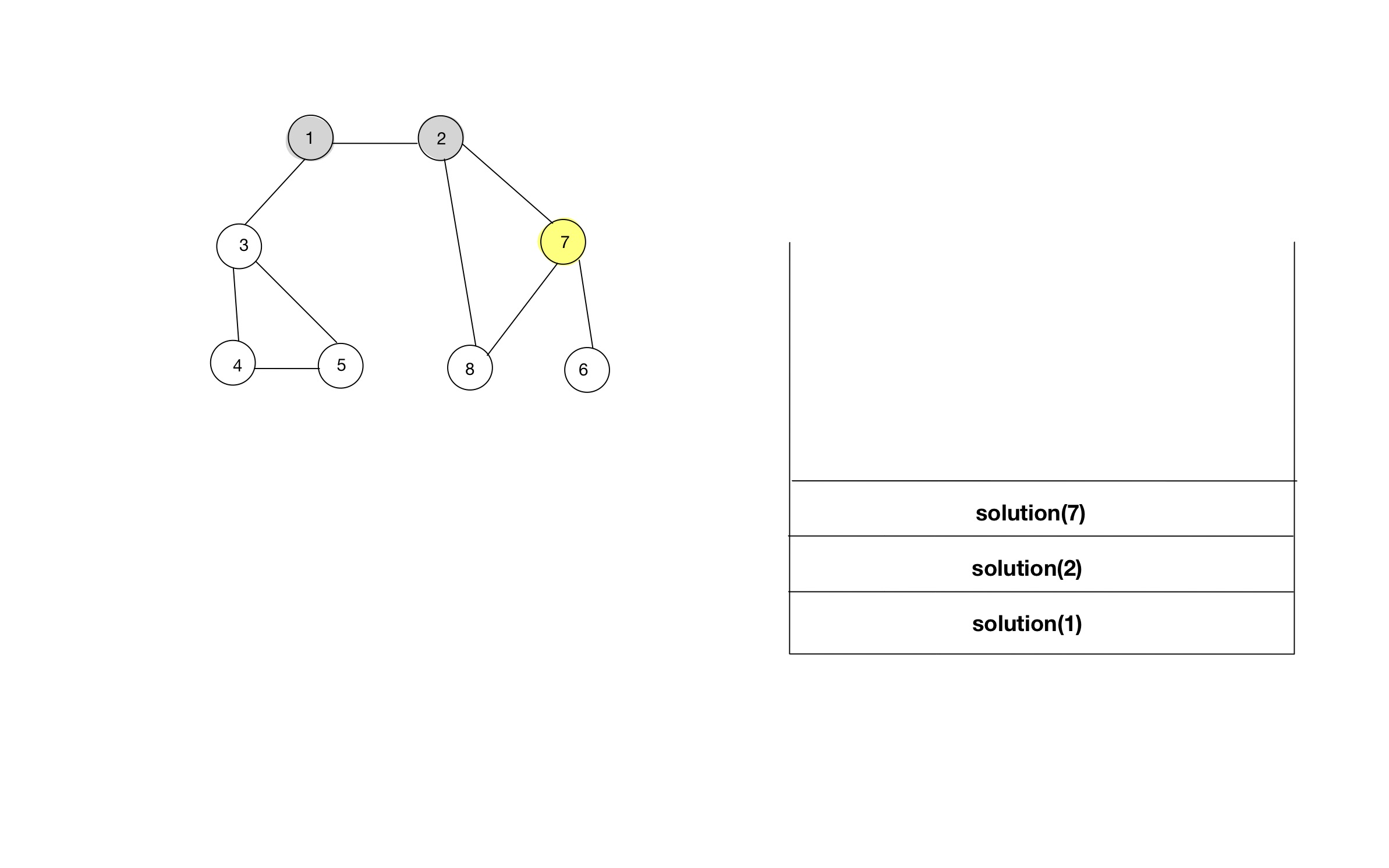
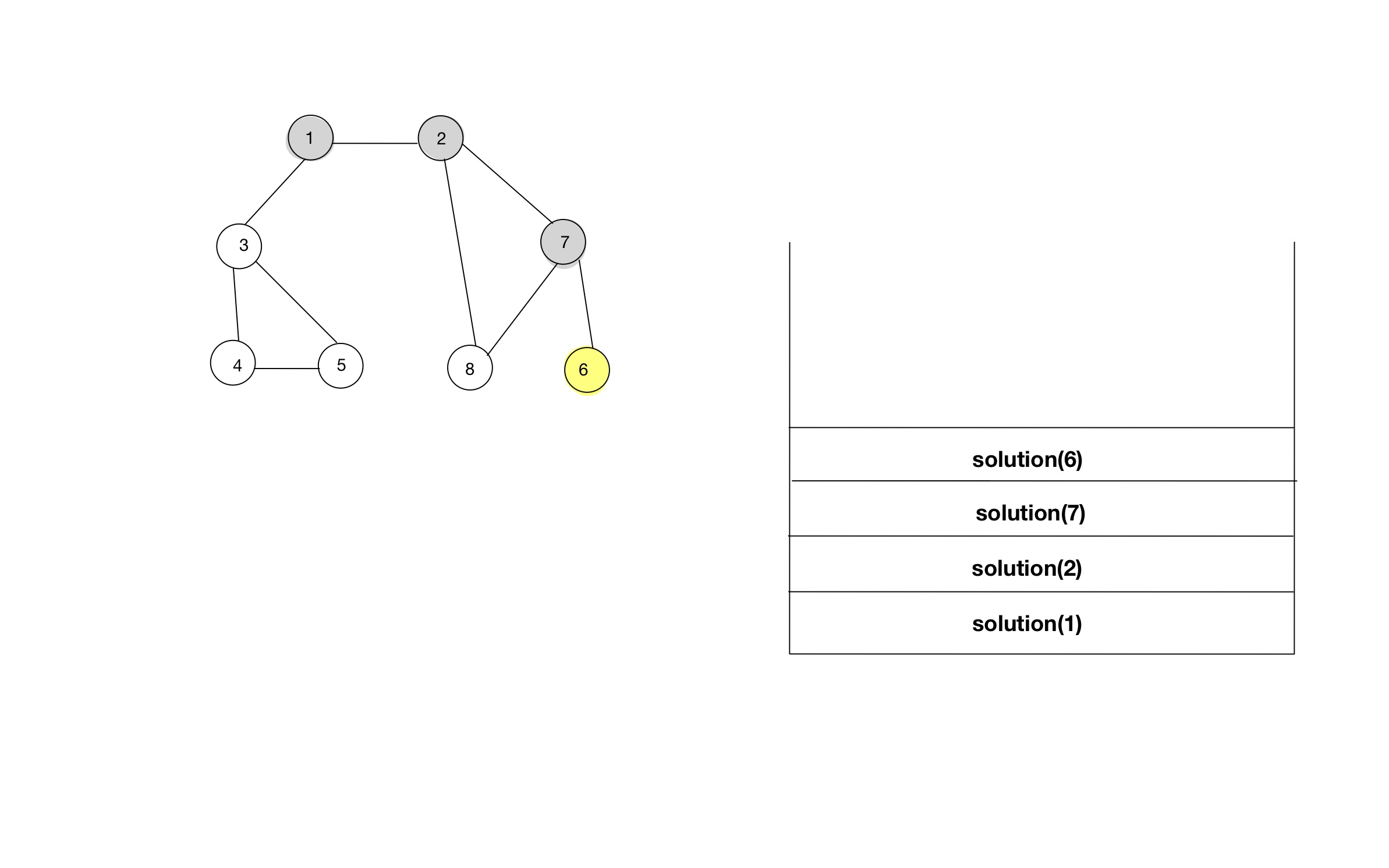
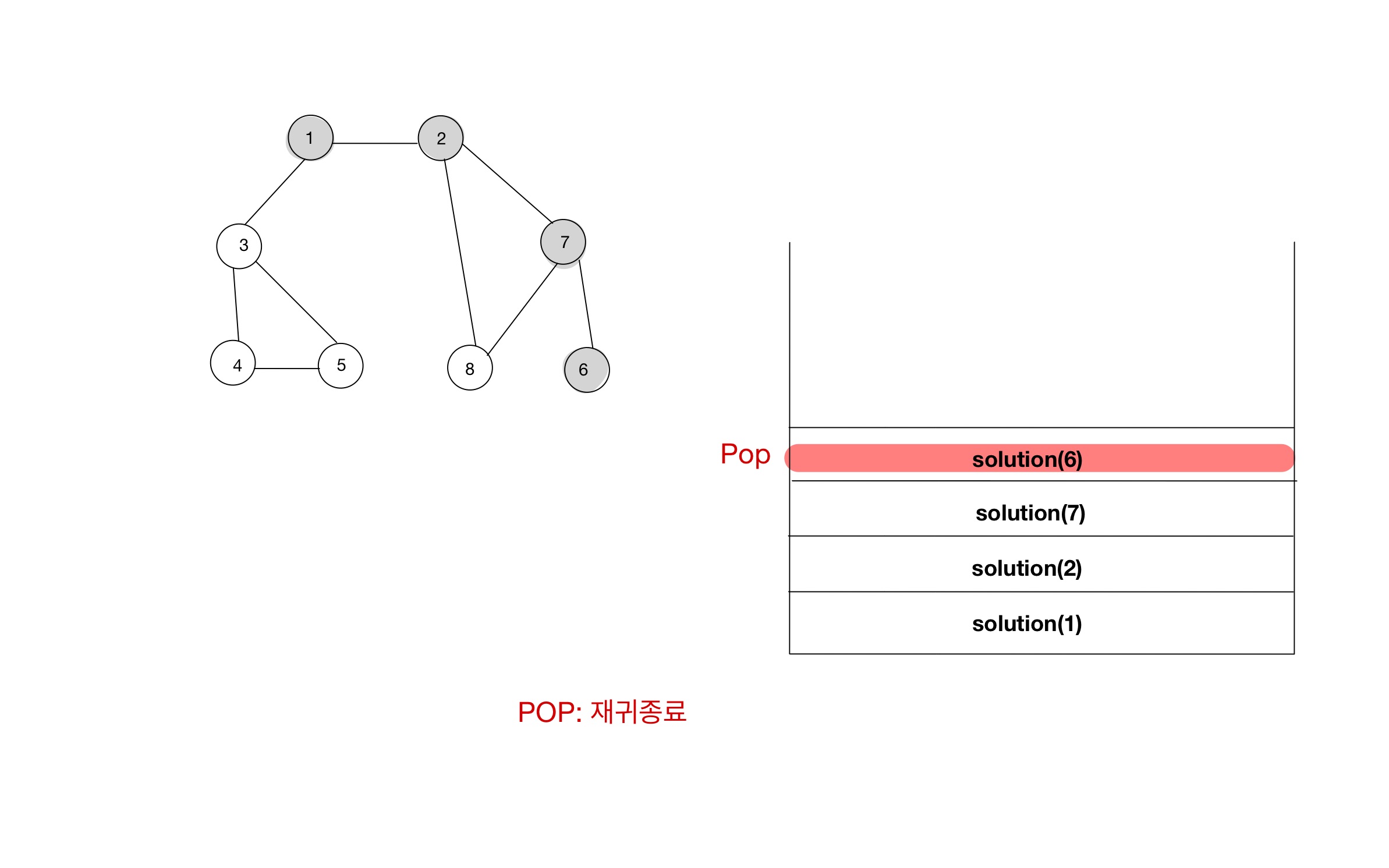
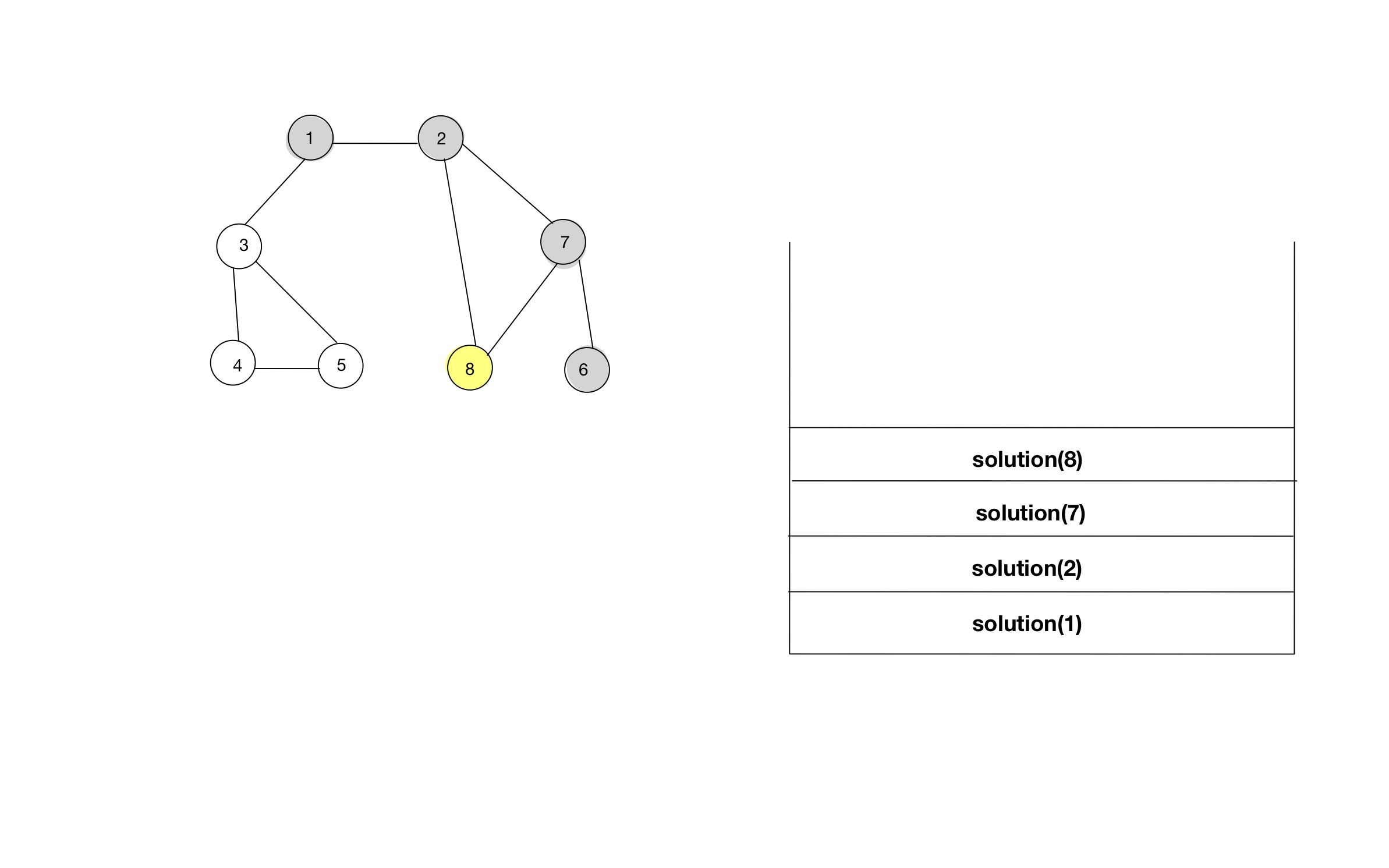
- 함수 호출스택을 통해, 소스코드가 어떻게 동작하는지 알아보자.
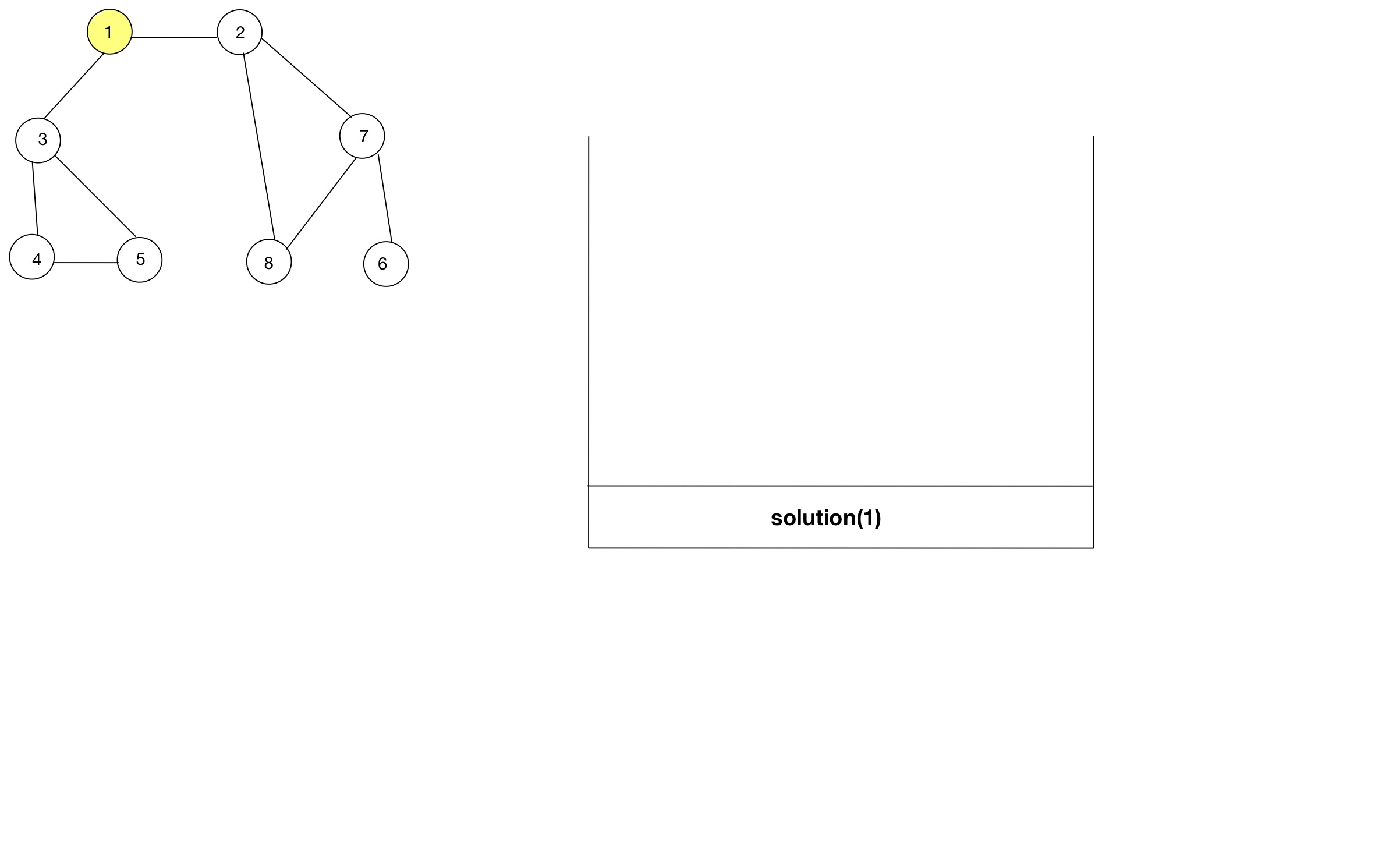
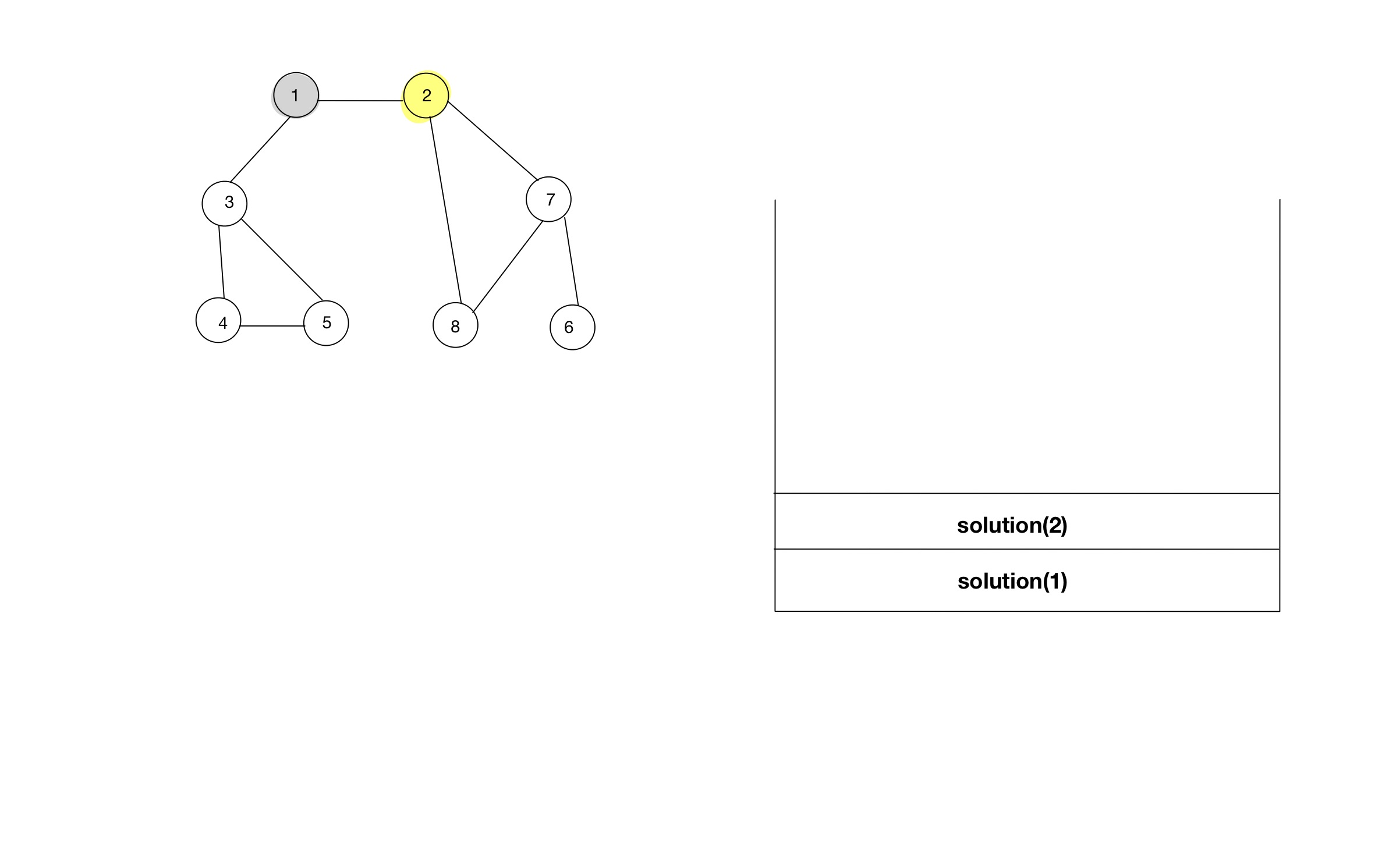
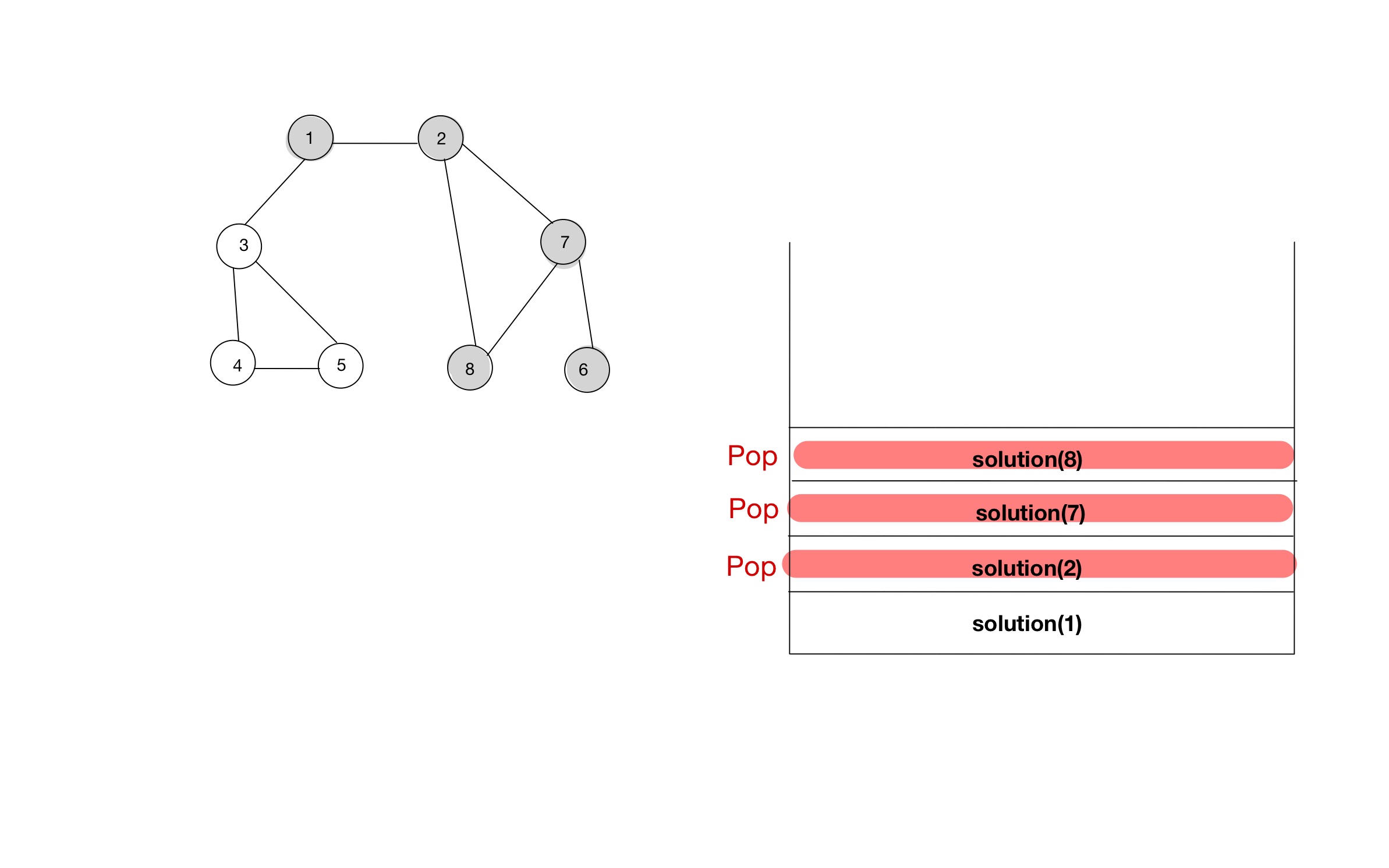
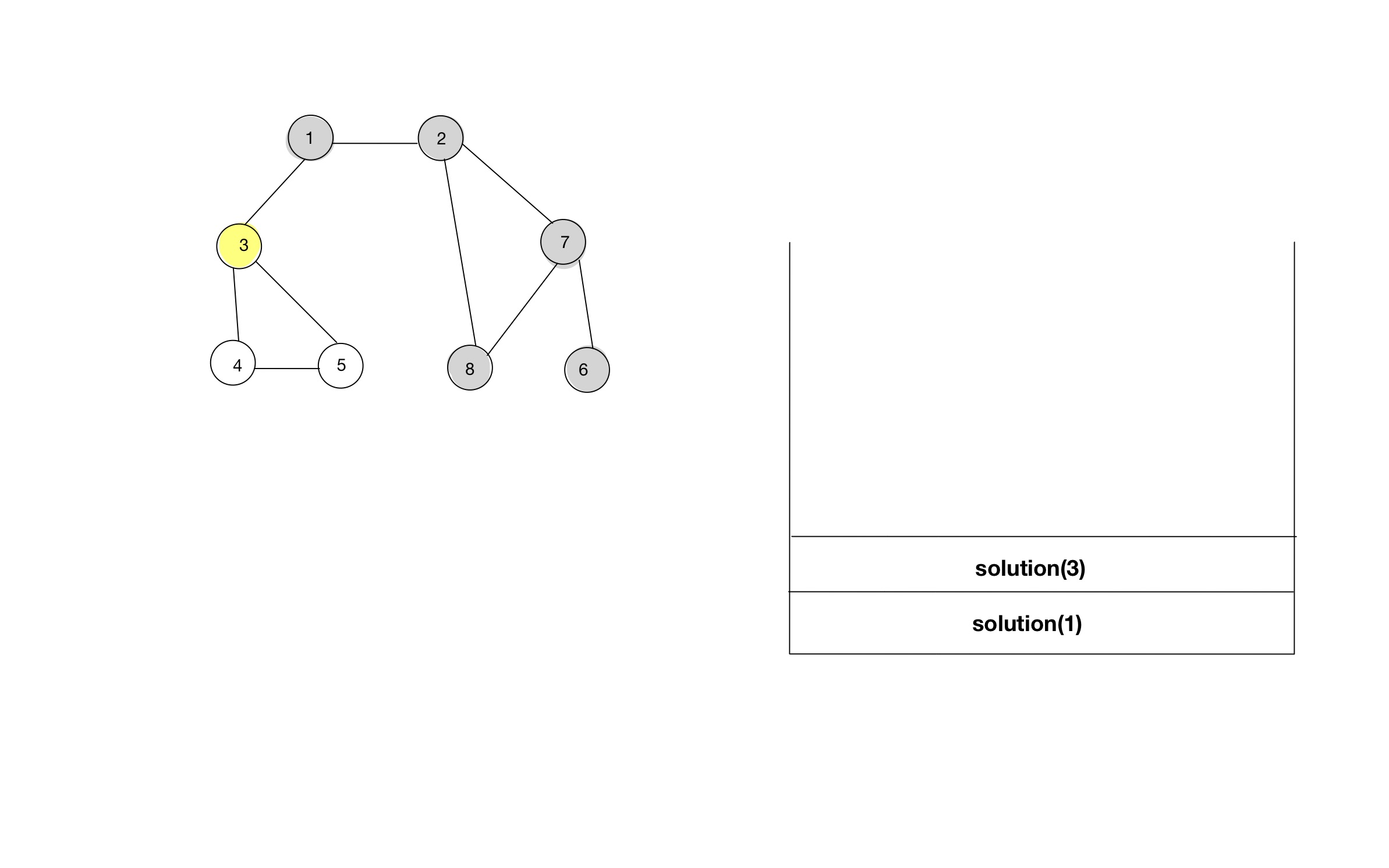
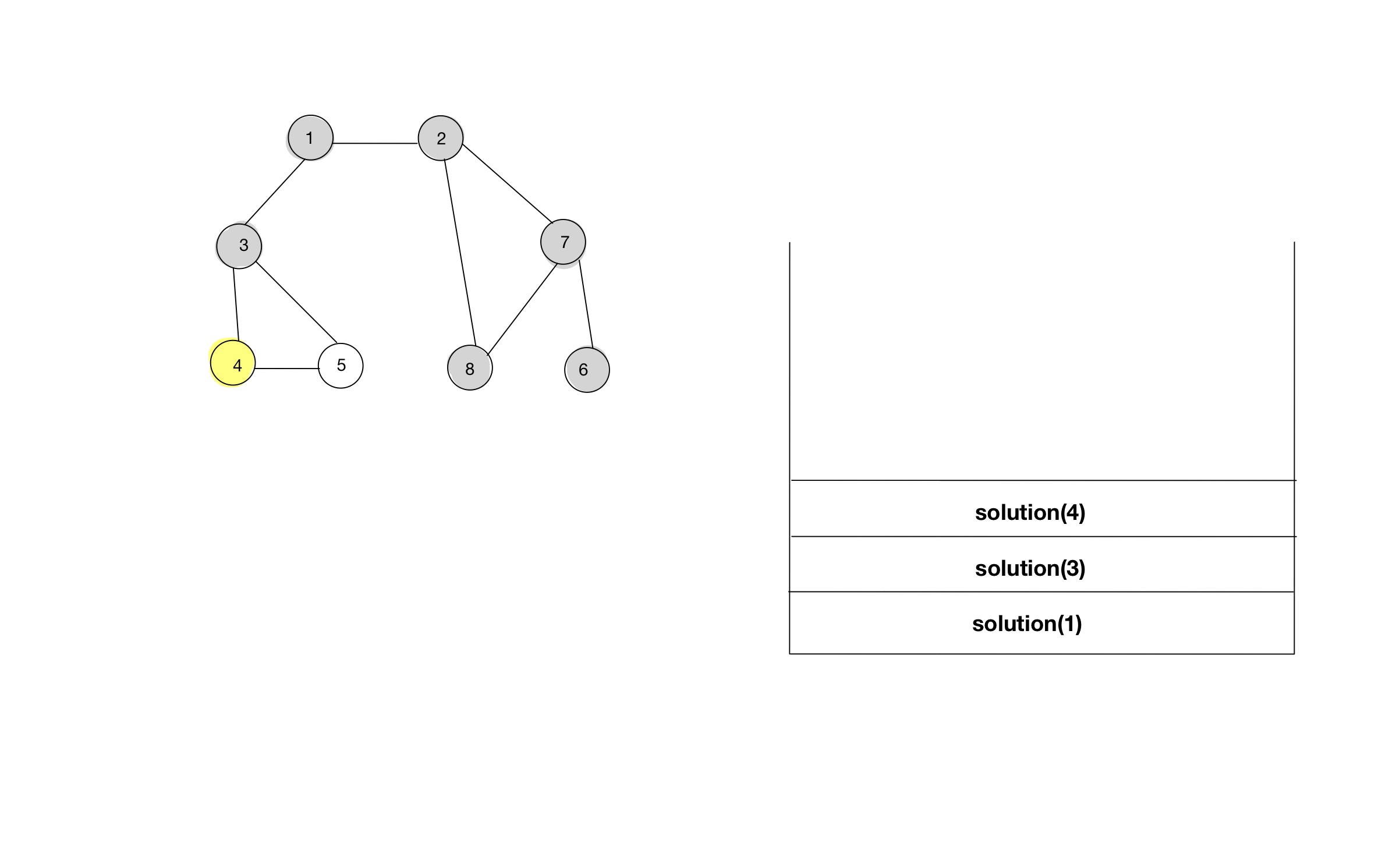
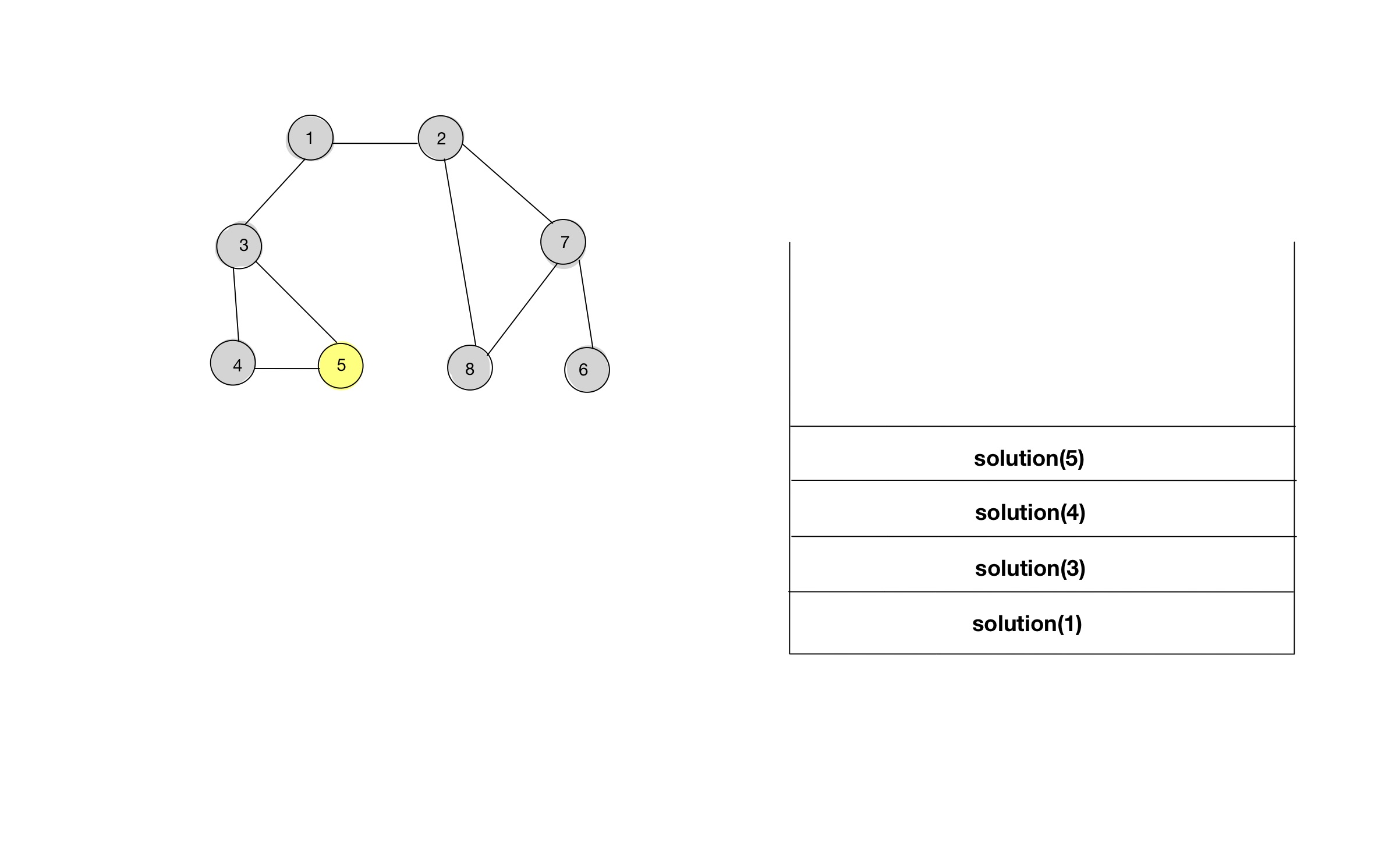
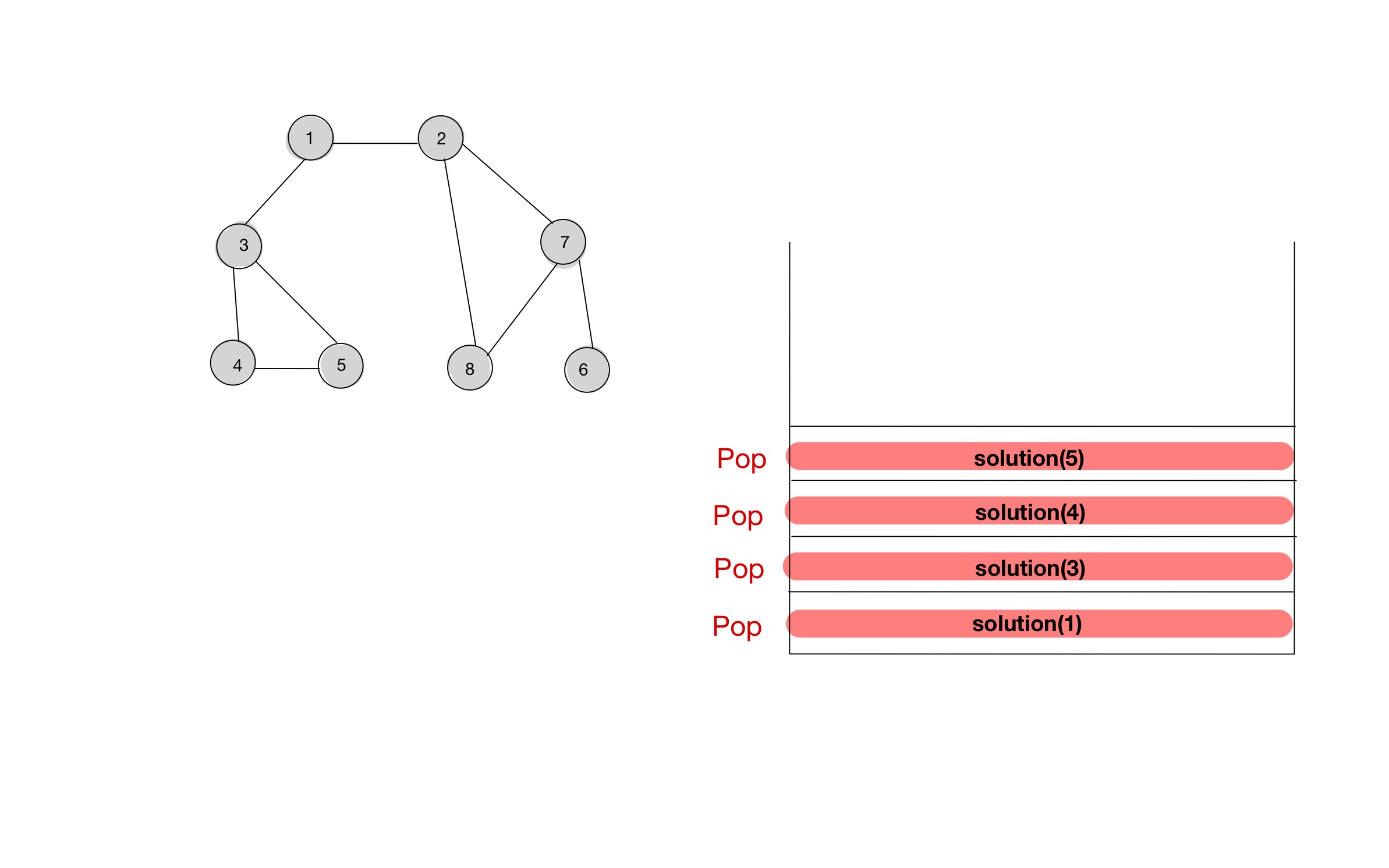
소스코드 - 인접행렬
DFS 알고리즘
public class DFS_MatrixGraph {
private int numberOfNode;
private boolean[][] graph; //0행과 0열은 건너뛴다. (인접하다면 true)
private boolean[] visitedNode;
private DFS_MatrixGraph() {
}
public DFS_MatrixGraph(int numberOfNode, boolean[][] graph) {
this.numberOfNode = numberOfNode;
this.graph = graph; //0행은 비어있어야 한다.
visitedNode = new boolean[numberOfNode + 1];
}
public void solution(int indexOfNowNode) {
//노드 방문
visitedNode[indexOfNowNode] = true;
//방문한 노드 출력
System.out.print(indexOfNowNode + " ");
for (int i = 1; i <= numberOfNode; i++) {
//현재 노드(indexOfNow)와 인접한(연결된) 노드라면
if (graph[indexOfNowNode][i]) {
//방문하지 않은 노드라면
if (!visitedNode[i]) {
solution(i);
}
}
}//for문 종료
}
}
DFS 알고리즘 실행
public class Main {
/**
* DFS 실행 메서드
*/
public static void execute() {
int numberOfNode = 8;
//graph (true면 인접)
boolean[][] graph = new boolean[][] {
{false, false, false, false, false, false, false, false, false},
{false, false, true, true, false, false, false, false, false},
{false, true, false, false, false, false, false, true, true},
{false, true, false, false, true, true, false, false, false},
{false, false, false, true, false, true, false, false, false},
{false, false, false, true, true, false, false, false, false},
{false, false, false, false, false, false, false, true, false},
{false, false, true, false, false, false, true, false, true},
{false, false, true, false, false, false, false, true, false}
};
DFS_MatrixGraph dfs = new DFS_MatrixGraph(numberOfNode, graph);
dfs.solution(1);
}
}
본 소스코드의
graph는 위 그림 예시에서 사용한 그래프와 동일한 것이다.
- 모든 첫번째 행과, 모든 첫번째 열은 false로 처리했다. (노드가 1부터 시작하므로)
graph[A][A]와 같이 자기자신을 의미하는 index의 경우, false로 처리했다.- true: 해당 노드끼리 인접한다.
- false: 해당 노드끼리 인접하지 않는다.
- 예시
graph[4][5] = true: ‘노드4’와 ‘노드5’가 인접한다.graph[7][1] = false: ‘노드7’과 ‘노드1’은 인접하지 않는다.
출력결과
1 2 7 6 8 3 4 5
소스코드 흐름
인접리스트 방식과 동일하다.
Tip
- 그래프 탐색 문제가 인접 이 핵심 내용이라면, 주로 DFS를 사용한다.
- 나동빈, 『이것이 코딩 테스트다』
