분할 정복 : 합병 정렬

개요

특징

입력
- 2개의 부분 문제로 분할
- 부분 문제 크기: 1/2로 감소

단점

입력을 위한 메모리 공간 외의 추가로 입력과 같은 크기의 공간 필요

하지만 큰 의미는 없다.

정복방법

n개의 숫자들을 n/2개씩 2개의 부분문제로 분할
각각의 부분문제를 재귀적으로 합병정렬
2개의 정렬된 부분을 합병

합병 과정 == 정복

알고리즘

의사코드

흐름 순서

3번째 줄이 끝난 후, 4번째 줄 시작

흐름순서

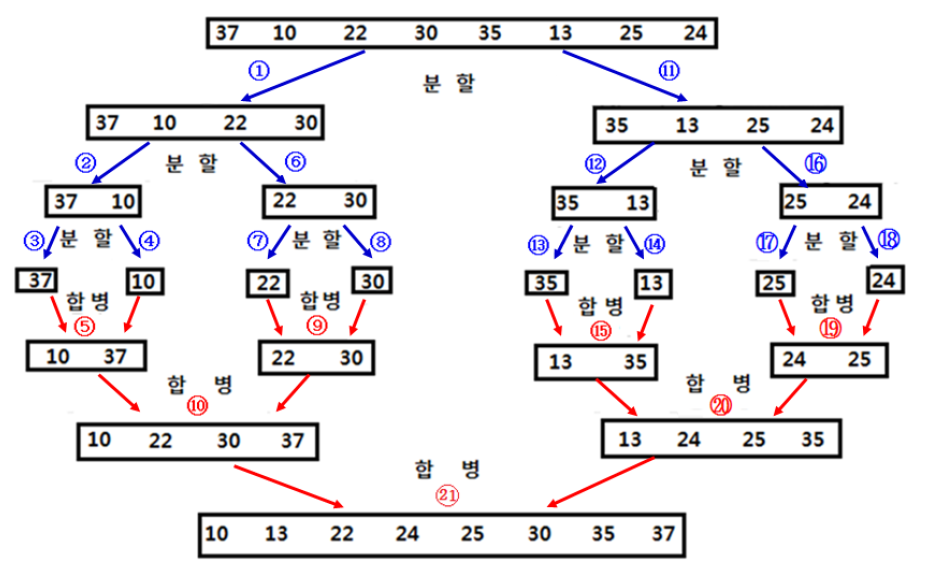
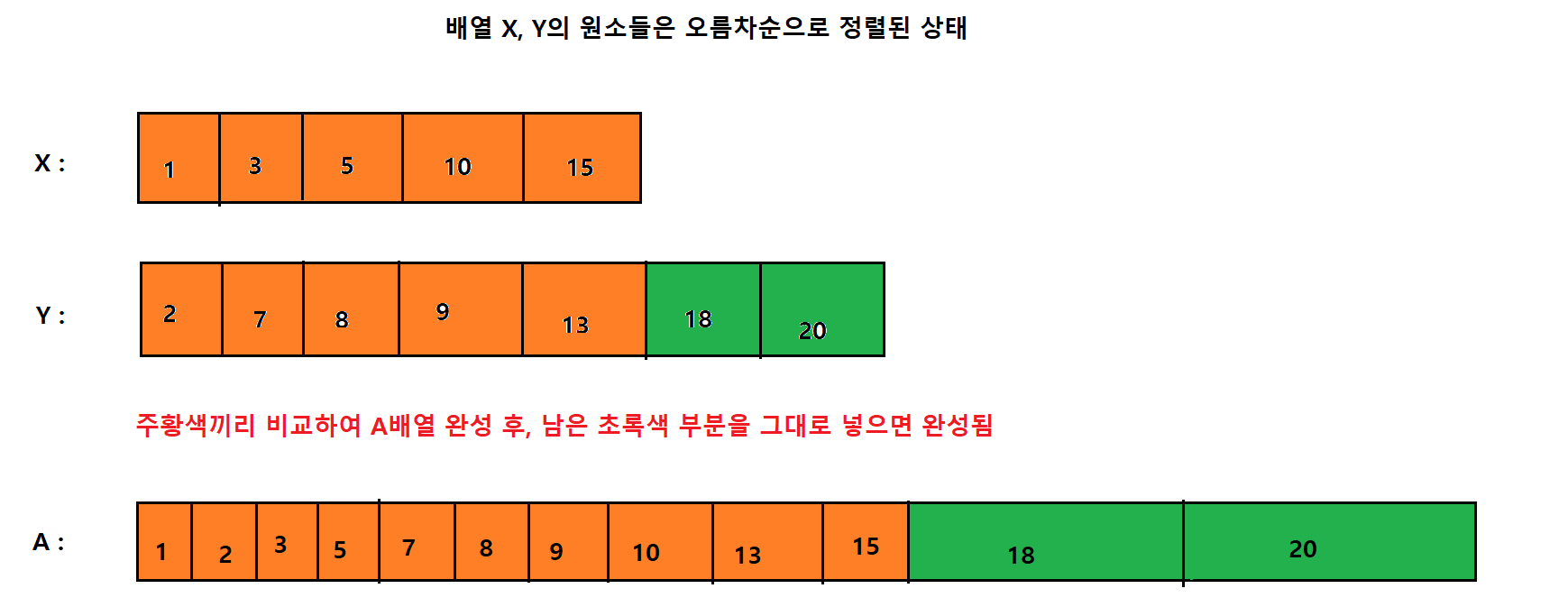
합병 방법

흐름순서1

흐름순서2

시간 복잡도

합병 수행 시간
- 배열 A[n], B[m] 일때, 최대 비교 횟수 = n+m-1
- n+m 개의 공간을 채우기 위한 최대 비교 횟수 (worst case)
- 최악의 경우:
  (m+n) 길이의 배열을 채울때, (m+n-1)번 비교해야함
n + m -1 : 맨 마지막건 비교X
(하지만, 큰 의미X ⇒ 무시가능)

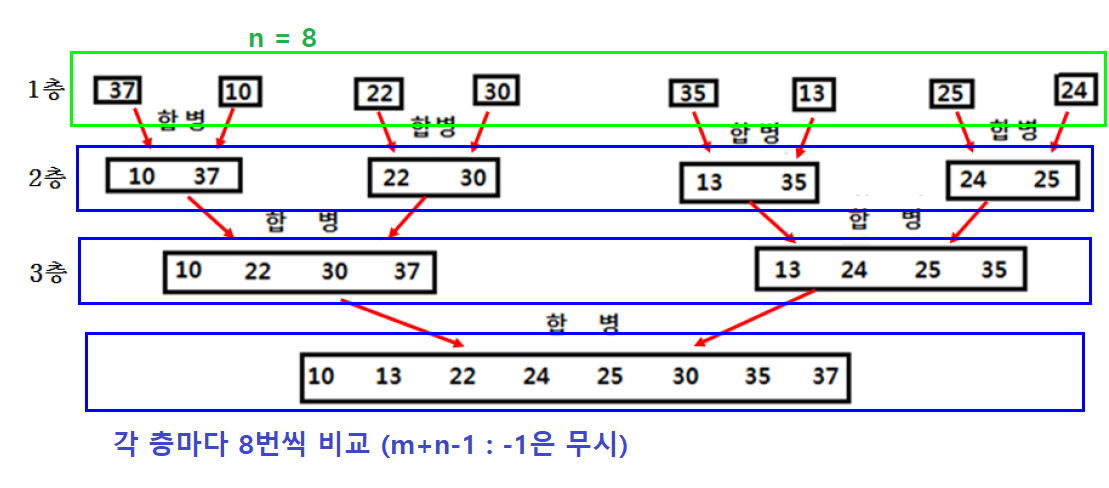
시간복잡도

각 층의 비교횟수 : O(n)

따라서, n을 1/2로 계속 나누어 총 k번 분할하여 계산하므로
층의 개수: $k$
$k$ : $n=2^k$ 이므로 $k=log_2n$
결과적으로 합병 정렬의 시간복잡도
⇒ 층수 * 각층계산시간 =
$log_{2}n * O(n) = O(nlog_{2}n) = O(nlogn)$