logo img Dev Blog

[데이터구조] 이진탐색트리

July 16, 2021

이진 탐색 트리

개요

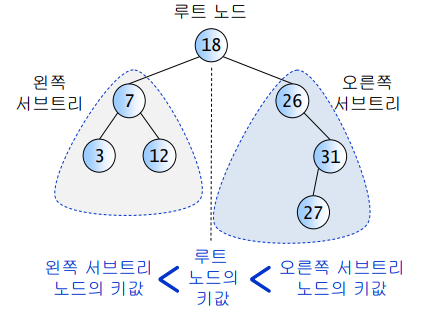
이진 탐색 트리 정의

  • 각 노드의 값으로 key값을 갖는다. ⇒ 따라서, 중복이 안된다.
  • 왼쪽서브트리
    • 루트노드보다 작은 값
  • 오른쪽서브트리
    • 루트노드보다 큰 값

이진 탐색 트리를 중위순회하면 오름차순으로 정렬된 값을 구할 수 있음 ⇒ 이진 탐색을 수행하기 위해, 선행되어야함

이진탐색트리 구조



이진 탐색 트리 연산 개요

연산 개요

  • 기본적인 연산은 이진 트리와 동일하다.


  • 연산 종류
    • 삽입
    • 삭제
    • 탐색


  • 연산 조건
    • 이진탐색트리의 조건을 유지하면서 처리되야함
    • 왼쪽 서브 트리 ⇒ 루트노드보다 작은 값
    • 오른쪽 서브 트리 ⇒ 루트노드보다 큰 값
  • 연산 특징
    • 삽입이나 삭제 연산시, 무조건 탐색이 선행되어야함
    • 왜냐하면 삽입시, 삽입할 값과 중복되는 노드값이 존재하는지 확인해야함 (키값 중복 방지)
    • 또한 삭제시, 삭제할 노드 탐색



이진 탐색 트리 연산: 탐색 연산

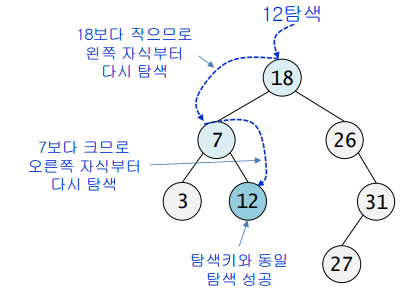
탐색 연산 개요

  • 탐색은 항상 루트 노드에서 시작
  • 키 값(찾으려는 값)이 루트보다 작으면 ⇒ 왼쪽 자식을 기준으로 다시 탐색
  • 키 값(찾으려는 값)이 루트보다 크면 ⇒ 오른쪽 자식을 기준으로 다시 탐색
  • 반복


탐색 알고리즘

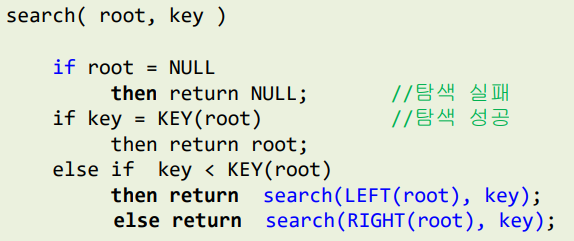
탐색알고리즘 1

탐색알고리즘 2


탐색 함수 구현 - 순환적 탐색 함수

TNode* search( TNode *n, int key ) {
	if(n==NULL) {
		return NULL;
	} else if(key == n->data) {
		return n;
	} else if(key < n->data) {
		return search(n->left, key);
	} else {
		return search(n->right, key);
	}
}


탐색 함수 구현 - 반복적 탐색 함수

TNode* search_iter( TNode *n, int key ) {
	while( n!=NULL ) {
		if( key == n->data ) {
			return n;
		} else if( key < n->data ) {
			n = node->left;
		} else {
			n = node->right;
		}
	return NULL; //탐색실패
}



이진 탐색 트리 연산: 삽입 연산

삽입 연산 개요

  • 노드를 삽입하기 전에 먼저 탐색을 수행
  • 중복노드 삽입 불가
  • 탐색에 실패한 위치 == 새로운 노드를 삽입하는 위치

삽입연산


삽입 알고리즘

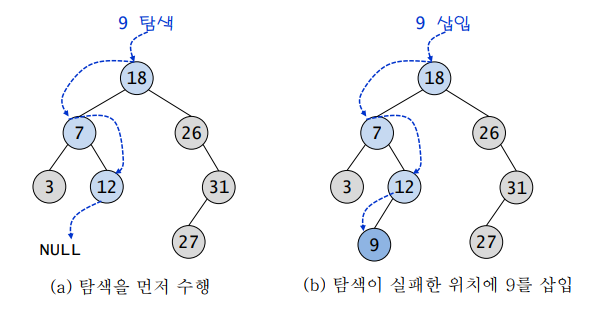
삽입연산 알고리즘


삽입 함수 구현

int insert( TNode *r, TNode *n ) { // r: 루트노드, n: 삽입할 노드

	if(n->data == r->data) { //중복되어 삽입 실패
		return 0;
	}
	else if(n->data < r->data) {
		if(r->left == NULL) { //삽입할 자리 찾음
			r->left = n;
		} else {              //삽입할 자리 못찾음
			insert(r->left, n);
		}
	}
	else {
		if(r->right == NULL) { //삽입할 자리 찾음
			r->right = n;
		} else {               //삽입할 자리 못찾음
			insert(r->right, n);
		}
	}
	return 1; //삽입성공

}



이진 탐색 트리 연산: 삭제 연산

삭제 연산 개요

  • 노드 삭제의 3가지 경우가 존재

    1. 단말 노드를 삭제할 경우
    2. 자식이 하나인 노드를 삭제하려는 경우
      (삭제하려는 노드가 오른쪽이나 왼쪽 서브 트리만 가지고 있을때)
    3. 자식이 둘인 노드를 삭제하려는 경우
      (삭제하려는 노드가 오른쪽과 왼쪽 서브 트리 모두 가지고 있을때)


단말 노드 삭제시

  • 단말 노드의 부모 노드를 찾아서 연결을 끊으면 됨

삭제연산


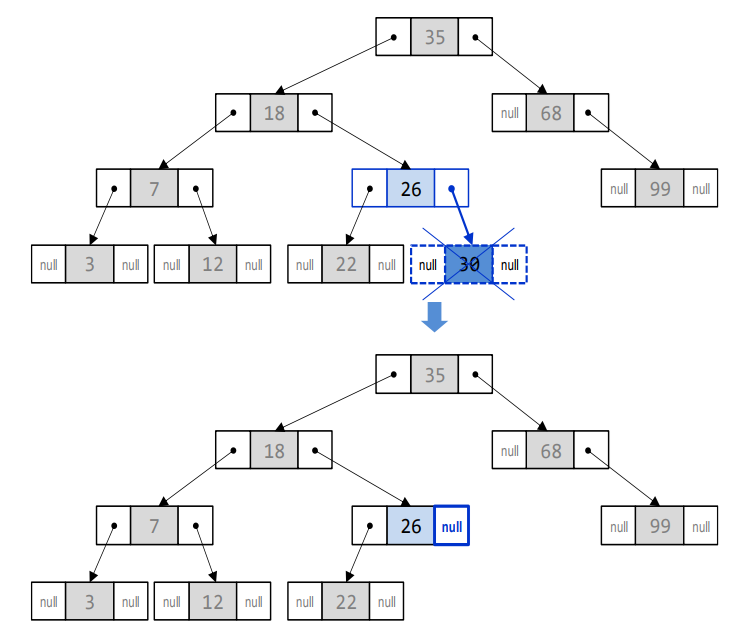
자식이 하나인 노드 삭제시

  • 목표 노드 삭제 후, 해당 노드의 서브 트리는 부모 노드에 붙여줌

  • 삭제시 고려사항

    • 삭제할 노드의 자식이 왼쪽or오른쪽 자식일 수 있다.
    • 삭제할 노드가 부모의 왼쪽or오른쪽 자식일 수도 있다.

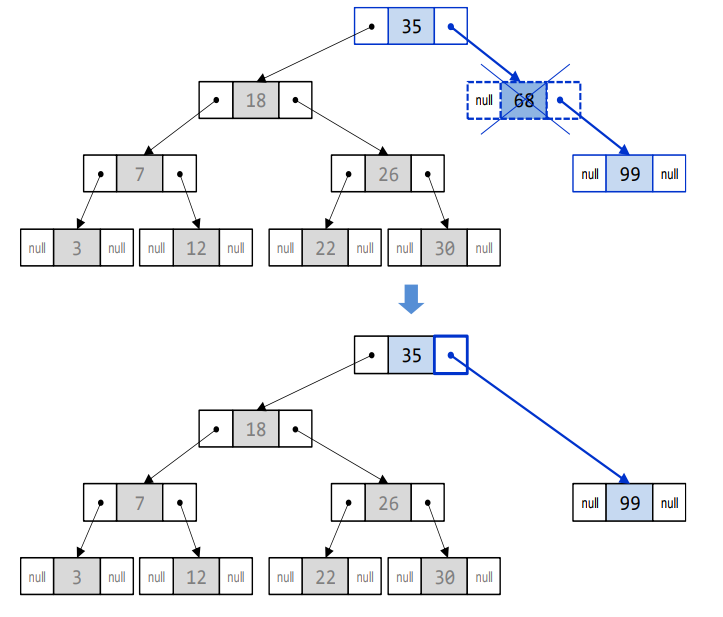
자식이 하나인 노드삭제


두 개의 자식을 가진 노드 삭제시

  • 가장 비슷한 값을 가진 노드를 삭제 노드 위치로 가져옴


  • 후계노드란?
    • 삭제되는 노드와 값이 가장 비슷한 노드
    • 삭제할 노드의 값에 후계노드의 값이 덮어씌워짐
  • 후계노드 선정방법
    • 삭제할 노드의 왼쪽 서브 트리에서 가장 오른쪽 아래노드 (제일 큰 값)
      (Leaf노드가 아닐수있다.)
    • 삭제할 노드의 오른쪽 서브 트리에서 가장 왼쪽 아래노드 (제일 작은 값)
      (Leaf노드가 아닐수있다.)

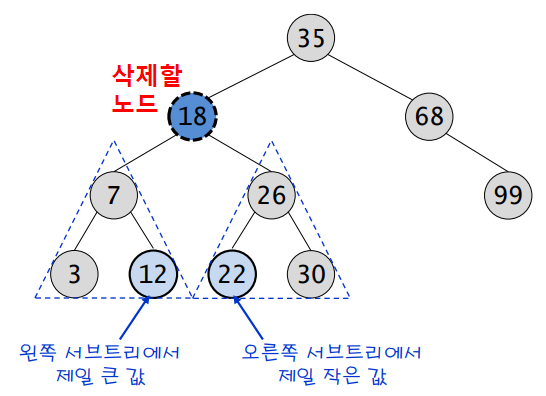
후계노드 선정

총 2개의 후계 노드가 존재함


  • 주의점

    • 후계 노드로 선택된 노드가 또다른 자식 노드를 가질 수도 있음

주의점1

주의점2


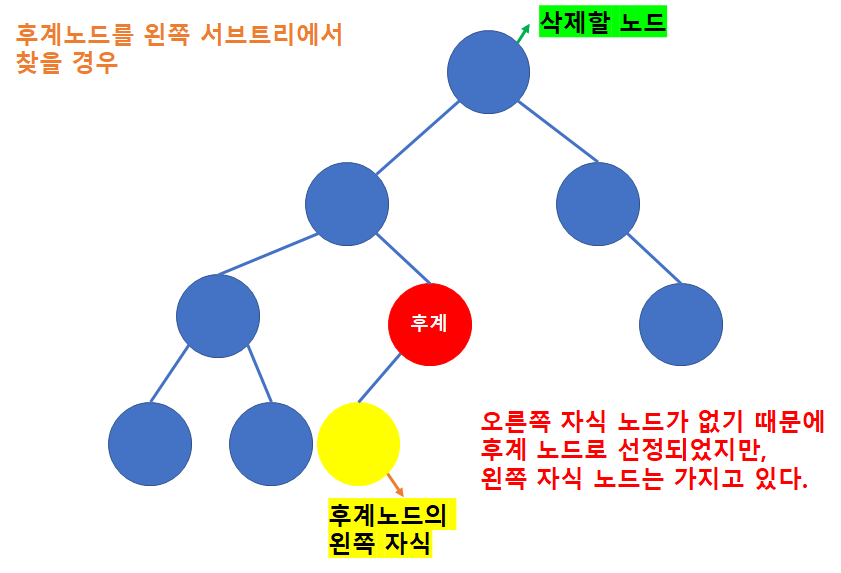
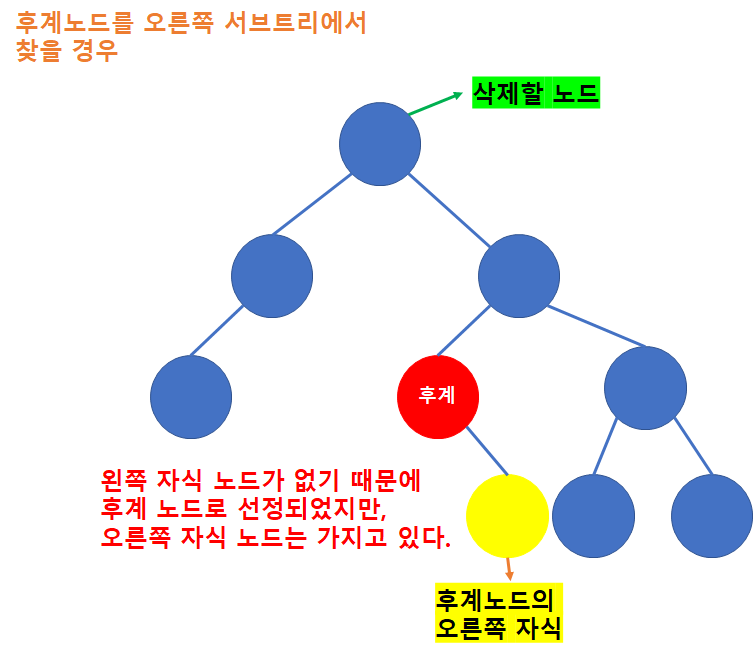
  • 후계자 노드 찾기

    • 삭제되는 노드의 오른쪽 서브트리에서 찾기
      • 오른쪽 서브트리에서 왼쪽 자식 링크를 타고 NULL을 만날 때까지 계속 진행
    • 삭제되는 노드의 왼쪽 서브트리에서 찾기
      • 왼쪽 서브트리에서 오른쪽 자식 링크를 타고 NULL을 만날 때까지 계속 진행

  • 원리

    1. 삭제할 노드를 대신할 적절한 후계자 노드를 찾는다. (총 2개의 후계자 노드가 존재함)
    2. 그 중 하나의 후계자 노드를 선택 (아무것이나 선택 가능)
    3. 선택된 후계자 노드의 값(key값)을 삭제할 노드에 덮어씌움
    4. 선택된 후계자 노드를 삭제

이진탐색트리 원리

만약 후계자 노드를 오른쪽 서브트리에서 찾았다면, 해당 후계자 노드의 오른쪽 자식이 존재할 수도 있으므로, 후계자 노드의 오른쪽 링크를 “후계자 노드의 부모노드”의 왼쪽 링크로 복사해야한다.


이진탐색트리 삭제 함수 구현

void delete(TNode *parent, TNode *node) { // parent: 삭제할 노드의 부모노드, node: 삭제할 노드 
	TNode *child, *succ, *succp;
	//child: case2에서 사용될 변수, "삭제할 노드의 왼쪽or오른쪽 자식노드"
	//succ: case3에서 사용될 변수, "후계 노드"
	//succp: case3에서 사용될 변수, "후계 노드의 부모노드" 
	
	
	//case 1 : 삭제할 노드가 잎새노드일 때
	if( (node->left == NULL) && (node->right == NULL) ) {
		if( parent == NULL ) { // 탐색 실패시 
			root = NULL;
		} else { //탐색 성공시 
			if(parent->left == node) {
				parent->left = NULL; // 노드 삭제 
			} else {
				parent->right = NULL; // 노드 삭제 
			}
		}
	}
	
	//case 2 : 삭제할 노드가 1개의 서브 트리를 가지고 있을 때 
	else if( (node->left == NULL) || (node->right == NULL) ) {
		child = (node->left != NULL) ? node->left : node->right; //삭제할 노드의 왼쪽 노드 or 오른쪽 노드를 child에 저장 
		if(node == root) { //삭제할 노드가 전체 트리의 루트노드 일때
			root = child;
		} else {
			
			if(parent->left == node) { //삭제할 노드가 parent의 왼쪽 노드라면 
				parent->left = child; //부모노드의 왼쪽 서브트리로서 child를 붙임 
			} else {                  //삭제할 노드가 parent의 오른쪽 노드라면
				parent->right = child;//부모노드의 오른쪽 서브트리로서 child를 붙임
			}
			
		}
	}
	
	//case 3 : 삭제할 노드가 2개의 서브 트리를 가지고 있을 때 
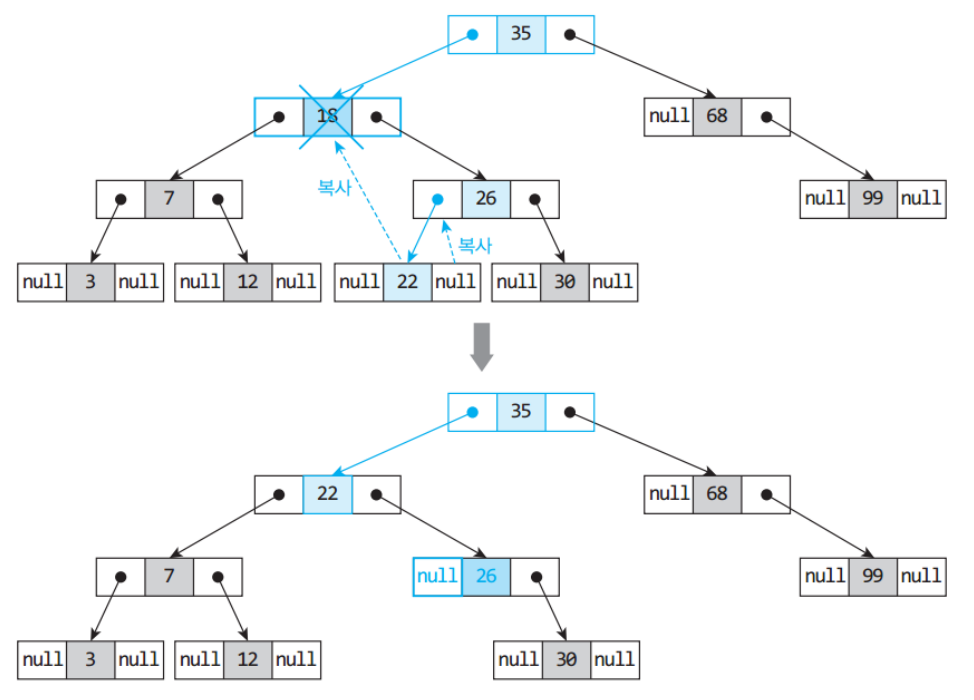
	else {
		succp = node; //후계 노드의 부모노드 초기화 
		succ = node->right; //삭제할 노드의 오른쪽 서브트리에서 후계노드를 찾겠다. 
		
		while(succ->left != NULL) { //삭제할 노드의 오른쪽 서브트리에서 왼쪽 자식노드를 반복해서 찾아들어감
			succp = succ;
			succ = succ->left;
		}
		
		//후계 노드를 찾기 위해 왼쪽 자식노드를 파고 들어감
		//후계 노드가 자식노드를 가지고 있을 수 있으므로, 해당 부분 처리 
		if(succp->left == succ) {
			succp->left = succ->right;
		} else {
			succp->right = succ->right;
		}
		
		node->data = succ->data; //삭제할 노드의 값(key)을 "후계 노드의 값(key)로 변경" 
		node = succ; 
	}
	
	free(node); //삭제할 노드 제거 
}



이진 탐색 전체 프로그램 구현

인터페이스 함수

  • 인터페이스 함수
    • 함수를 보다 편리하게 사용할 수 있게 사용자에게 안내해주는 함수
//인터페이스 함수: search() 함수를 위한 함수
void search_BST(int key) {
	TNode *n = search(root, key);
	if(n != NULL) {
		printf("[탐색 연산] : 성공 [%d] = 0x%x\n", n->data, n);
	} else {
		printf("[탐색 연산] : 실패: No %d!\n", key);
	}
}

//인터페이스 함수: insert() 함수를 위한 함수
void insert_BST(int key) {
	TNode *n = create_tree(key, NULL, NULL);
	if(is_empty_tree()) {
		root = n;
	} else if(insert(root, n)==0) {
		free(n);
	}
}

//삭제연산 인터페이스 함수
void delete_BST(int key) {
	TNode *parent = NULL;
	TNode *node = root;
	
	if( node == NULL ) {
		return;
	}
	
	while( (node != NULL) && (node->data != key) ) {
		parent = node;
		node = (key < node->data) ? node->left : node->right;
	}
	if(node == NULL) {
		printf("Error: key is not in the tree!\n");
	} else {
		delete(parent, node);
	}
}


전체 프로그램

#include <stdio.h>
#include <stdlib.h>

typedef int TElement;
typedef struct BinTrNode {
	TElement data;
	struct BinTrNode *left;
	struct BinTrNode *right;
} TNode;

TNode *root = NULL;

void init_tree() {
	root = NULL;
}

int is_empty_tree() {
	return root==NULL;
}

TNode* get_root() {
	return root;
}

TNode* create_tree( TElement val, TNode *left, TNode *right ) {
	TNode *n = (TNode*)malloc(sizeof(TNode));
	n->data = val;
	n->left = left;
	n->right = right;
	return n;
}

//--------------------------------순회---------------------------------

//전위순회 
void preorder(TNode *n) {
	if(n!=NULL) {
		printf("[%c] ", n->data);
		preorder(n->left);
		preorder(n->right);
	}
} 

//중위순회
void inorder(TNode *n) {
	if(n!=NULL) {
		preorder(n->left);
		printf("[%c] ", n->data);
		preorder(n->right);
	}
}

//후위순회
void postorder(TNode *n) {
	if(n!=NULL) {
		preorder(n->left);
		preorder(n->right);
		printf("[%c] ", n->data);
	}
}

//--------------------------------이진탐색---------------------------------

//탐색 연산 
TNode* search( TNode *n, int key ) {
	if(n==NULL) {
		return NULL;
	} else if(key == n->data) {
		return n;
	} else if(key < n->data) {
		return search(n->left, key);
	} else {
		return search(n->right, key);
	}
}

//탐색 연산 인터페이스 함수
void search_BST(int key) {
	TNode *n = search(root, key);
	if(n != NULL) {
		printf("[탐색 연산] : 성공 [%d] = 0x%x\n", n->data, n);
	} else {
		printf("[탐색 연산] : 실패: No %d!\n", key);
	}
}

//삽입연산
int insert( TNode *r, TNode *n ) { // r: 루트노드, n: 삽입할 노드

	if(n->data == r->data) { //중복되어 삽입 실패
		return 0;
	}
	else if(n->data < r->data) {
		if(r->left == NULL) { //삽입할 자리 찾음
			r->left = n;
		} else {              //삽입할 자리 못찾음
			insert(r->left, n);
		}
	}
	else {
		if(r->right == NULL) { //삽입할 자리 찾음
			r->right = n;
		} else {               //삽입할 자리 못찾음
			insert(r->right, n);
		}
	}
	return 1; //삽입성공

}

//삽입연산 인터페이스 함수 
void insert_BST(int key) {
	TNode *n = create_tree(key, NULL, NULL);
	if(is_empty_tree()) {
		root = n;
	} else if(insert(root, n)==0) {
		free(n);
	}
}

//삭제연산 
void delete (TNode *parent, TNode *node) { // parent: 삭제할 노드의 부모노드, node: 삭제할 노드 
	TNode *child, *succ, *succp;
	//child: case2에서 사용될 변수, "삭제할 노드의 왼쪽or오른쪽 자식노드"
	//succ: case3에서 사용될 변수, "후계 노드"
	//succp: case3에서 사용될 변수, "후계 노드의 부모노드" 
	
	
	//case 1 : 삭제할 노드가 잎새노드일 때
	if( (node->left == NULL) && (node->right == NULL) ) {
		if( parent == NULL ) { // 탐색 실패시 
			root = NULL;
		} else { //탐색 성공시 
			if(parent->left == node) {
				parent->left = NULL; // 노드 삭제 
			} else {
				parent->right = NULL; // 노드 삭제 
			}
		}
	}
	
	//case 2 : 삭제할 노드가 1개의 서브 트리를 가지고 있을 때 
	else if( (node->left == NULL) || (node->right == NULL) ) {
		child = (node->left != NULL) ? node->left : node->right; //삭제할 노드의 왼쪽 노드 or 오른쪽 노드를 child에 저장 
		if(node == root) { //삭제할 노드가 전체 트리의 루트노드 일때
			root = child;
		} else {
			
			if(parent->left == node) { //삭제할 노드가 parent의 왼쪽 노드라면 
				parent->left = child; //부모노드의 왼쪽 서브트리로서 child를 붙임 
			} else {                  //삭제할 노드가 parent의 오른쪽 노드라면
				parent->right = child;//부모노드의 오른쪽 서브트리로서 child를 붙임
			}
			
		}
	}
	
	//case 3 : 삭제할 노드가 2개의 서브 트리를 가지고 있을 때 
	else {
		succp = node; //후계 노드의 부모노드 초기화 
		succ = node->right; //삭제할 노드의 오른쪽 서브트리에서 후계노드를 찾겠다. 
		
		while(succ->left != NULL) { //삭제할 노드의 오른쪽 서브트리에서 왼쪽 자식노드를 반복해서 찾아들어감
			succp = succ;
			succ = succ->left;
		}
		
		//후계 노드를 찾기 위해 왼쪽 자식노드를 파고 들어감
		//후계 노드가 자식노드를 가지고 있을 수 있으므로, 해당 부분 처리 
		if(succp->left == succ) {
			succp->left = succ->right;
		} else {
			succp->right = succ->right;
		}
		
		node->data = succ->data; //삭제할 노드의 값(key)을 "후계 노드의 값(key)로 변경" 
		node = succ; 
	}
	
	free(node); //삭제할 노드 제거 
}

//삭제연산 인터페이스 함수
void delete_BST(int key) {
	TNode *parent = NULL;
	TNode *node = root;
	
	if( node == NULL ) {
		return;
	}
	
	while( (node != NULL) && (node->data != key) ) {
		parent = node;
		node = (key < node->data) ? node->left : node->right;
	}
	if(node == NULL) {
		printf("Error: key is not in the tree!\n");
	} else {
		delete(parent, node);
	}
}

void main() {
	
	init_tree();
	printf("[삽입 연산] : 35 18 7 26 12 3 68 22 30 99");
	init_tree();
	insert_BST(35); insert_BST(18);
	insert_BST(7); insert_BST(26);
	insert_BST(12); insert_BST(3);
	insert_BST(68); insert_BST(22);
	insert_BST(30); insert_BST(99);
	
	// 트리 정보 출력
	printf("\n In-Order : "); inorder(root);
	printf("\n Pre-Order : "); preorder(root);
	printf("\n Post-Order : "); postorder(root);
	
	//트리 정렬
	
	
	// 탐색 연산 테스트
	search_BST(26);
	search_BST(25);

//	// 삭제 연산 테스트
//	delete_BST(3);
//	delete_BST(68);
//	delete_BST(18);
//	delete_BST(35);

}



이진탐색트리 성능

최선의 경우

  • 이진 트리가 균형적으로 생성되어 있는 경우

  • O(logn)

최악의 경우

  • 경사 이진 트리일 경우

  • O(n)




  • 성결대학교 컴퓨터 공학과 박미옥 교수님 (2021)
  • 최영규, 『두근두근 자료구조』
본 게시글은 위 강의 및 교재를 기반으로 정리한 글입니다.