순열과 순열 알고리즘
개요
순열이란?
= n개의 원소 중, 순서를 고려하여 r개를 선택하는 경우의 수
순열 알고리즘 구현 방식
- 재귀함수와
visited배열을 활용하여, 순열을 구한다. - DFS, 백트래킹 기법을 사용한다.
예시 코드
문제
구하기
- 주어진 배열:
{1, 2, 3}
소스코드
public class 순열 {
static int[] numbers = {1, 2, 3};
static boolean[] visited = new boolean[3];
static int[] result = new int[3];
static int n = 3;
static int r = 2;
public static void permutation(int depth) {
if (depth == r) { //r개의 원소를 모두 골랐다면 탈출
print();
}
for (int i = 0; i < n; i++) {
if (visited[i]) continue; //i번째 원소가 이미 선택되어 있다면, 뽑는것을 생략한다.
visited[i] = true; //i번째 원소를 뽑는다.
result[depth] = numbers[i]; //뽑은 순서를 기억하기 위해, result 배열에 depth를 인덱스로 삼아 저장한다.
permutation(depth+1); //재귀호출을 하여, 나머지를 뽑는다.
//위 재귀호출을 통해, 나머지를 모두 뽑아 결과를 확인했으므로
//i번째 원소를 뽑지 않고, 다음 원소를 고려하도록 false로 설정한다.
visited[i] = false;
}
}
/**
* 출력 메서드
*/
private static void print() {
for (int i = 0; i < r; i++) {
System.out.print(result[i] + " ");
}
System.out.println();
}
}
재귀 흐름
1.
2.
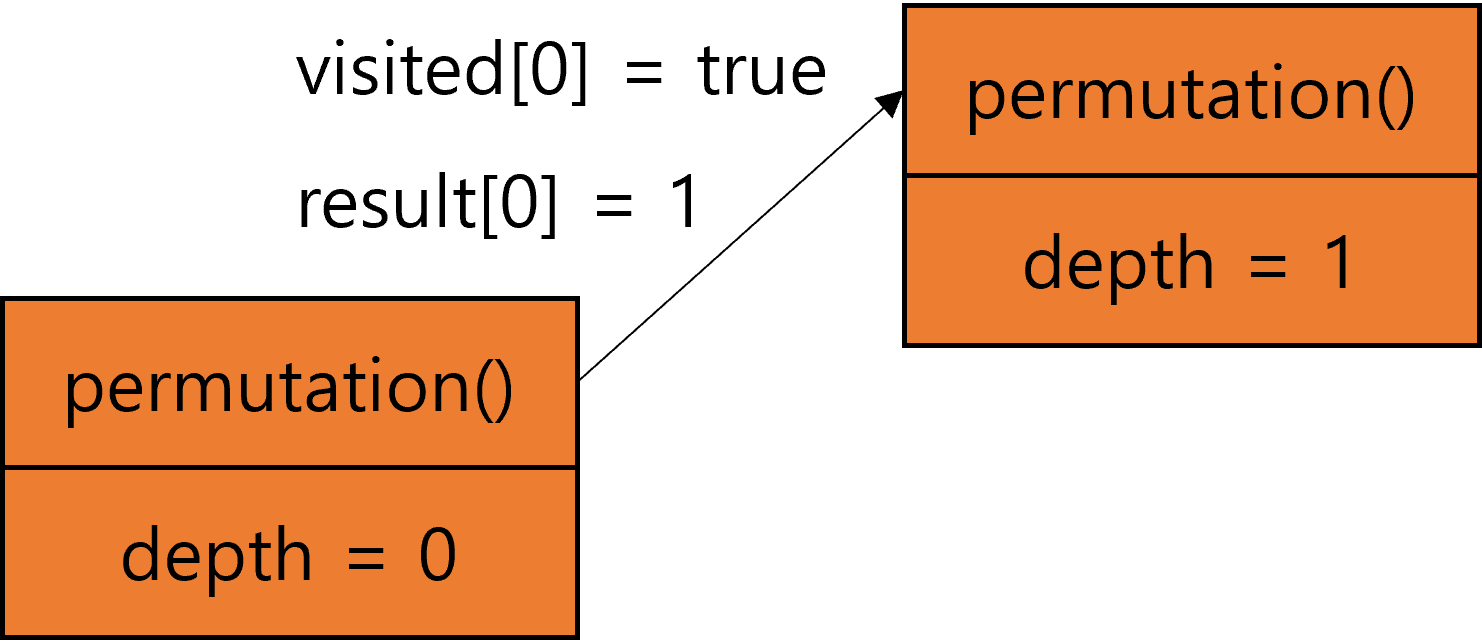
3.
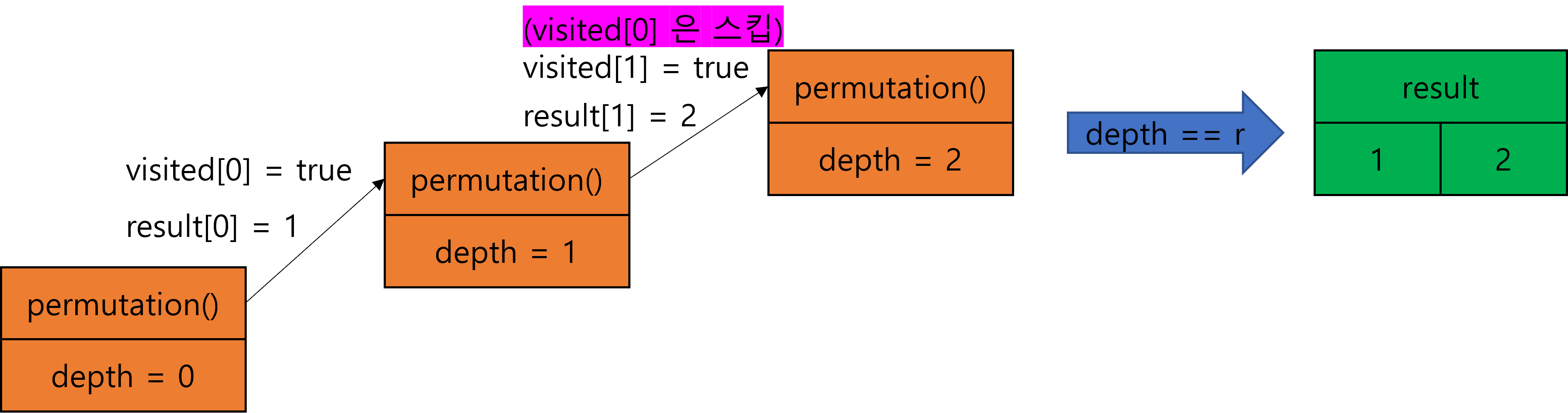
4.
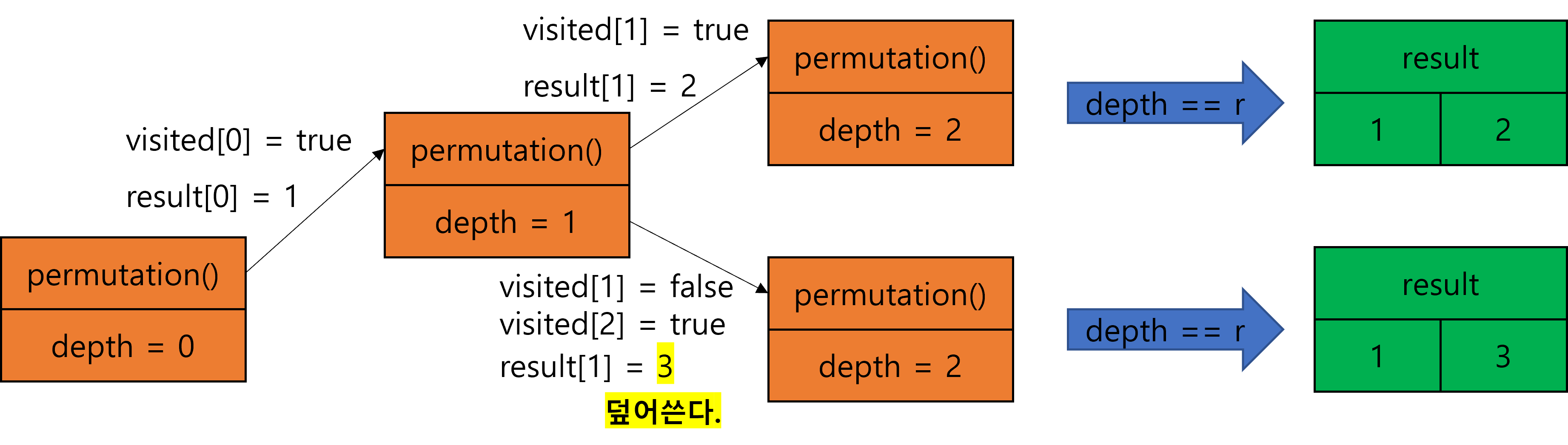
5.
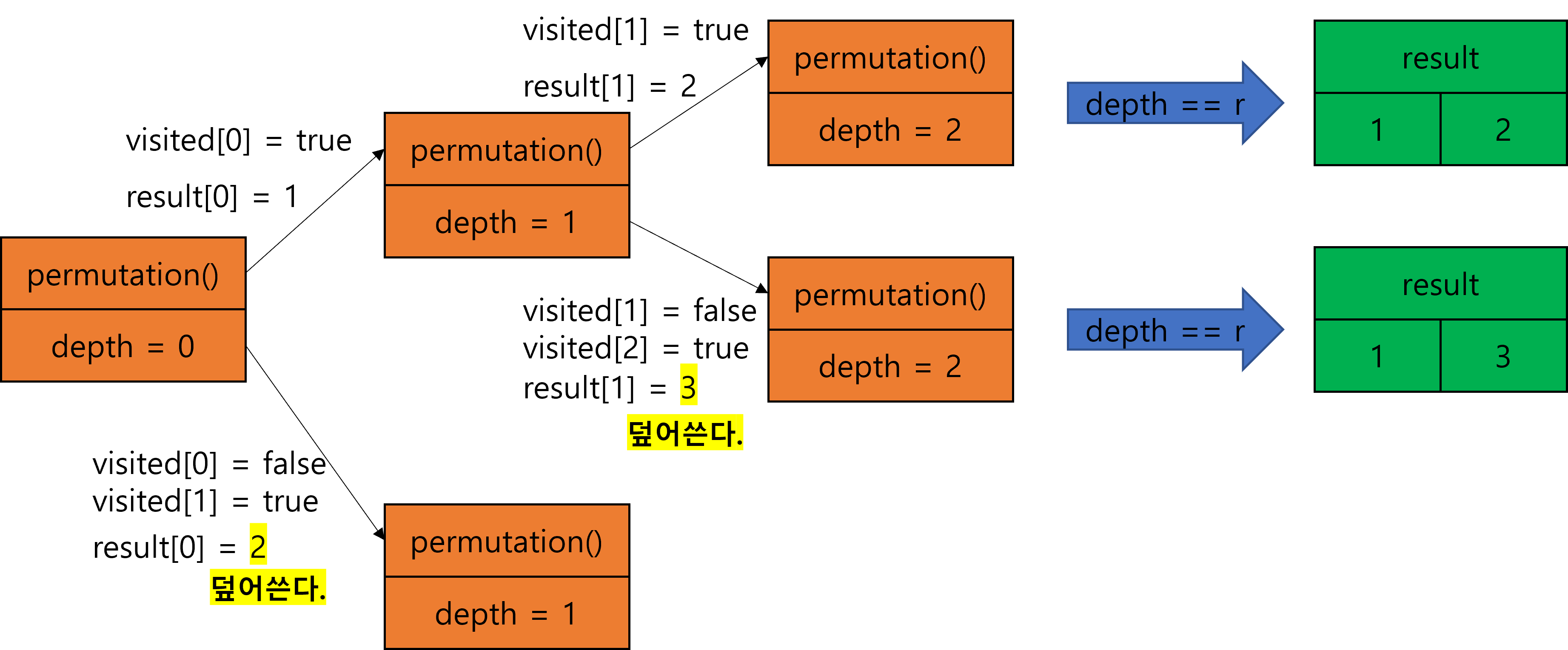
6.
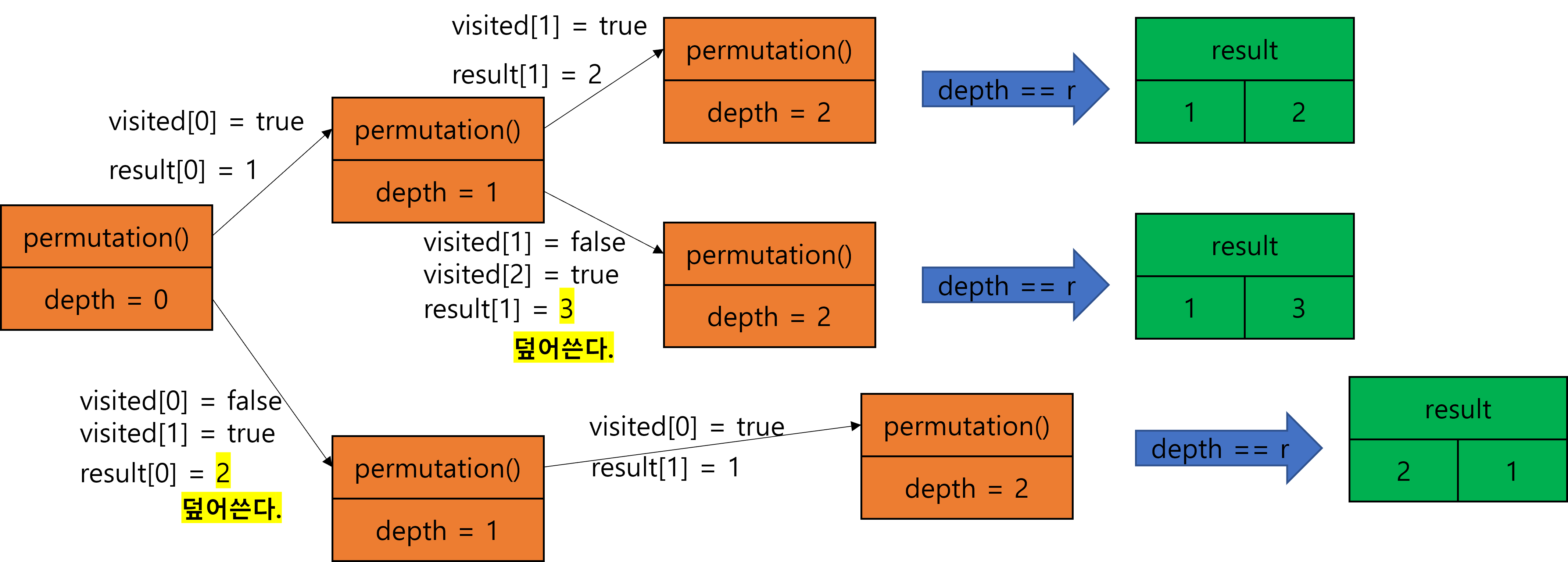
7.
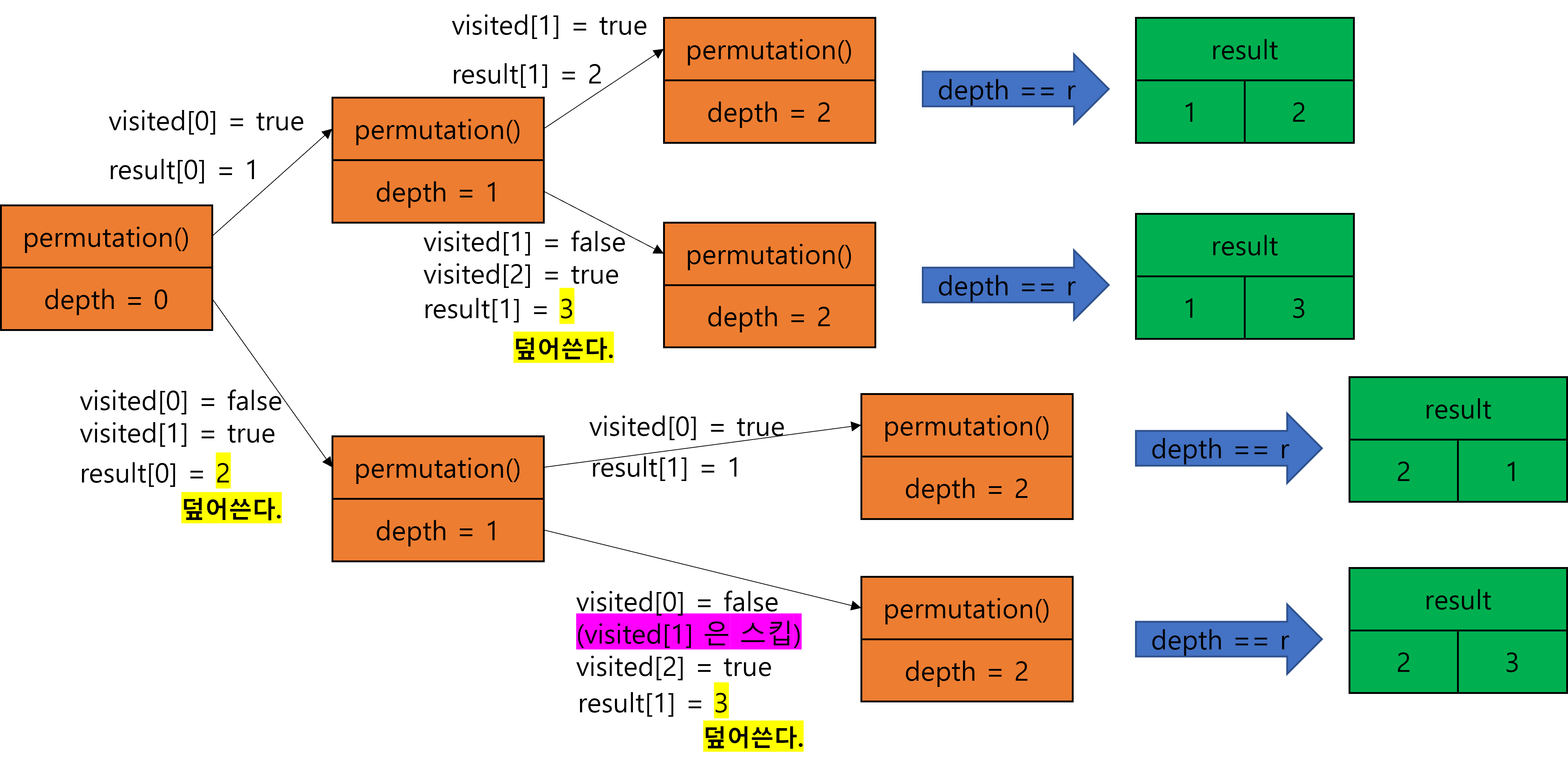
이하 생략
중복 가능한 순열 구하기
코드
public class 중복_순열 {
static int[] numbers = new int[] {1, 2, 3};
static int r = 3;
static int[] result = new int[3];
//3개의 원소 중, 순서를 고려하여 중복해서 3개를 뽑기
public static void permutation(int depth, int r) { //n은 필요없다.
if (r == 0) { //3개를 모두 뽑았다면
printResult();
return;
}
for (int i = 0; i < numbers.length; i++) { //각 원소를 뽑는다.
result[depth] = numbers[i]; //i번째 원소를 뽑는다.
//중복 가능하므로, visited에 기록할 필요가 없다.
permutation(depth + 1, r - 1);
}
}
private static void printResult() {
for (int number : result) {
System.out.print(number + " ");
}
System.out.println();
}
}
상세 설명
visited배열이 사용되지 않음에 주목하자.- 중복이 가능하므로, 뽑았었던 것을 다음 선택에서 제외할 필요가 없다.
- 하지만 결과를 확인하기 위해선, 뽑았던 숫자를 기록해야 한다.
- 따라서
result배열에 기록하였다.
- 따라서