유니온 파인드 알고리즘

개요

유니온 파인드란?

• 유니온 파인드는 그래프(트리) 알고리즘의 한 종류이다.
• 어떤 두 개의 노드가 같은 그래프에 속해 있는지 판별하는 알고리즘이다.
• 서로소 집합, 상호 베타적 집합이라고도 한다.
• 연산 종류
  • Union 연산
    • 두 개의 트리를 합쳐, 하나의 그래프를 만드는 연산
  • Find 연산
    • 어떤 트리의 루트 노드를 찾는 연산
• 주로 배열을 활용하여, 트리를 표현한다.

지금부터 각 연산에 대해 알아보자.

Union 연산

• 아래 그림과 같이, 각 노드가 아무와도 연결되어 있지 않은 상태라고 생각해보자.

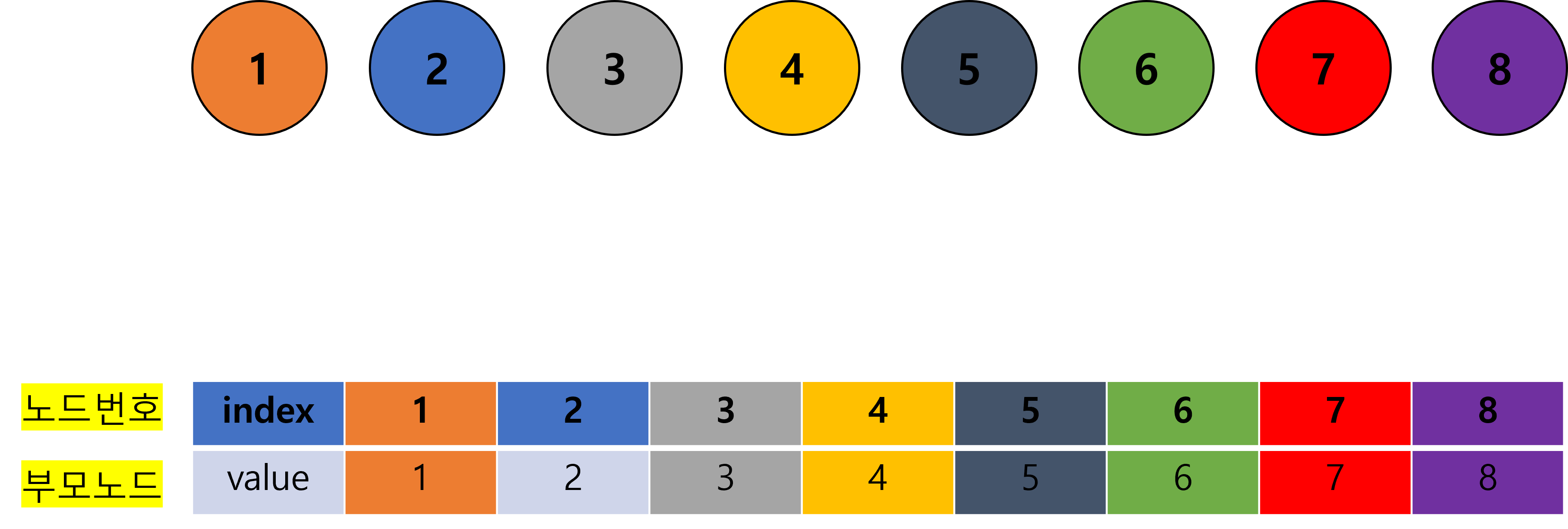
• 배열의 index는 노드의 번호를 나타내고, value는 해당 노드의 부모노드를 나타낸다.

• 이때 우리는 노드를 {1, 2}, {6, 7, 8}과 같이, 연결하고자 한다.

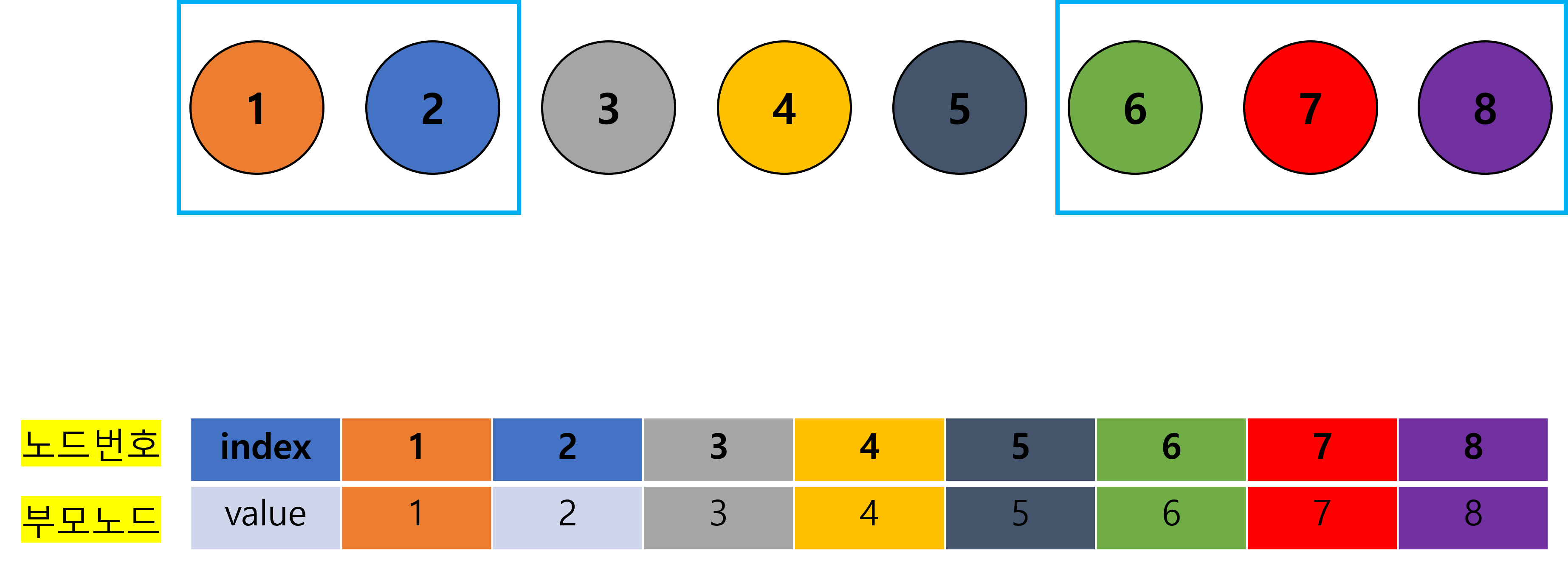
• 배열의 value 값이 해당 노드의 부모 노드를 나타내므로, 각 index의 value 값을 변경하면 된다.
• 이는 아래 그림과 같다.

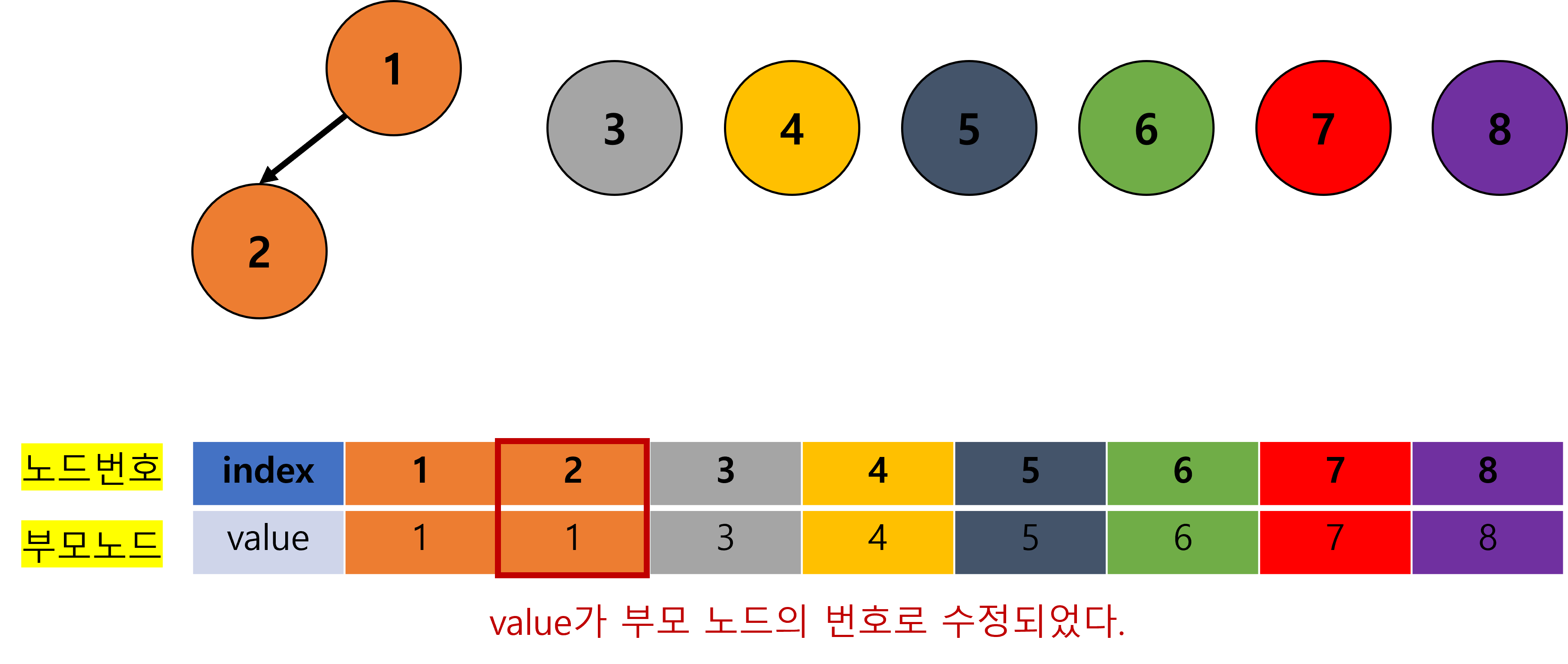
• index 2번의 value 값이 2 -> 1로 변경되었다.

• 이제 나머지에 대해, 마저 수행해보자.

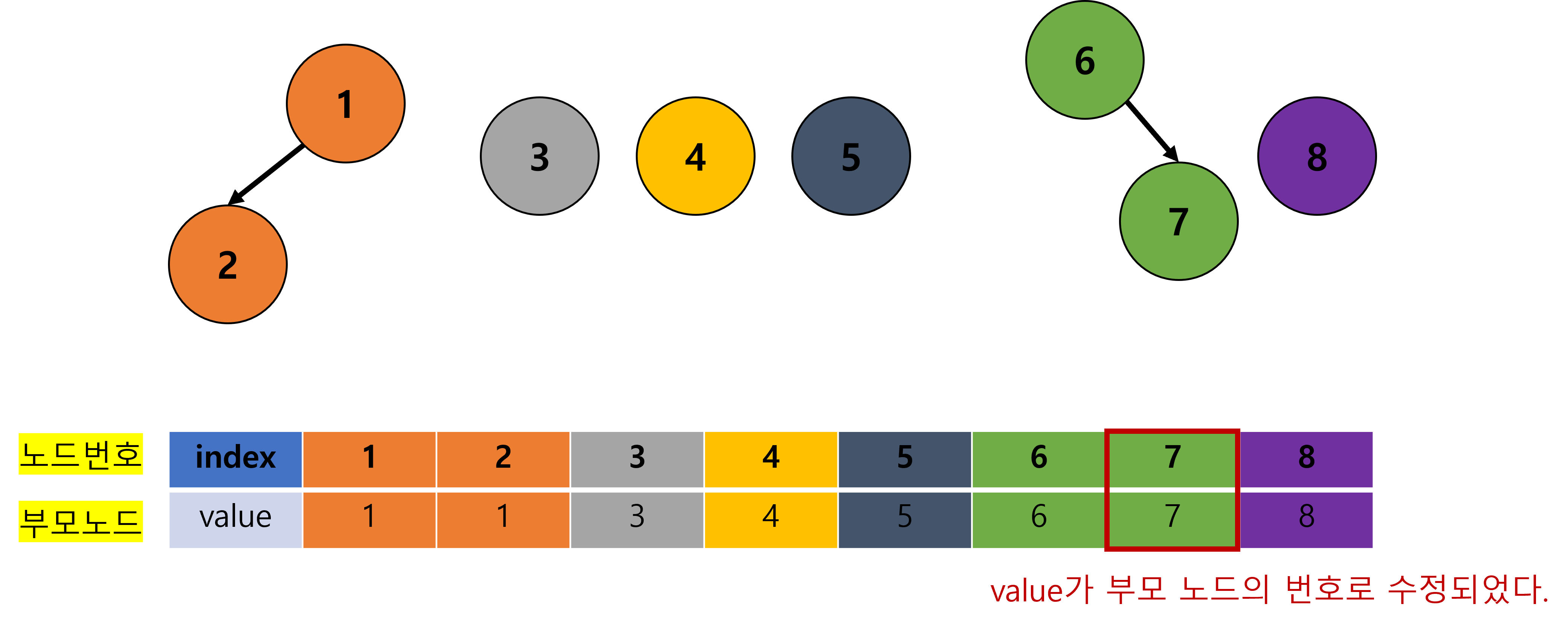
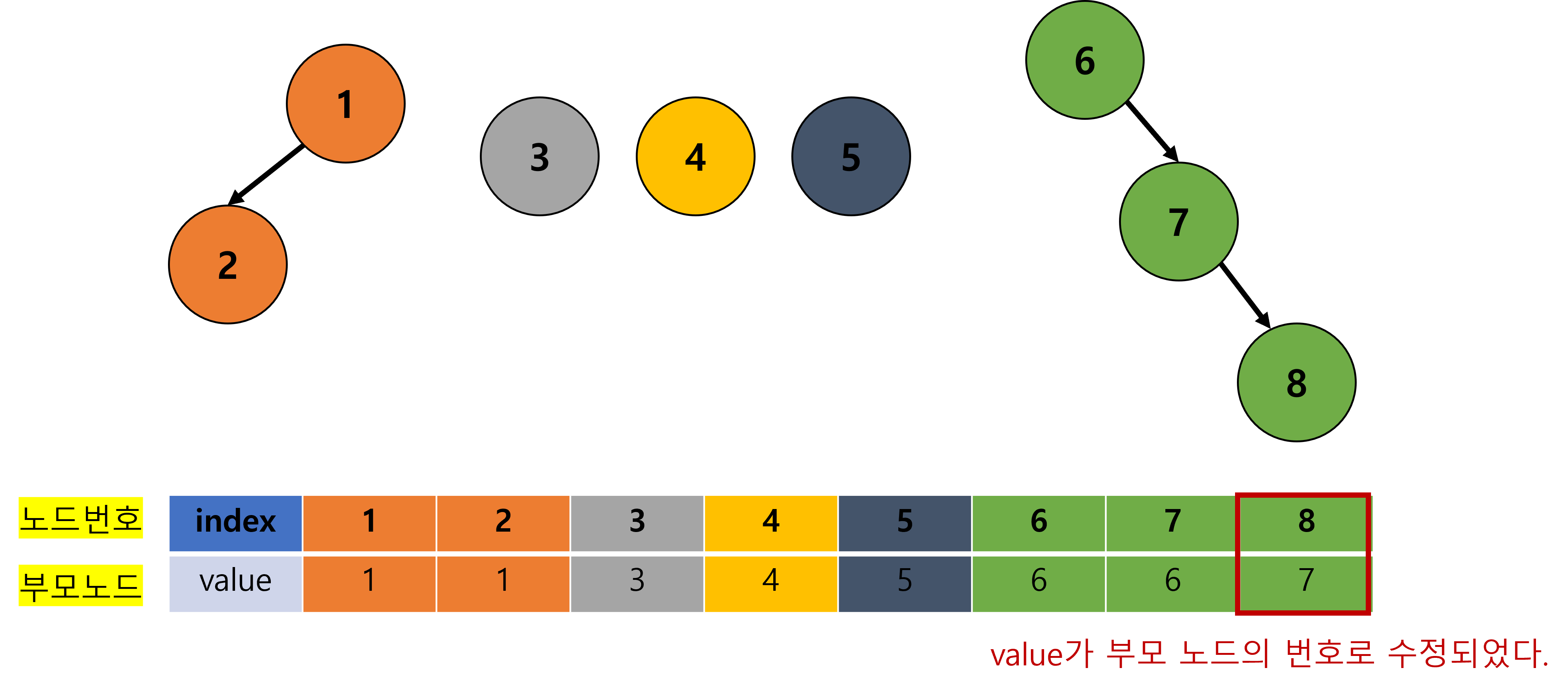
하지만 이러한 방식은 개선의 여지가 남아있다.
Find 연산을 통해, 어떤 비효율성이 숨어있는지 확인하고 개선해보자.

Find 연산

• 위에서 만든 그래프에서 노드 8번이 어떤 트리에 속해있는지 확인해보자.

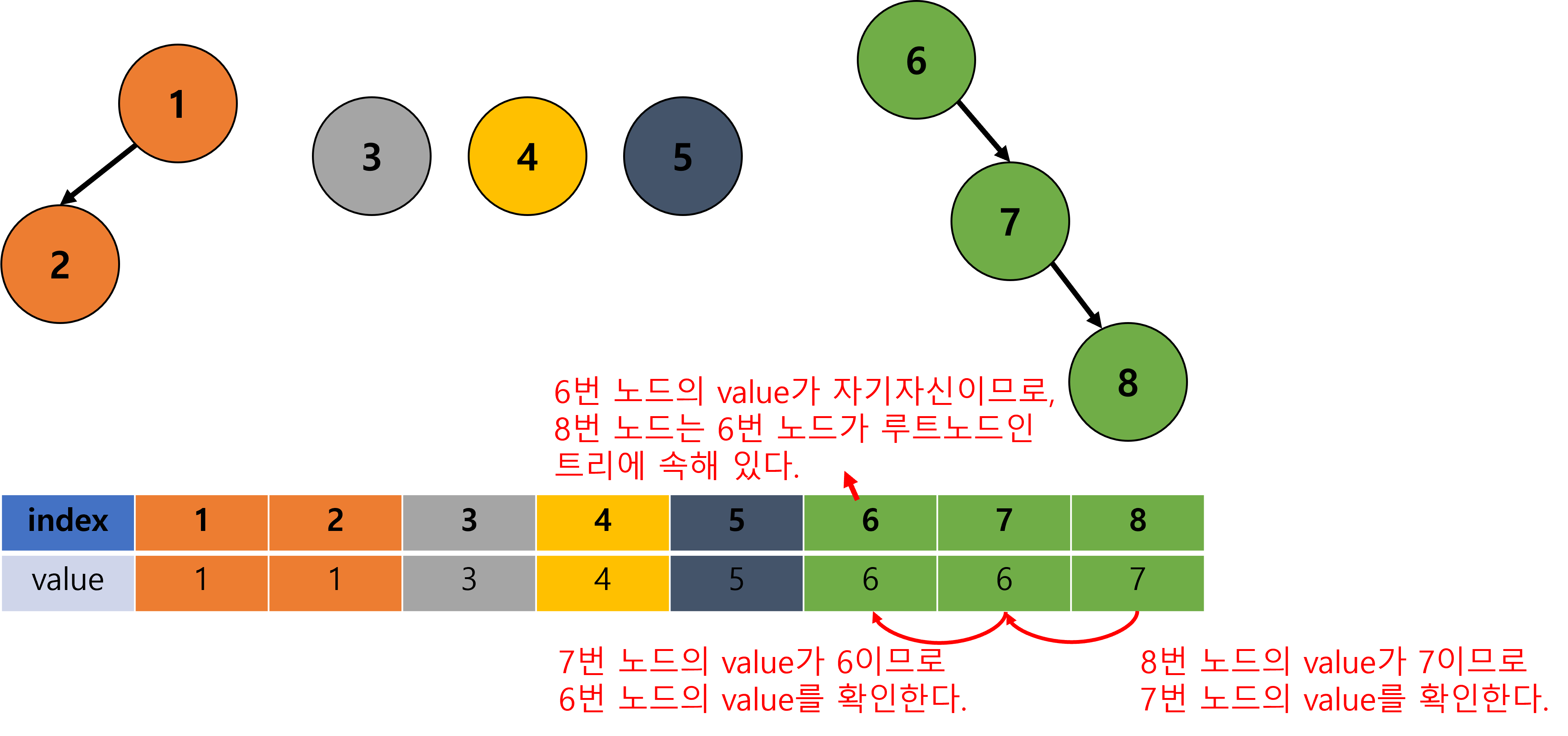
• 이와 같은 절차로, 8번 노드가 어떤 트리에 속해있는지 확인할 수 있다.
• 하지만, 아래와 같이 편중된 상황에서 Find 연산을 수행하게 되면 어떻게 될까?

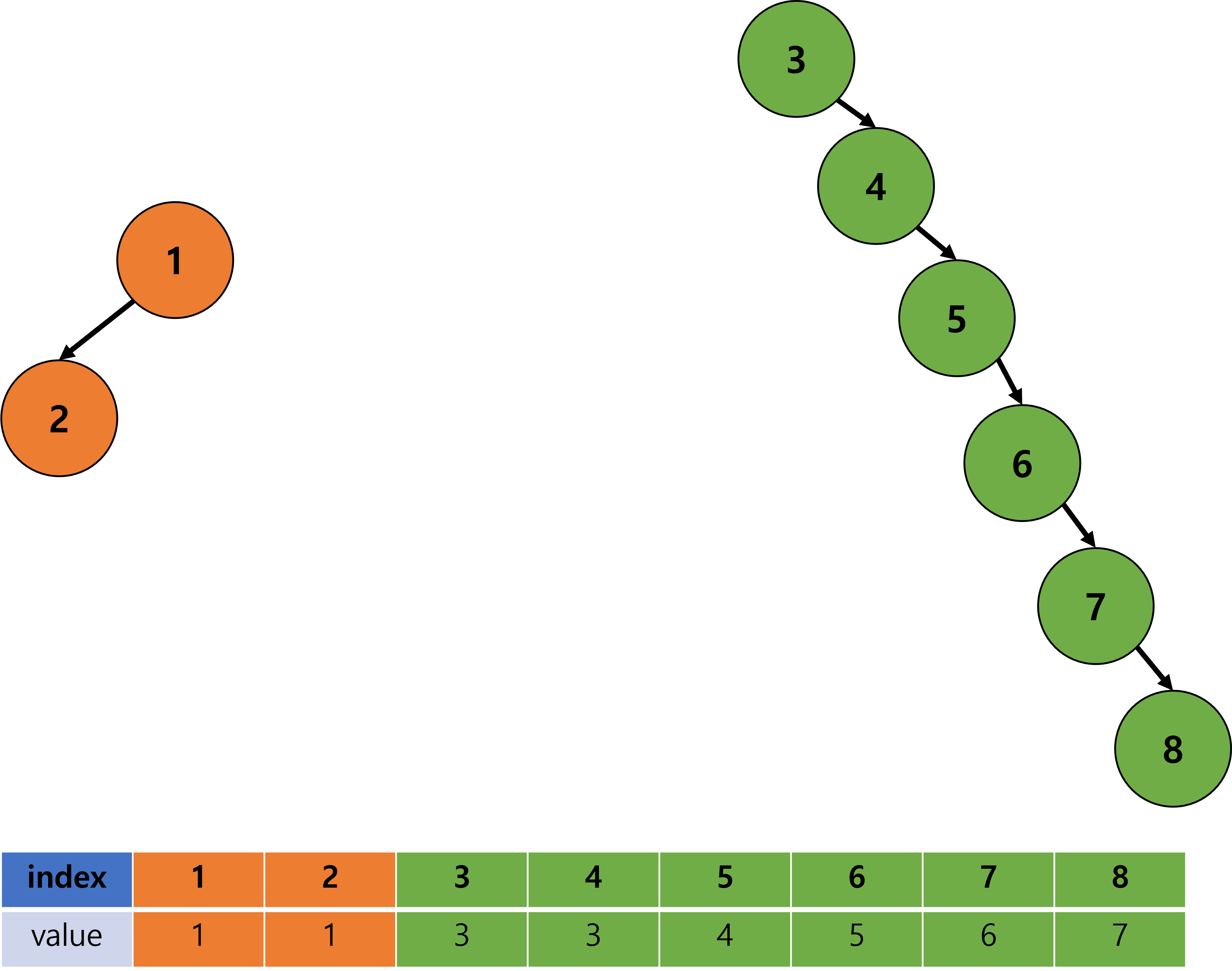
• Find 연산의 시간복잡도는 최악의 경우, O(n) 이다.

  단말 노드부터 탐색을 진행하는 경우

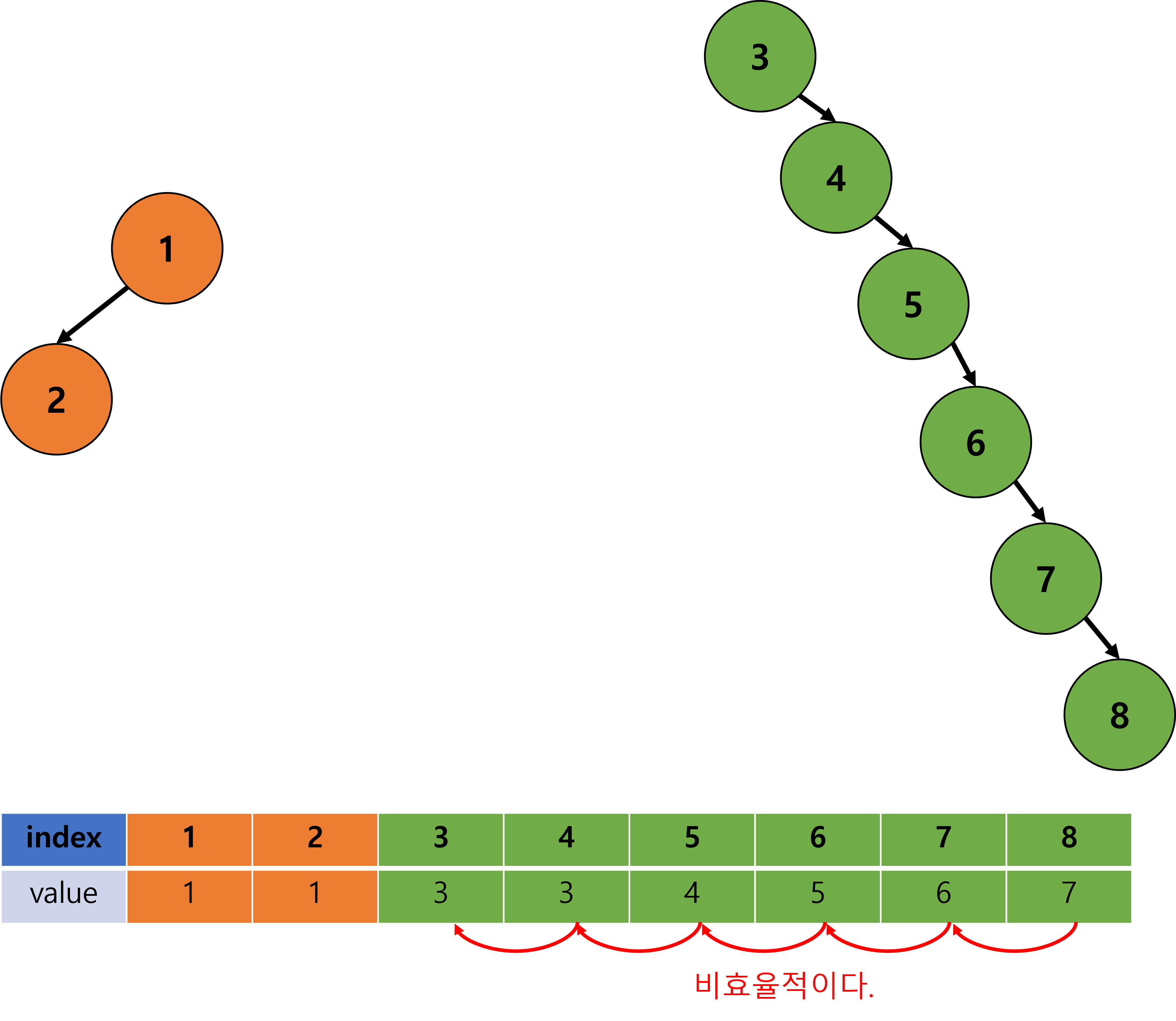
• 이러한 문제를 해결하기 위해선, Union 연산을 개선하면 된다.
• 계속해서 알아보자.

개선된 Union 연산

• 위와 같은 문제를 개선하기 위해, Union 연산을 아래와 같이 수행하도록 하자.
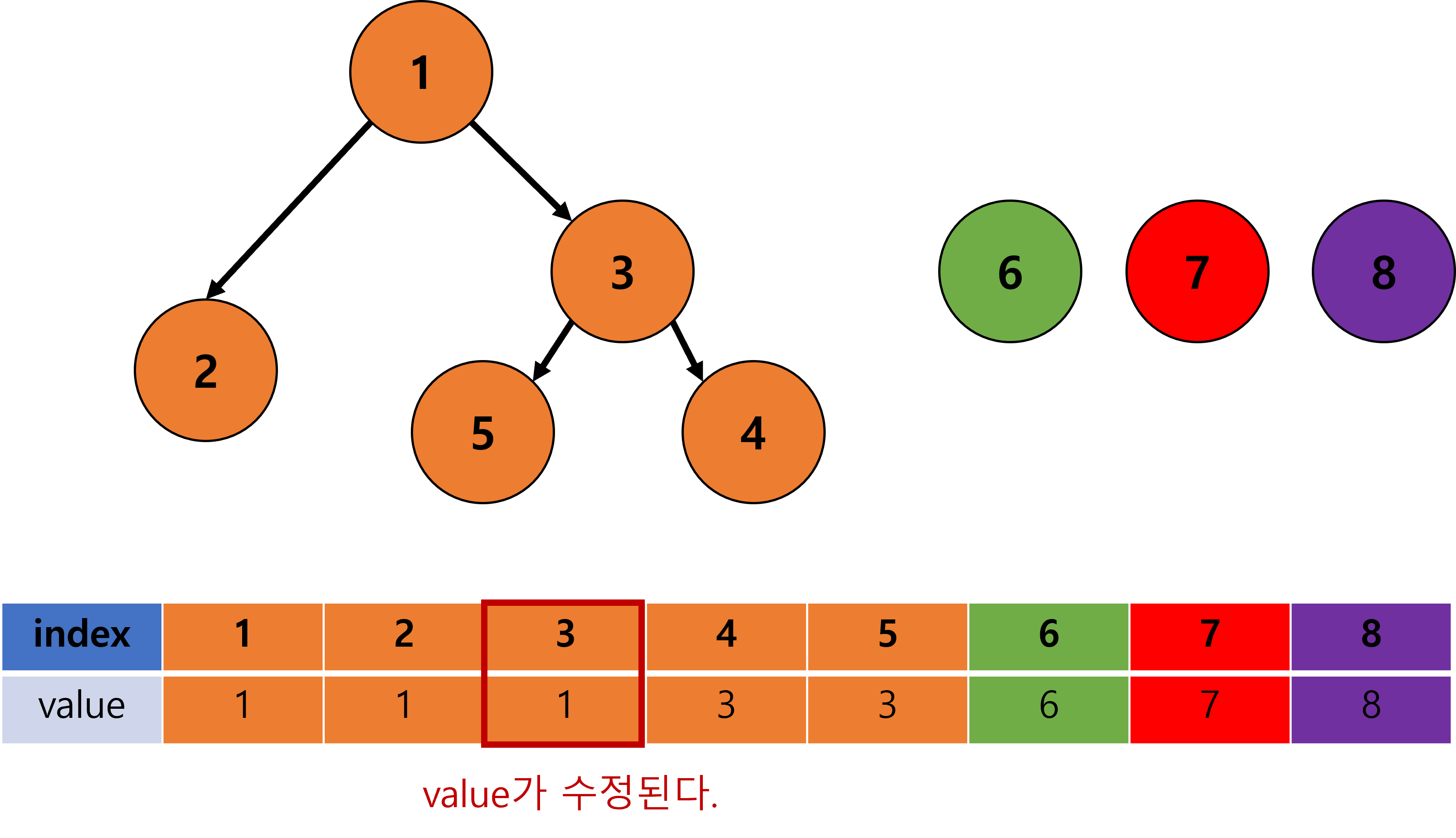
  • 노드의 value를 수정할 때, ‘부모노드의 번호’가 아닌 ‘루트노드의 번호’로 수정
• 예를 들어 {3, 4, 5} 로 묶는 경우, 아래와 같이 수행된다.

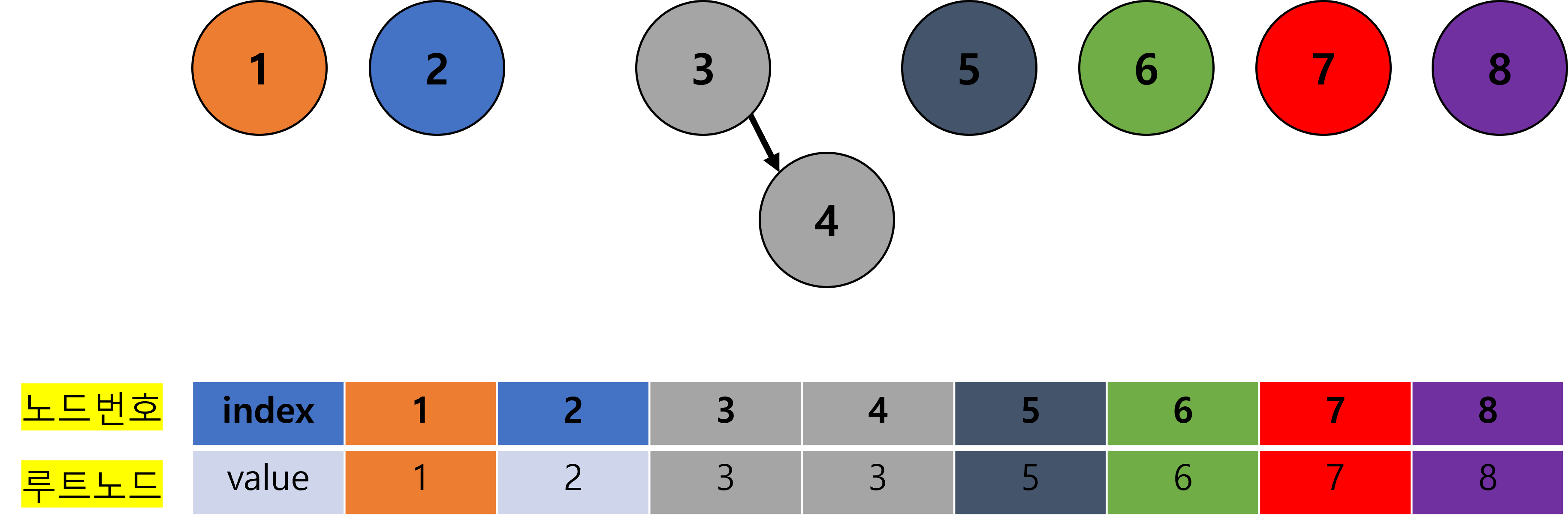
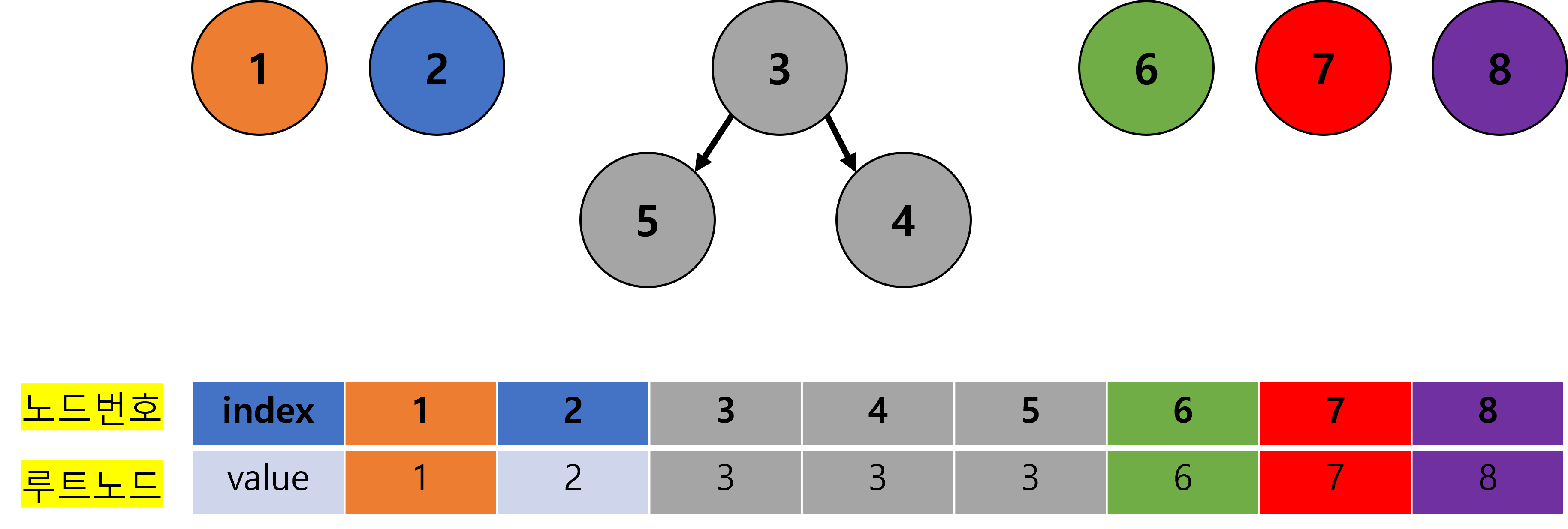
• 위와 같이 수행한다면, Find 연산은 다음과 같이 수행된다.

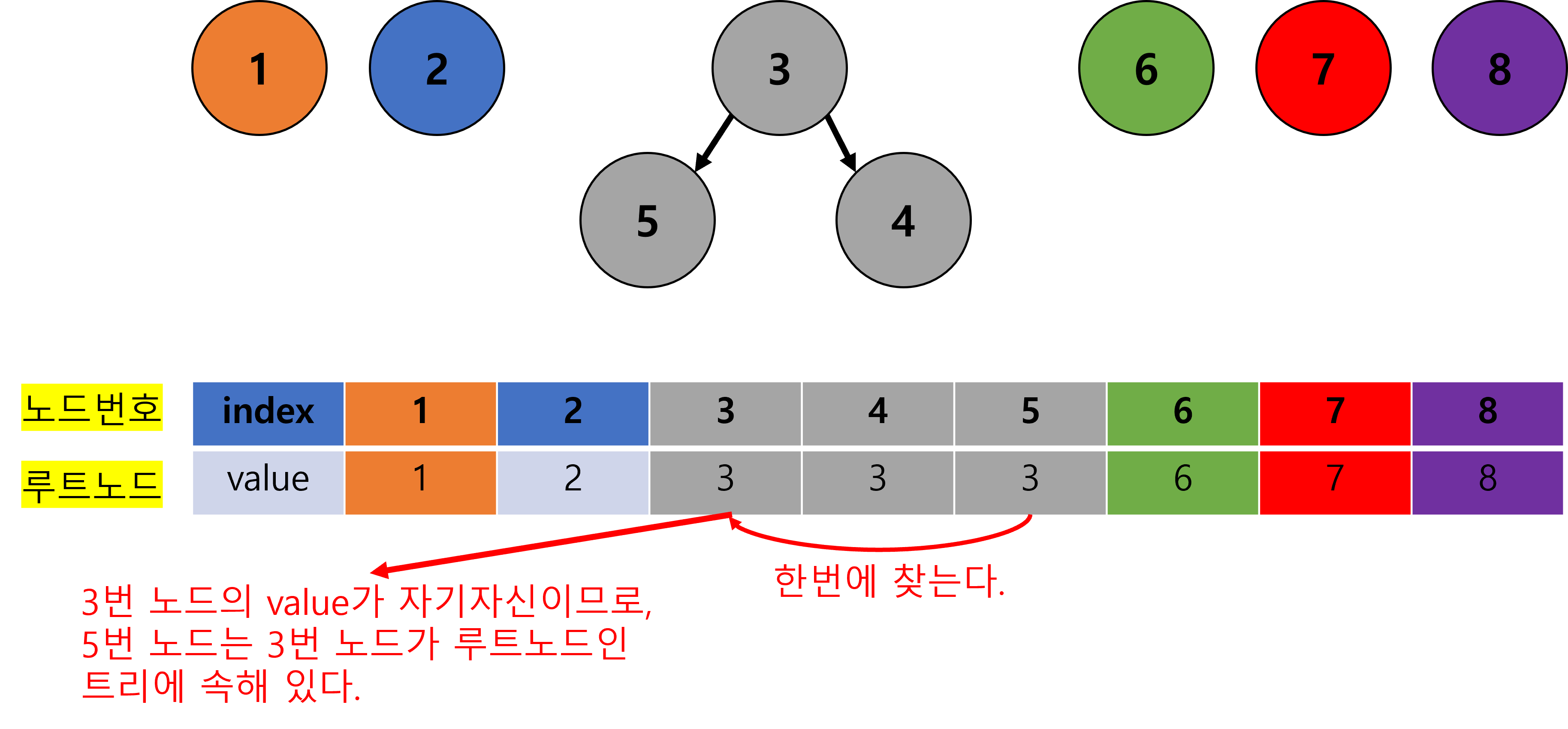
• 이때, {1, 2}로 묶고, {1, 2} 와 {3, 4, 5} 를 묶는다면 아래와 같이 될 것이다.

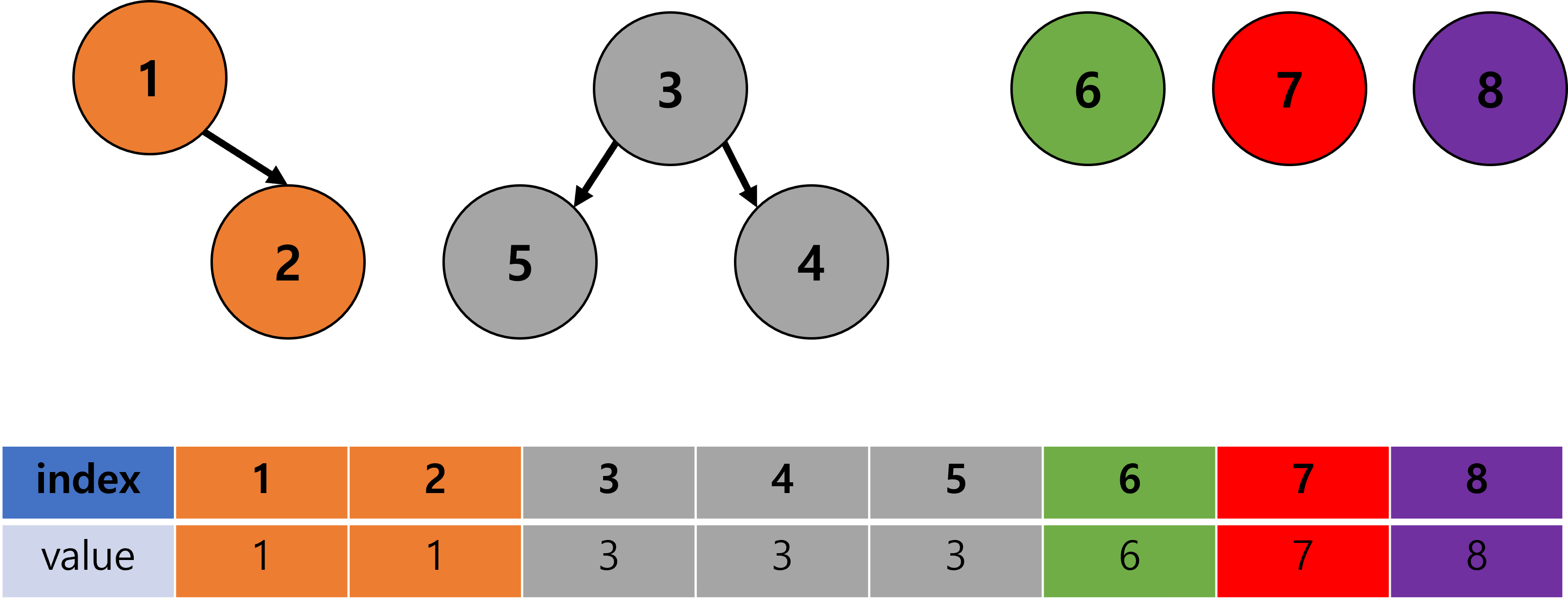
코드

Find 연산 코드

/**
 * Find 메서드
 * @param nodeNumber 찾을 노드번호
 * @return 찾은 루트노드 번호
 */
public int find(int nodeNumber) {
  if (nodeNumber == array[nodeNumber]) { //노드 번호와 값이 같다면
    return nodeNumber; //해당 노드가 루트노드인 트리에 속해있다.
  }

  return find(array[nodeNumber]);
}

Union 연산 코드

/**
 * Union 메서드 (Union은 예약어인 경우가 많아, 보통 merge로 명명한다.)
 * @param x 합칠 노드 1
 * @param y 합칠 노드 2
 */
public void merge(int x, int y) {
  int rootNodeOfX = find(x); //x 노드의 루트노드 번호
  int rootNodeOfY = find(y); //y 노드의 루트노드 번호

  //만약 두 노드의 루트노드가 같다면, 이미 연결되어있는 것이므로 종료
  if (x == y) {
    return;
  }

  //작은 번호가 루트 노드가 되도록
  if (rootNodeOfX < rootNodeOfY) {
    //루트노드 번호로 갱신
    array[rootNodeOfY] = rootNodeOfX;
  } else {
    //루트노드 번호로 갱신
    array[rootNodeOfX] = rootNodeOfY;
  }
}

전체 코드

public class UnionFind {
  int[] array = new int[] {0, 1, 2, 3, 4, 5, 6, 7};

  /**
   * Find 메서드
   * @param nodeNumber 찾을 노드번호
   * @return 찾은 루트노드 번호
   */
  public int find(int nodeNumber) {
    if (nodeNumber == array[nodeNumber]) { //노드 번호와 값이 같다면
      return nodeNumber; //해당 노드가 루트노드인 트리에 속해있다.
    }

    array[nodeNumber] = find(array[nodeNumber]); //경로 압축을 위해, 상단 루트노드로 저장한다.
    return array[nodeNumber];
  }

  /**
   * Union 메서드 (Union은 예약어인 경우가 많아, 보통 merge로 명명한다.)
   * @param x 합칠 노드 1
   * @param y 합칠 노드 2
   */
  public void merge(int x, int y) {
    int rootNodeOfX = find(x); //x 노드의 루트노드 번호
    int rootNodeOfY = find(y); //y 노드의 루트노드 번호

    //만약 두 노드의 루트노드가 같다면, 이미 연결되어있는 것이므로 종료
    if (x == y) {
      return;
    }

    //작은 번호가 루트 노드가 되도록
    if (rootNodeOfX < rootNodeOfY) {
      //루트노드 번호로 갱신
      array[rootNodeOfY] = rootNodeOfX;
    } else {
      //루트노드 번호로 갱신
      array[rootNodeOfX] = rootNodeOfY;
    }
  }

  /**
   * 두 노드가 연결되어있는지 판별하는 연산
   * @param x
   * @param y
   * @return
   */
  public boolean isUnion(int x, int y) {
    int rootNodeOfX = find(x);
    int rootNodeOfY = find(y);

    if (rootNodeOfX == rootNodeOfY) {
      return true;
    }

    return false;
  }
}

실행 코드

public class Main {
  public static void main(String[] args) {
    UnionFind u = new UnionFind();
    u.merge(1, 2);
    u.merge(4, 5);
    u.merge(5, 6);
    u.merge(1, 5);

    System.out.println(u.find(4)); //출력: 1
  }
}