소스코드

다익스트라 알고리즘 - 개선버전

개요

기존버전 vs 개선버전

다익스트라 알고리즘을 간단히 구현하면 시간 복잡도가 O(V^2) 이다.
하지만 지금 다룰 구현방법을 이용하면 다익스트라 최단 경로 문제를 최악의 경우에도 시간 복잡도 O(ElogV) 를 보장하여 해결할 수 있다.
- 여기서 V 는 노드의 개수이고, E 는 간선의 개수를 의미한다.
간단한 다익스트라 알고리즘은 ‘최단 거리가 가장 짧은 노드’를 찾기 위해서, 매번 최단 거리 테이블을 선형적으로 (모든 원소를 앞에서부터 하나씩) 탐색해야 했다.
개선된 다익스트라 알고리즘에서는 힙 자료구조 를 이용한다. 힙 자료구조를 이용하면 특정 노드까지의 최단 거리에 대한 정보를 힙에 담아서 처리하므로, 출발 노드로부터 가장 거리가 짧은 노드를 더욱 빠르게 찾을 수 있다.
- 이 과정에서 선형 시간이 아닌, 로그 시간이 걸린다.

힙 자료구조와 우선순위 큐

힙 자료구조는 우선순위 큐 를 구현하기 위해 사용하는 자료구조 중 하나이다.
힙 자료구조 종류
- 최대힙: 부모노드의 키값이 자식노드의 키값보다 크거나 같은 완전이진트리, 부모노드Key값 ≥ 자식노드Key값
- 최소힙: 부모노드의 키값이 자식노드의 키값보다 작거나 같은 완전이진트리, 부모노드Key값 ≤ 자식노드Key값
힙 자료구조에서의 시간복잡도
- 자료 삽입시 시간복잡도: O(logN)
- 자료 삭제시(검색시) 시간복잡도: O(logN)
우선순위 큐는 우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 구조이다.

자료구조	추출되는 데이터
스택(Stack)	가장 나중에 삽입된 데이터
큐(Queue)	가장 먼저 삽입된 데이터
우선순위 큐(Priority Queue)	가장 우선순위가 높은 데이터

대부분의 프로그래밍 언어에서는 우선순위 큐 라이브러리를 지원하기 때문에 일반적인 코딩 테스트 환경에서 우리가 직접 힙 자료구조부터 작성해서 우선순위 큐를 구현할 일은 없다.
- 대부분의 프로그래밍 언어에서는 우선순위 큐 라이브러리에 데이터의 묶음을 넣으면, 첫 번쨰 원소를 기준으로 우선순위를 설정한다.
- 따라서 데이터가 (가치,물건)으로 구성된다면, ‘가치’ 값이 우선순위 값이 되는 것이다.
우선순위 큐를 구현할 때는 내부적으로 최소힙 혹은 최대힙을 이용한다.
- 최소힙을 이용하는 경우: 값이 낮은 데이터가 먼저 삭제된다.
- 최대힙을 이용하는 경우: 값이 큰 데이터가 먼저 삭제된다.

최소 힙을 최대 힙처럼 사용하는 방법?

우선순위에 해당하는 값에 음수 부호(-)를 붙여서 넣었다가, 나중에 우선순위 큐에서 꺼낸 다음에 다시 음수 부호(-)를 붙여서 원래의 값으로 돌리는 방식을 사용할 수 있다.
이러한 테크닉도 실제 코딩 테스트 환경에서는 자주 사용될 수 있다.

자바에서는 기본적으로 최소 힙 을 사용하여 우선순위 큐가 구현되어 있다.

다익스트라 알고리즘에 우선순위 큐 적용하기

우선순위 큐를 적용하여도 다익스트라 알고리즘이 동작하는 기본 원리는 동일하다.
최단 거리를 저장하기 위한 1차원 리스트(최단 거리 테이블)는 기존처럼 그대로 이용한다.
현재 가장 가까운 노드를 저장하기 위한 목적으로만 우선순위 큐를 추가로 이용한다.

다익스트라 알고리즘 동작 방식

출발 노드를 설정한다.
최단 거리 테이블을 초기화하고, 우선순위 큐에 (거리: 0, 노드: 출발노드) 를 넣는다.
우선순위 큐에서 데이터를 꺼낸다. 만약 꺼낸 데이터의 노드가 이미 처리된 적(방문한 적)있다면, 다시 꺼낸다.
꺼낸 노드를 방문 처리한다.
'시작노드'부터 '3번에서 꺼낸 데이터의 노드'에 연결된 노드까지의 최소 거리 를 구하여, 최단 거리 테이블을 갱신한다.
4번에서 갱신된 데이터 (거리, 노드)를 우선순위 큐에 집어넣는다.
3번, 4번, 5번을 순서대로 반복한다.

동작 예시

예시에서 사용할 그래프 형태

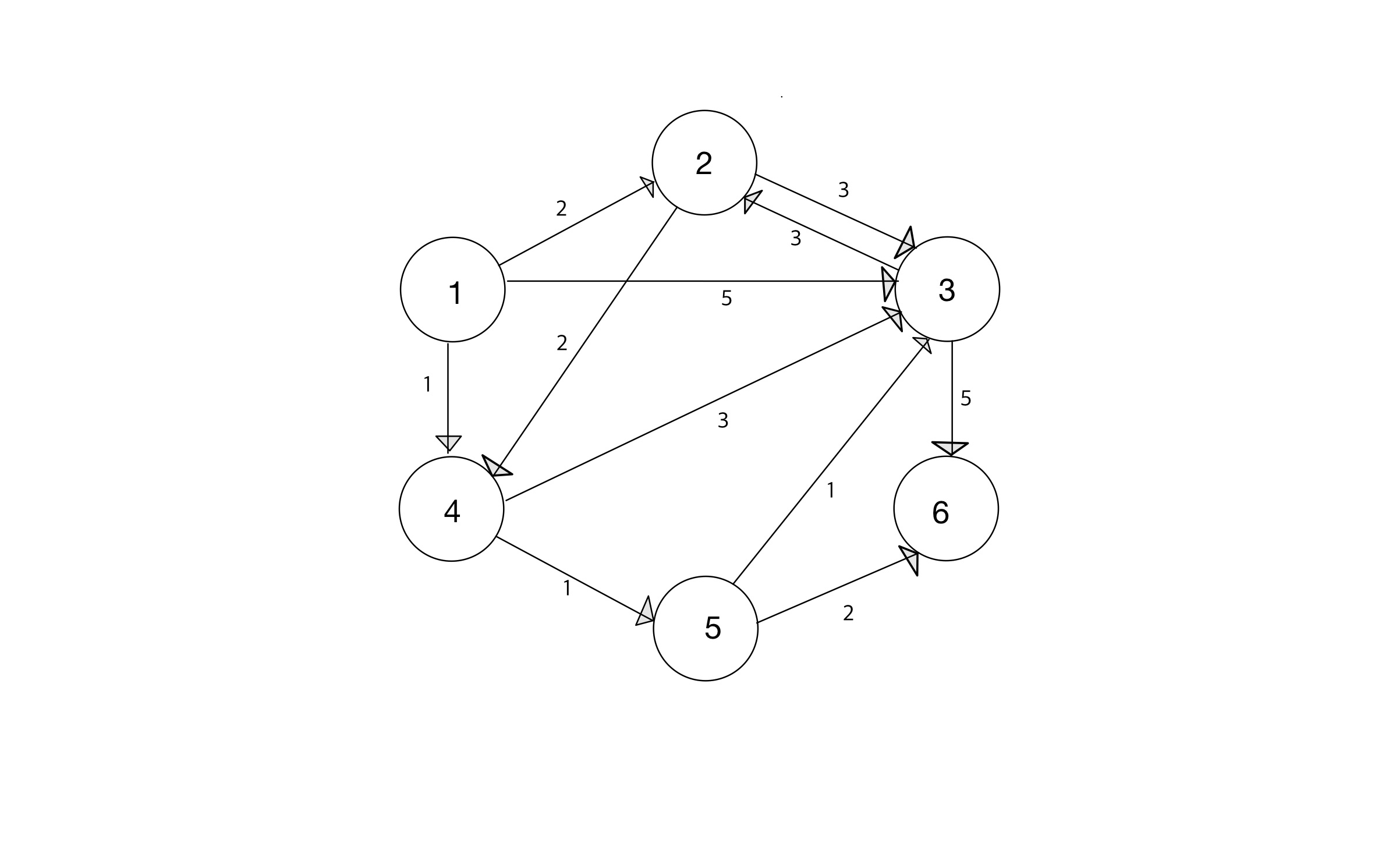
시작노드는 1번 노드이다.

Step 01

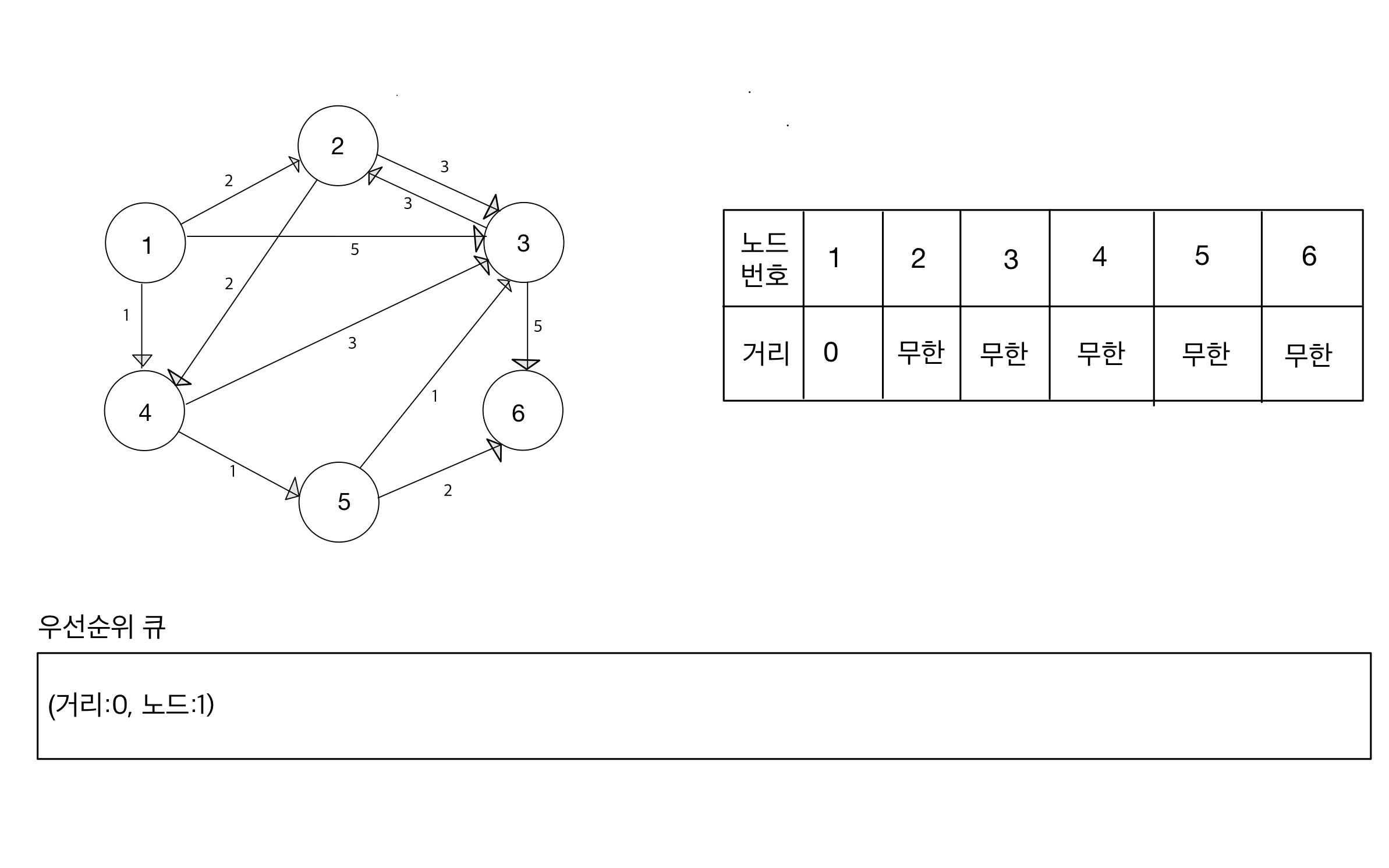
출발 노드에서 출발 노드로의 거리는 0이다.
우선순위 큐에 1번 노드를 포함한 데이터를 넣는다.

Step 02

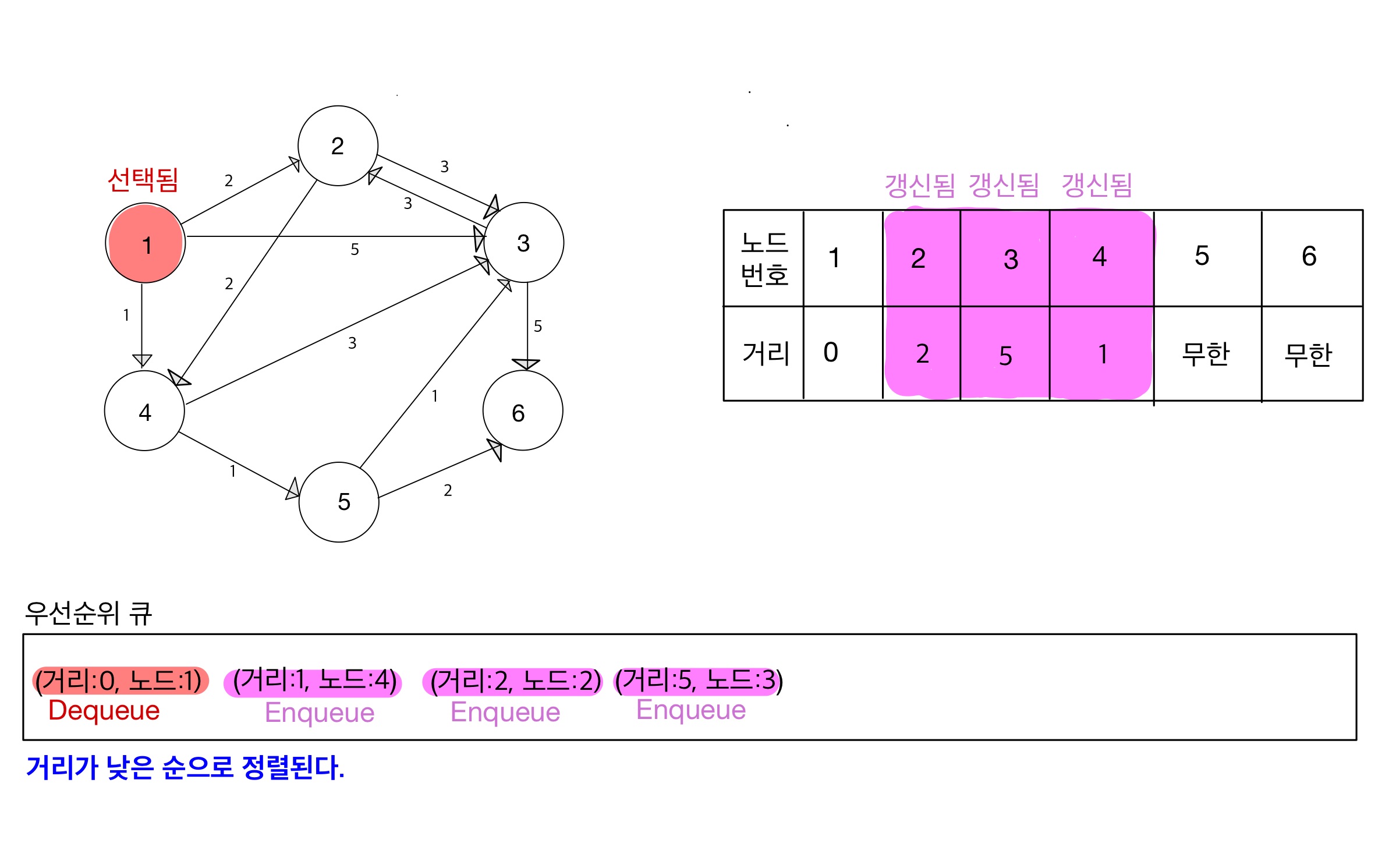
dequeue된 노드 1번이 방문처리되지 않았으므로, ‘시작노드’부터 ‘노드 1번에 연결된 노드들’ 간의 거리를 구한다.
계산된 거리가 최단 거리 테이블의 값보다 작으면 갱신한다.
그리고 갱신된 데이터를 우선순위 큐에 집어넣는다.

Step 03

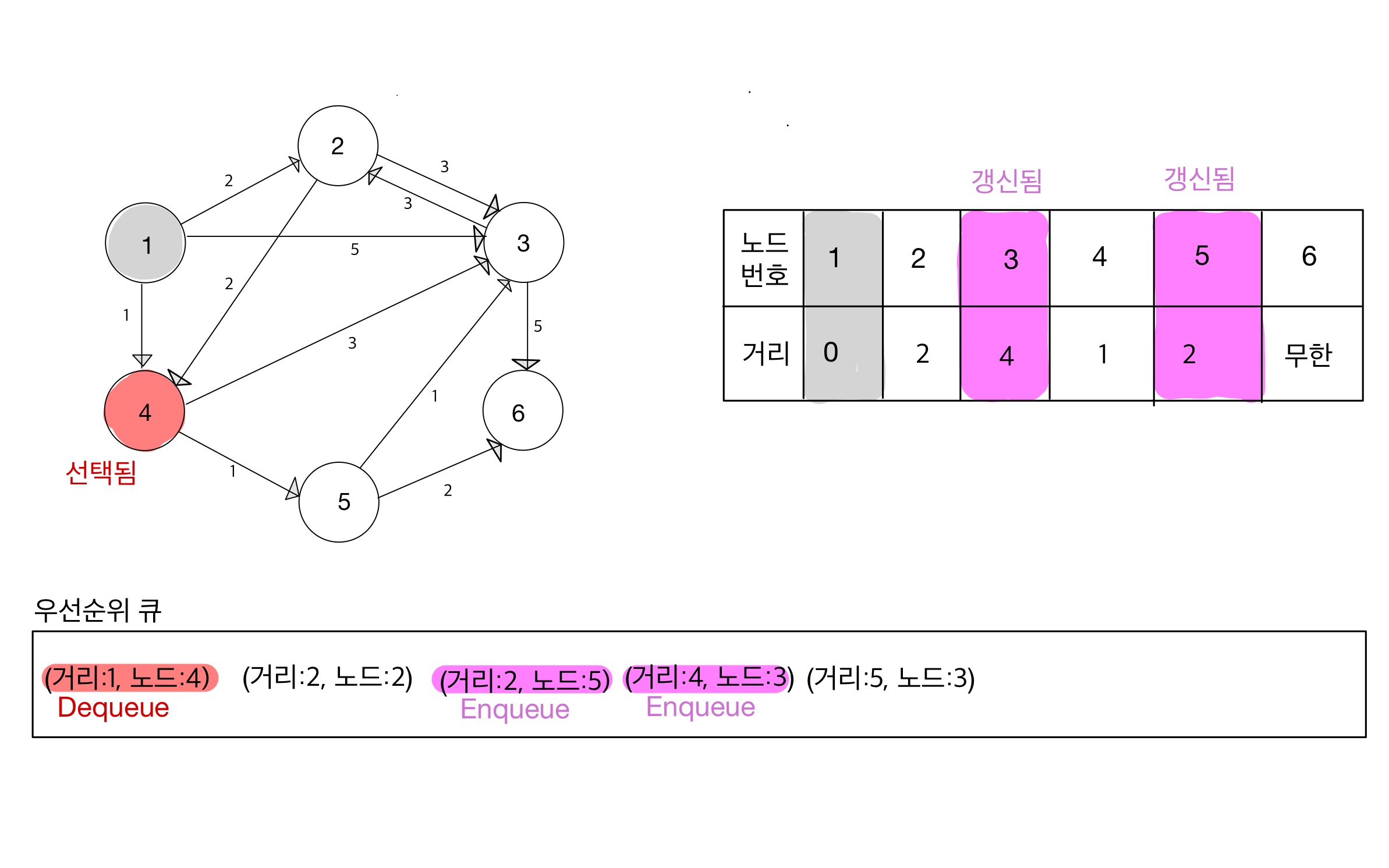
dequeue된 노드 4번이 방문처리되지 않았으므로, ‘시작노드’부터 ‘노드 4번에 연결된 노드들’ 간의 거리를 구한다.
계산된 값이 작다면 최단 거리 테이블을 갱신하고, 갱신된 데이터를 우선순위 큐에 집어넣는다.

Step 04

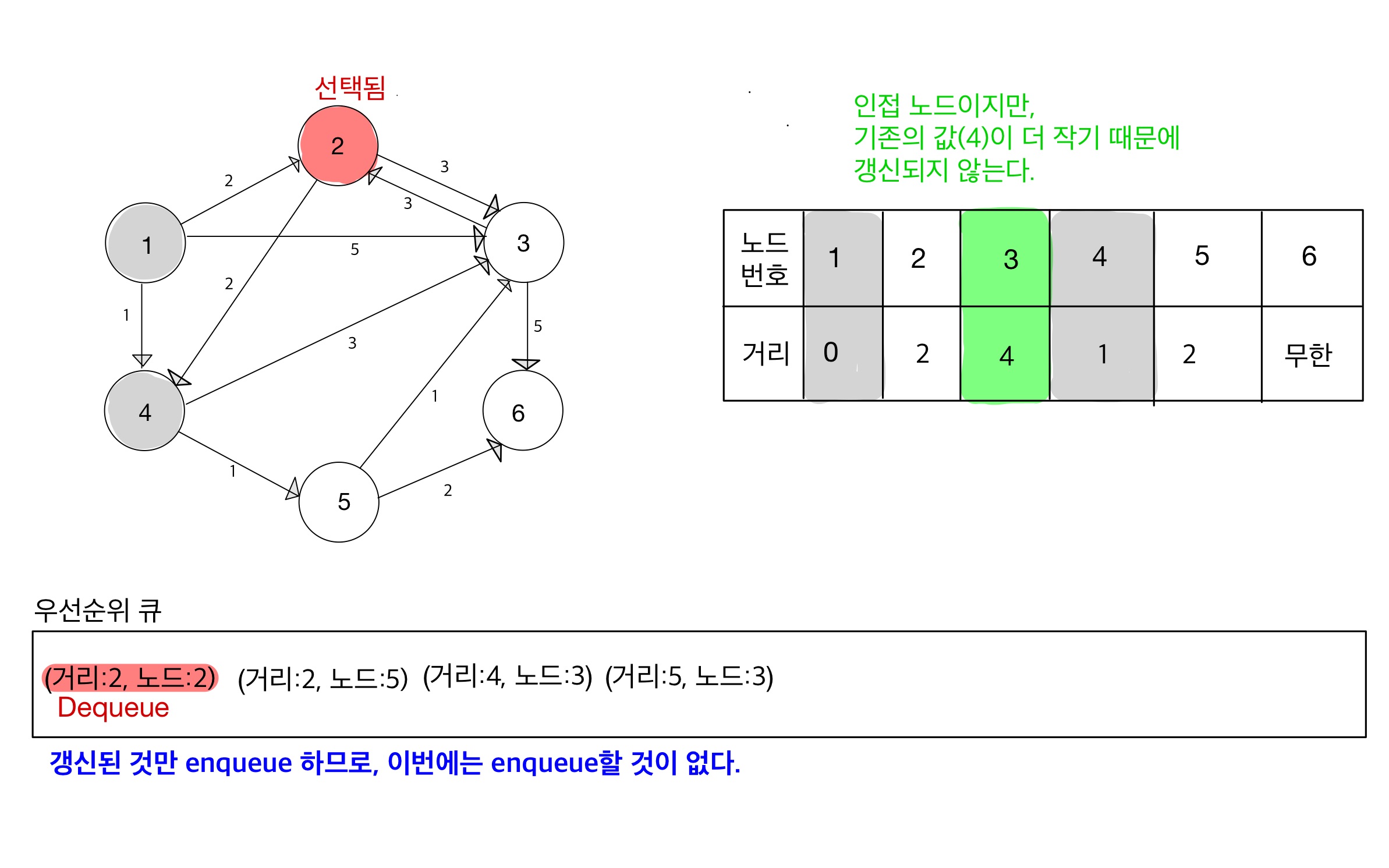
위 그림에선 1 -> 2 -> 3으로 갈 때의 거리 ‘5’보다
기존의 1 -> 4 -> 3 방식의 거리 ‘4’가 더 작기 때문에, 갱신하지 않는다.
갱신되지 않으면 우선순위 큐에 넣지 않는다.

Step 05

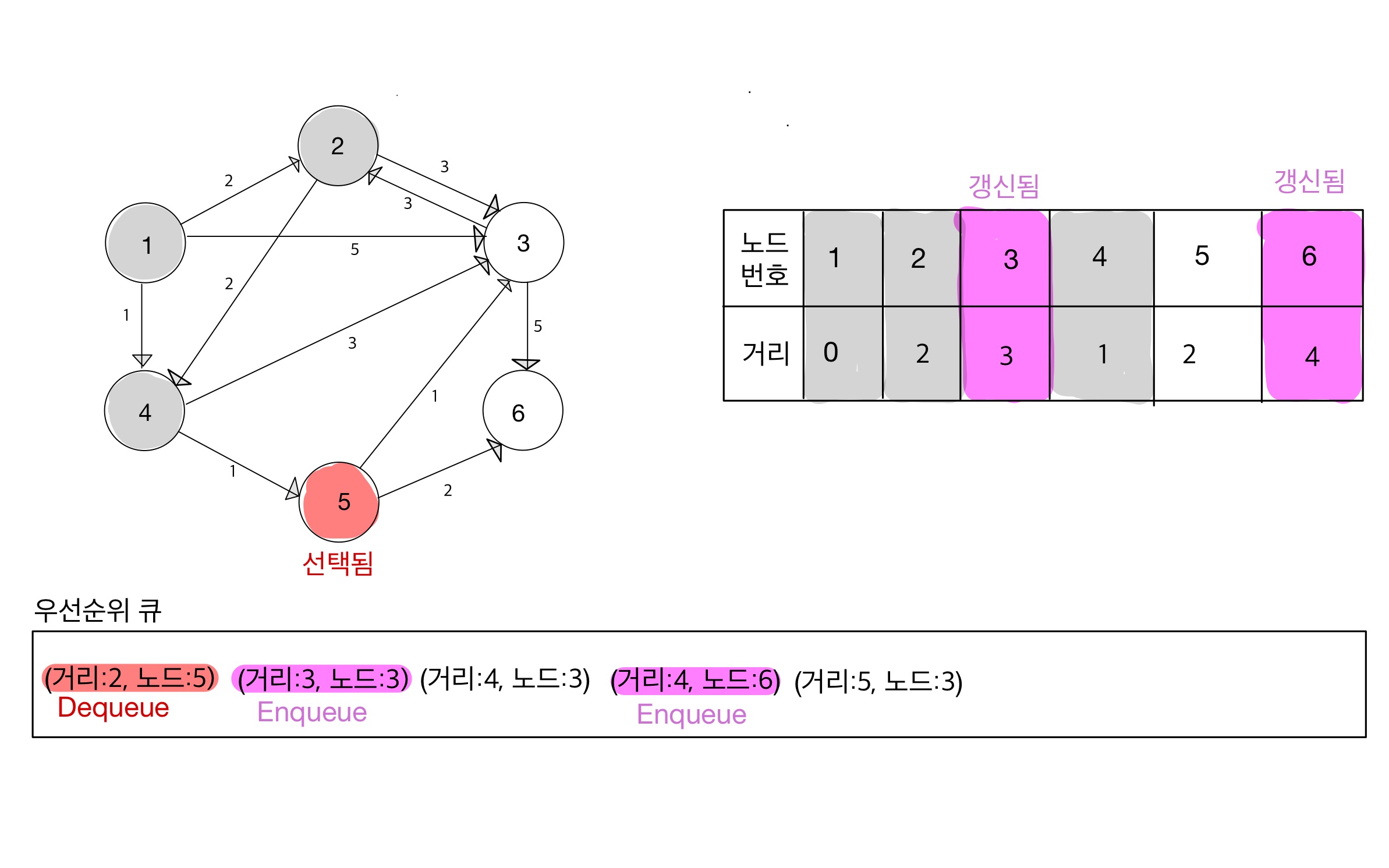
Step 06

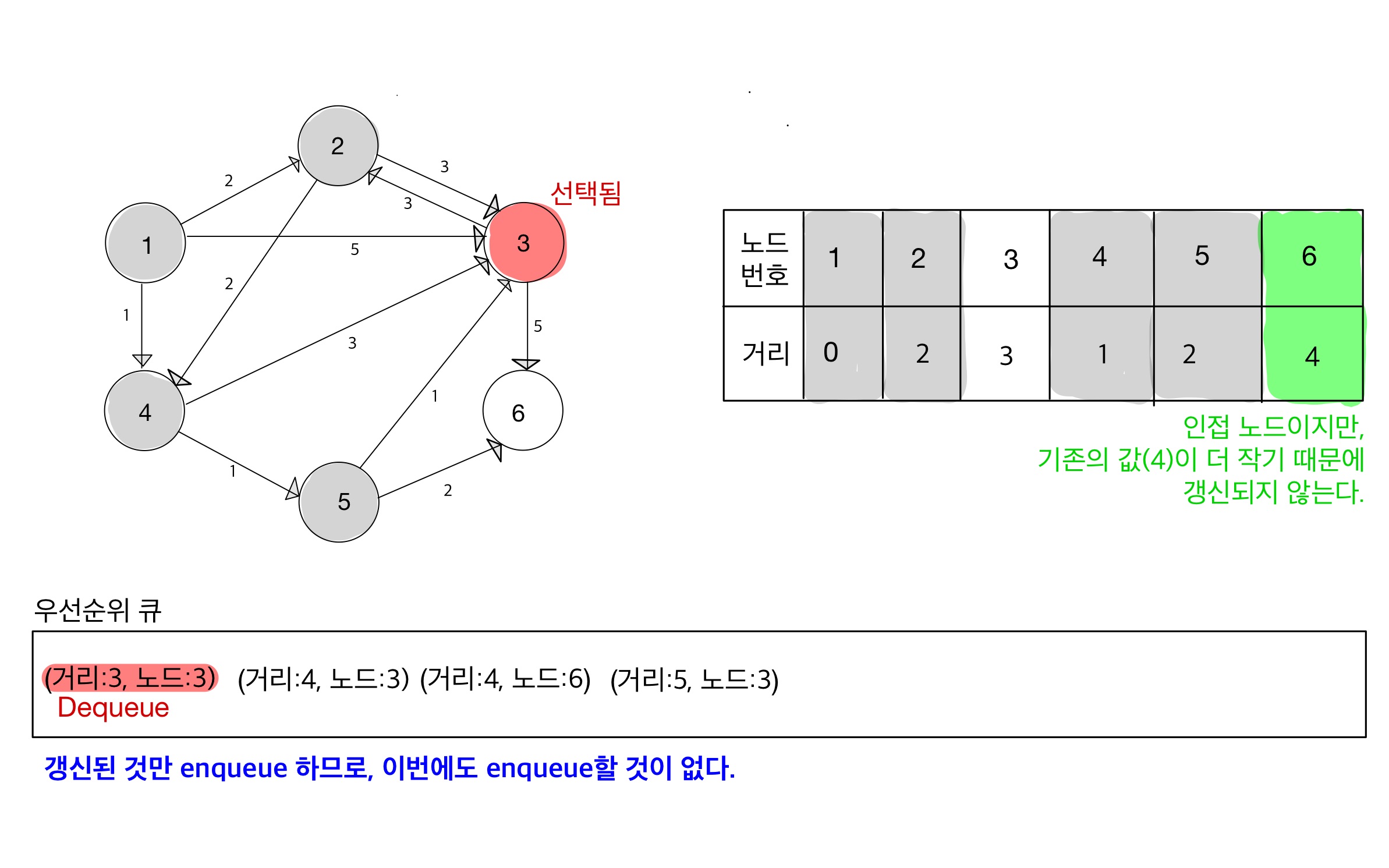
Step 07

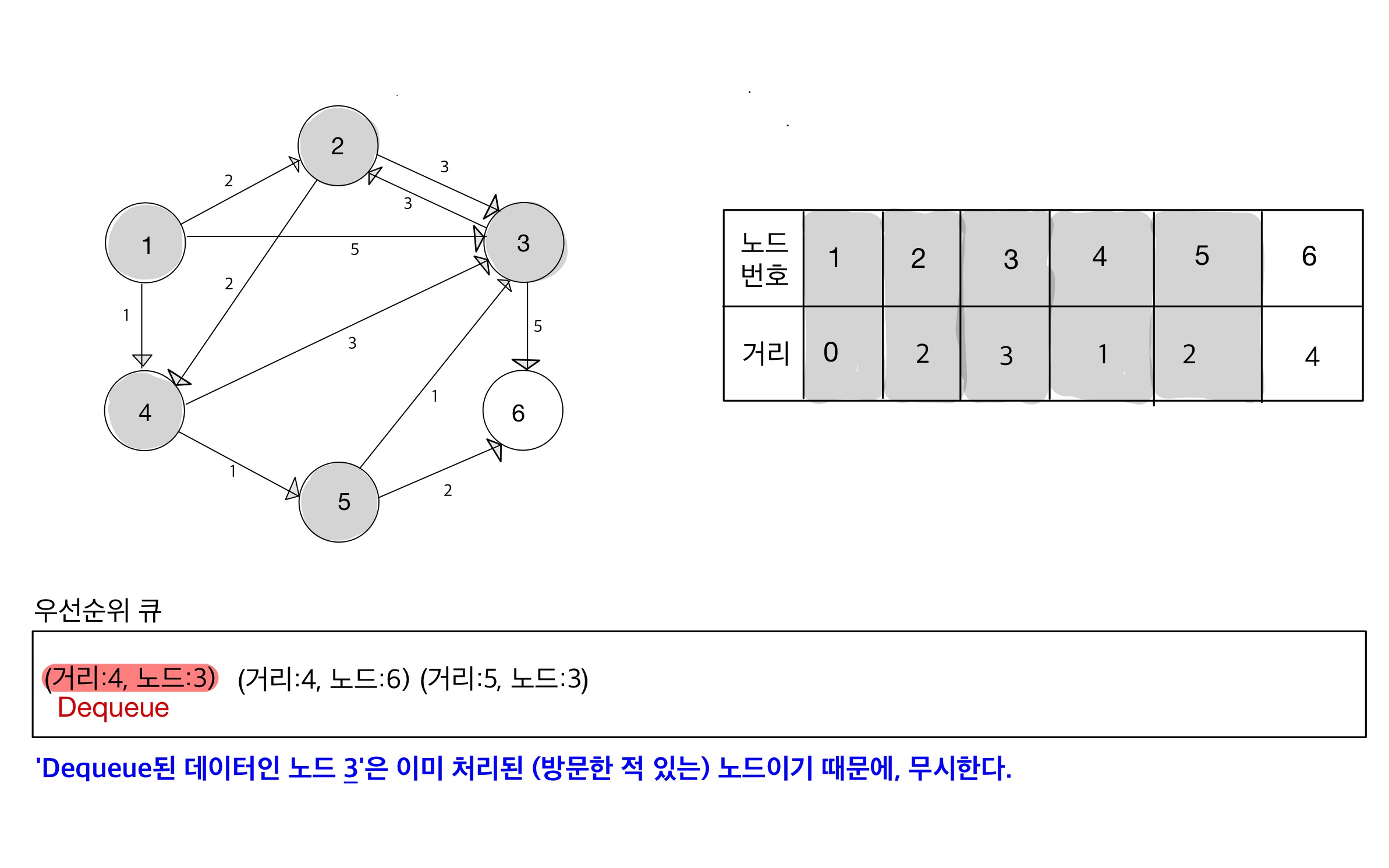
dequeue 된 노드 3은 이미 처리완료 상태(방문 완료 상태) 이기 때문에, 무시한다.

Step 08

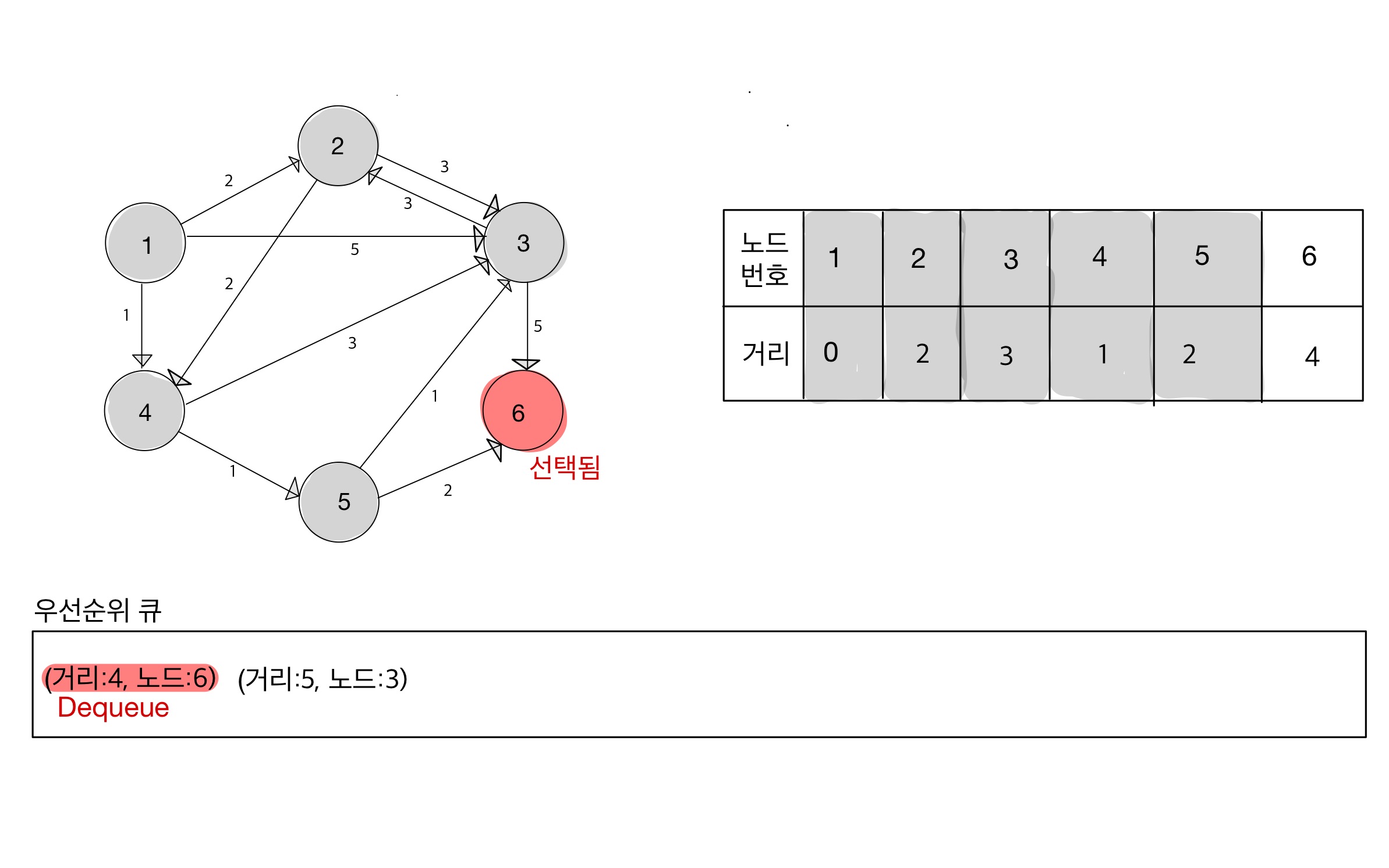
Step 09

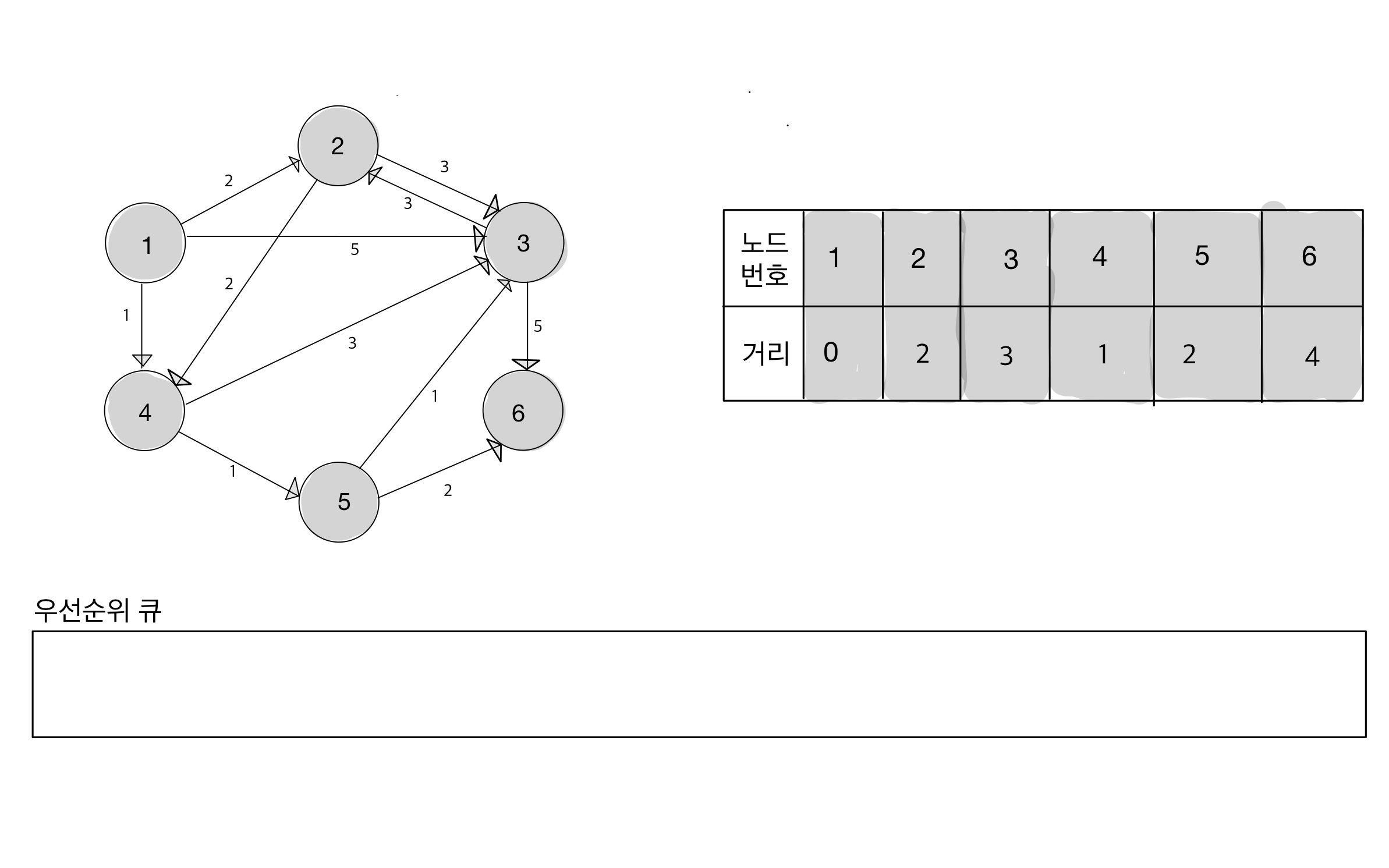
특징

기존 다익스트라 알고리즘 에서 사용한 getShortestNode() 함수를 사용하지 않아도 된다.
- 왜냐하면 ‘최단 거리가 가장 짧은 노드’를 선택하는 과정을 다익스트라 최단 경로 함수 안에서 우선순위 큐를 이용하는 방식으로 대체 할 수 있기 때문이다.

소스코드

다익스트라 알고리즘

public class 다익스트라_개선 {

  private static int sizeOfNode;
  private static int sizeOfEdge;
  private static int startNode;
  private static ArrayList<ArrayList<Node>> graph = new ArrayList<>();
  private static int[] shortestTable = new int[10001];

  /**
   * 실행 메서드
   */
  public static void execute() throws Exception {
    BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
    String s = bf.readLine();
    StringTokenizer st = new StringTokenizer(s);
    sizeOfNode = Integer.parseInt(st.nextToken());
    sizeOfEdge = Integer.parseInt(st.nextToken());
    startNode = Integer.parseInt(bf.readLine());
    for (int i = 0; i <= sizeOfNode; i++) {
      graph.add(new ArrayList<Node>());
    }

    for (int i = 0; i < sizeOfEdge; i++) {
      s = bf.readLine();
      st = new StringTokenizer(s);
      int fromNode = Integer.parseInt(st.nextToken());
      int toNode = Integer.parseInt(st.nextToken());
      int distance = Integer.parseInt(st.nextToken());
      graph.get(fromNode).add(new Node(toNode, distance));
    }

    solution();

    for (int i = 1; i <= sizeOfNode; i++) {

      //시작노드에서 도달할 수 없는 노드인 경우
      if (shortestTable[i] == Integer.MAX_VALUE) {
        System.out.println("INFINITE");
      } else {
        System.out.println(shortestTable[i]);
      }
    }
  }

  /**
   * 다익스트라 알고리즘 메서드
   */
  private static void solution() {
    //우선순위 큐 (최소힙으로 구현되어있다.)
    PriorityQueue<Node> priorityQueue = new PriorityQueue<>();

    //최단거리 테이블 초기화
    Arrays.fill(shortestTable, Integer.MAX_VALUE);
    shortestTable[startNode] = 0;

    priorityQueue.offer(new Node(startNode, 0)); //우선순위 큐에 시작노드 데이터 집어넣기

    //우선순위 큐가 빌때까지 반복
    while (!priorityQueue.isEmpty()) {
      Node node = priorityQueue.poll(); //우선순위 큐에서 거리가 가장 짧은 노드 꺼내기
      int nowNodeIndex = node.getIndex(); //현재 노드 index
      int nowNodeDistance = node.getDistance(); //현재 노드 거리

      //최단거리 테이블 값보다 현재노드의 거리가 더 크다면, 해당 노드는 이미 처리가 된 것이다.
      /*
        "우선순위 큐에 저장된 데이터 == 과거에 최소거리 테이블을 갱신할 때 사용된 데이터" 이다.
        그러므로 '우선순위 큐에 저장된 데이터' 보다 현재의 '최소거리 테이블의 데이터' 가 작다면,
        해당 '우선순위 큐에 저장된 데이터' 는 필요없는 값이 된다.
       */
      if (shortestTable[nowNodeIndex] < nowNodeDistance) continue;

      //현재 노드와 연결된 다른 인접한 노드들을 확인
      for (int i = 0; i < graph.get(nowNodeIndex).size(); i++) {
        int nearNodeIndex = graph.get(nowNodeIndex).get(i).getIndex();
        int nearNodeDistance = graph.get(nowNodeIndex).get(i).getDistance();
        int distanceOfStartNodeToNearNode = shortestTable[nowNodeIndex] + nearNodeDistance;

        if (distanceOfStartNodeToNearNode < shortestTable[nearNodeIndex]) {
          shortestTable[nearNodeIndex] = distanceOfStartNodeToNearNode;
          priorityQueue.offer(new Node(nearNodeIndex, distanceOfStartNodeToNearNode));
        }
      } //내부 for문 종료

    } //외부 while문 종료

  }

  /**
   * Comparable 인터페이스를 상속받는다.
   * Comparable 인터페이스: 객체간 비교를 위한 인터페이스
   */
  private static class Node implements Comparable<Node> {
    private int index;
    private int distance;

    public Node(int index, int distance) {
      this.index = index;
      this.distance = distance;
    }

    public int getIndex() {
      return index;
    }

    public int getDistance() {
      return distance;
    }

    //우선순위 큐 내부에서 정렬될 때 사용된다.
    //거리가 짧은 것이 높은 우선순위를 가지도록 설정
    @Override
    public int compareTo(Node other) {
      if (this.distance < other.distance) {
        return -1; //음수 또는 0이면 객체의 자리가 유지된다. (우선순위 큐가 최소힙으로 구성되어있으므로)
      }
      return 1; //양수인 경우에는 두 객체의 자리가 바뀐다. (우선순위 큐가 최소힙으로 구성되어있으므로)
    }
  }
}

if (shortestTable[nowNodeIndex] < nowNodeDistance) 를 통해, 처리했던 노드인지 판단할 수 있는 이유?
- 우선순위 큐에는 ‘과거에 최단거리 테이블을 갱신하며 넣어둔 데이터’ 들이 여러 개 존재한다.
- 이때 데이터를 enqueue할 때, ‘최단거리 테이블이 갱신되었을 경우’에만 enqueue한다는 것 이외의 제약은 없다.
- 따라서 같은 노드가 여러 번 갱신되었을 때, 우선순위 큐에는 동일한 노드를 갖는 데이터가 여러 개 존재한다. 이는 위 ‘동작 예시’ 에서 확인해볼 수 있다.
  - Step02 : ‘노드 3’이 갱신되며 우선순위 큐에 enqueue 되었다.
  - Step03 : ‘노드 3’이 다시 갱신 되며 우선순위 큐에 enqueue 되었다.
  - Step05 : ‘노드 3’이 또 다시 갱신 되며 우선순위 큐에 enqueue 되었다.
  - 따라서 ‘노드 3’ 관련 데이터가 총 3번 enqueue되었고, 우선순위 큐에서 공존하는 상태이다.
- nowNodeDistance 는 우선순위 큐에서 뽑아낸 노드의 거리값이다.
  우선순위 큐는 거리가 가장 작은 것을 dequeue 해주니, nowNodeDistance 는 현재 우선순위 큐에 들어있는 값 중 가장 작은 값이다.
- 그렇다면, shortestTable[nowNodeIndex] < nowNodeDistance 가 뜻하는바는 무엇일까.
  - nowNodeDistance는 현재로써 가장 작은 값이지만, shortestTable[nowNodeIndex] 이 더 작다면 이미 해당 노드가 처리되었다는 것이다.
  - 즉 우선순위 큐에 같은 노드가 여러 개 존재할 수 있으므로, 현재의 nowNodeDistance 보다 더 작은 값을 갖는 데이터가 과거에 이미 dequeue 되어 처리되었었다는 의미이다.

시간복잡도

위 알고리즘은 O(ElogV)의 시간복잡도를 갖는다.
- V : 노드 개수
- E : 간선 개수
노드를 하나씩 꺼내 검사하는 반복문(while문)은 노드의 개수 V 이상의 횟수로는 반복되지 않는다.
또한 V번 반복될 때마다 각각 자신과 연결된 간선들을 모두 확인(for문)한다.
따라서 ‘현재 우선순위 큐에서 꺼낸 노드와 연결된 다른 노드들을 확인’하는 총 횟수는 총 최대 간선의 개수(E)만큼 연산이 수행될 수 있다.
- 즉 전체 다익스트라 최단 경로 알고리즘은 E개의 원소를 우선순위 큐에 넣었다가 모두 빼내는 연산과 매우 유사하다고 볼 수 있다.
간단하게 생각하면 다익스트라 알고리즘의 시간 복잡도는 최대 E개의 간선 데이터를 힙에 넣었다가 다시 빼는 것으로 볼 수 있으므로 O(ElogE)임을 이해할 수 있다.

나동빈, 『이것이 코딩 테스트다』

본 게시글은 위 교재를 기반으로 정리한 글입니다.