소스코드

플로이드 워셜 알고리즘

개요

플로이드 워셜 알고리즘이란?

모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 하는 경우에 사용할 수 있는 알고리즘이다.

다익스트라 vs 플로이드 워셜

다익스트라 알고리즘은 단계마다 최단 거리를 가지는 노드를 하나씩 반복적으로 선택한다. 그리고 해당 노드를 거쳐 가는 경로를 확인하며, 최단 거리 테이블을 갱신하는 방식으로 동작한다.
플로이드 워셜 알고리즘 또한 단계마다 ‘거쳐 가는 노드’를 기준으로 알고리즘을 수행한다.
- 하지만 매번 ‘방문하지 않은 노드 중에서 최단 거리를 갖는 노드’를 찾을 필요가 없다는 점이 다르다.
다익스트라 알고리즘에서는 출발 노드가 1개이므로 다른 모든 노드까지의 최단 거리를 저장하기 위해서 1차원 리스트를 사용했다.
플로이드 워셜 알고리즘은 다익스트라 알고리즘과는 다르게 2차원 리스트에 ‘최단 거리’ 정보를 저장한다는 특징이 있다.
모든 노드에 대하여 다른 모든 노드로 가는 최단 거리 정보를 담아야 하기 때문이다.
다익스트라 알고리즘은 그리디 알고리즘인데, 플로이드 워셜 알고리즘은 다이나믹 프로그래밍이다.
- 노드의 개수가 N이라고 할 때, N번 만큼의 단계를 반복하며 ‘점화식에 맞게’ 2차원 리스트를 갱신하기 때문에 다이나믹 프로그래밍으로 볼 수 있다.

시간복잡도

노드의 개수가 N개일 때 알고리즘상으로 N번의 단계를 수행하며, 단계마다 O(n^2)의 연산을 통해 ‘현재 노드를 거쳐가는’ 모든 경로를 고려한다.
따라서 플로이드 워셜 알고리즘의 시간 복잡도는 O(n^3) 이다.
- 다시 말해, 2차원 리스트를 처리해야 하므로 N번의 단계에서 매번 O(N^2)의 시간이 소요된다.

동작 개요

여기에선 포괄적인 동작에 대해서 설명한다.
자세한 동작 순서는 문서 아래 예시(그림)를 참고하자.

각 단계에서는 해당 노드를 거쳐 가는 경우를 고려한다.
예시) 1번 노드에 대해서 확인하는 단계
- 1번 노드를 중간에 거쳐 지나가는 모든 경우를 고려하면 된다.
  - 즉 A -> 1번 노드 -> B 로 가는 비용을 확인한 후에 최단 거리를 갱신한다.
- 만약 현재 최단 거리 테이블에 A번 노드에서 B번 노드로 이동하는 비용이 3으로 기록되어 있을 때,
  A번 노드에서 1번 노드를 거쳐 B번 노드로 이동하는 비용이 2라는 것이 밝혀지면,
  A번 노드에서 B번 노드로 이동하는 비용을 2로 갱신하는 것이다.
따라서 알고리즘에서는 현재 확인하고 있는 노드를 제외하고, N-1개의 노드 중에서 서로 다른 노드 (A, B)쌍을 선택한다.
이후에 A -> 현재 확인하고 있는 노드 -> B로 가는 비용을 확인한 뒤, 최단 거리를 갱신한다.
- 다시 말해 $_{N-1}P_{2}$ 개의 쌍을 단계마다 반복해서 확인하면 된다.
  이때 $_{N-1}P_{2}$ 는 $O(n^2)$ 이라고 볼 수 있기 때문에, 전체 시간 복잡도는 $O(N^3)$ 이라고 할 수 있다.
k번째 단계(현재 확인 중인 노드가 k일 때)에 대한 점화식
- $D_{ab}=min(D_{ab},D_{ak}+D_{kb})$
- ‘A에서 B로 가는 최소 비용’과 ‘A에서 K를 거쳐 B로 가는 비용’을 비교하여 더 작은 값으로 갱신하겠다는 뜻이다.

플로이드 워셜 알고리즘 동작 방식

최단 거리 테이블을 초기화한다.
K번째 노드를 선택하고, 해당 노드에 대해서 아래 점화식을 적용한다.
- $D_{ab}=min(D_{ab},D_{ak}+D_{kb})$
모든 노드에 대해 2번을 반복한다.

동작 예시

예시에서 사용할 그래프 형태

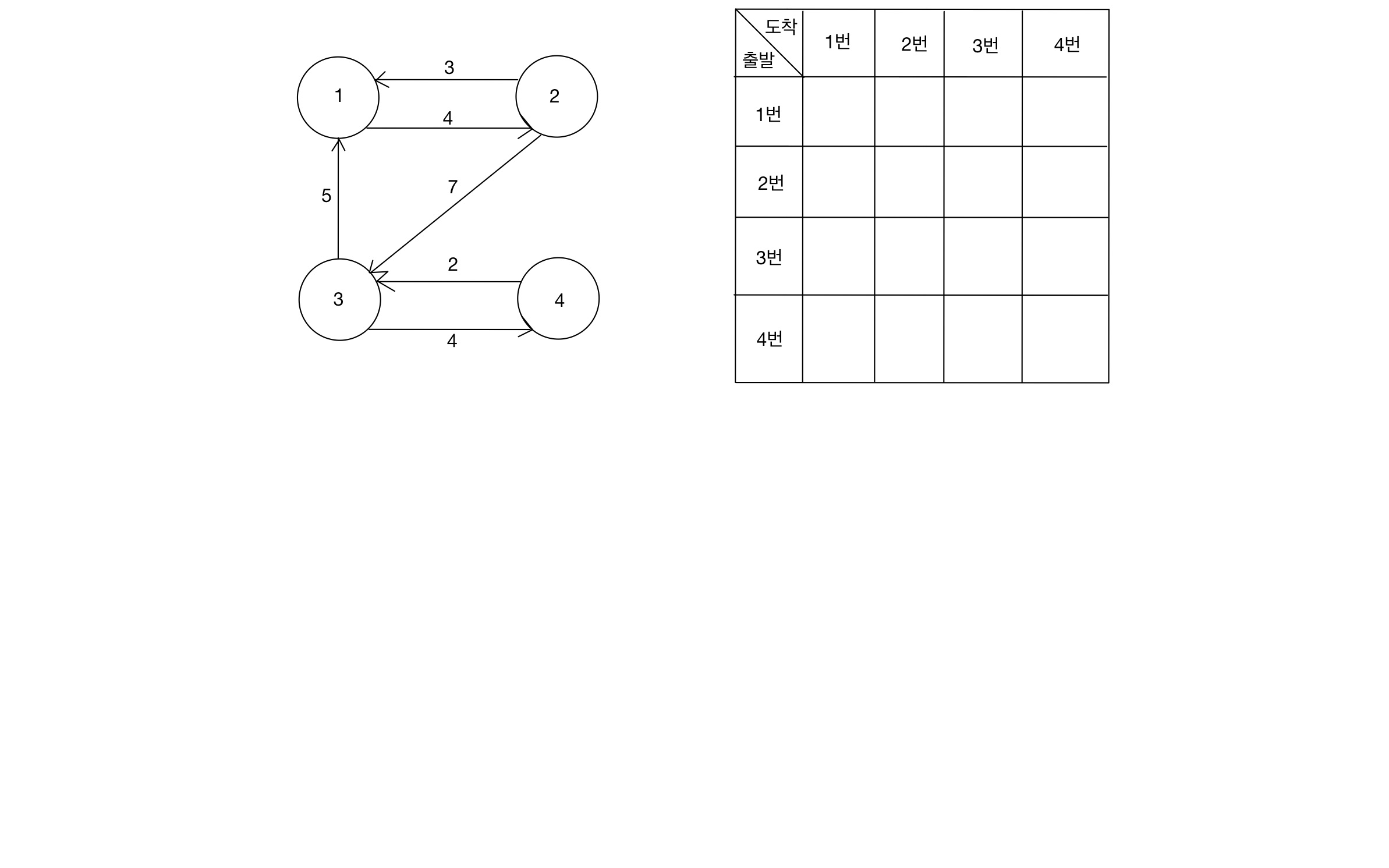
교재의 그래프와 약간 다르니 주의하자!

Step 01

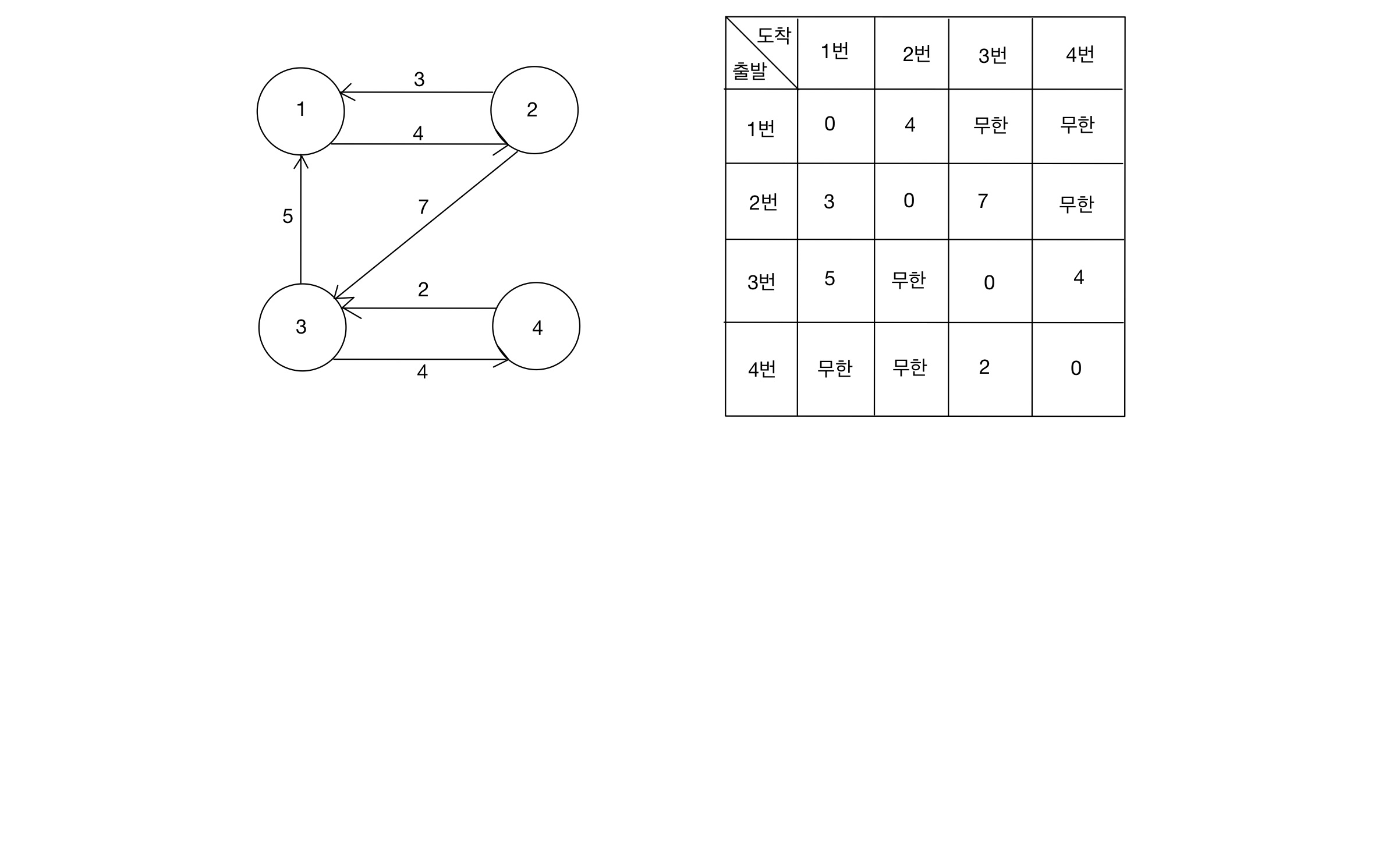
테이블을 초기화한다.
존재하지 않는 간선은 무한으로 표현한다.

Step 02 (K = 1)

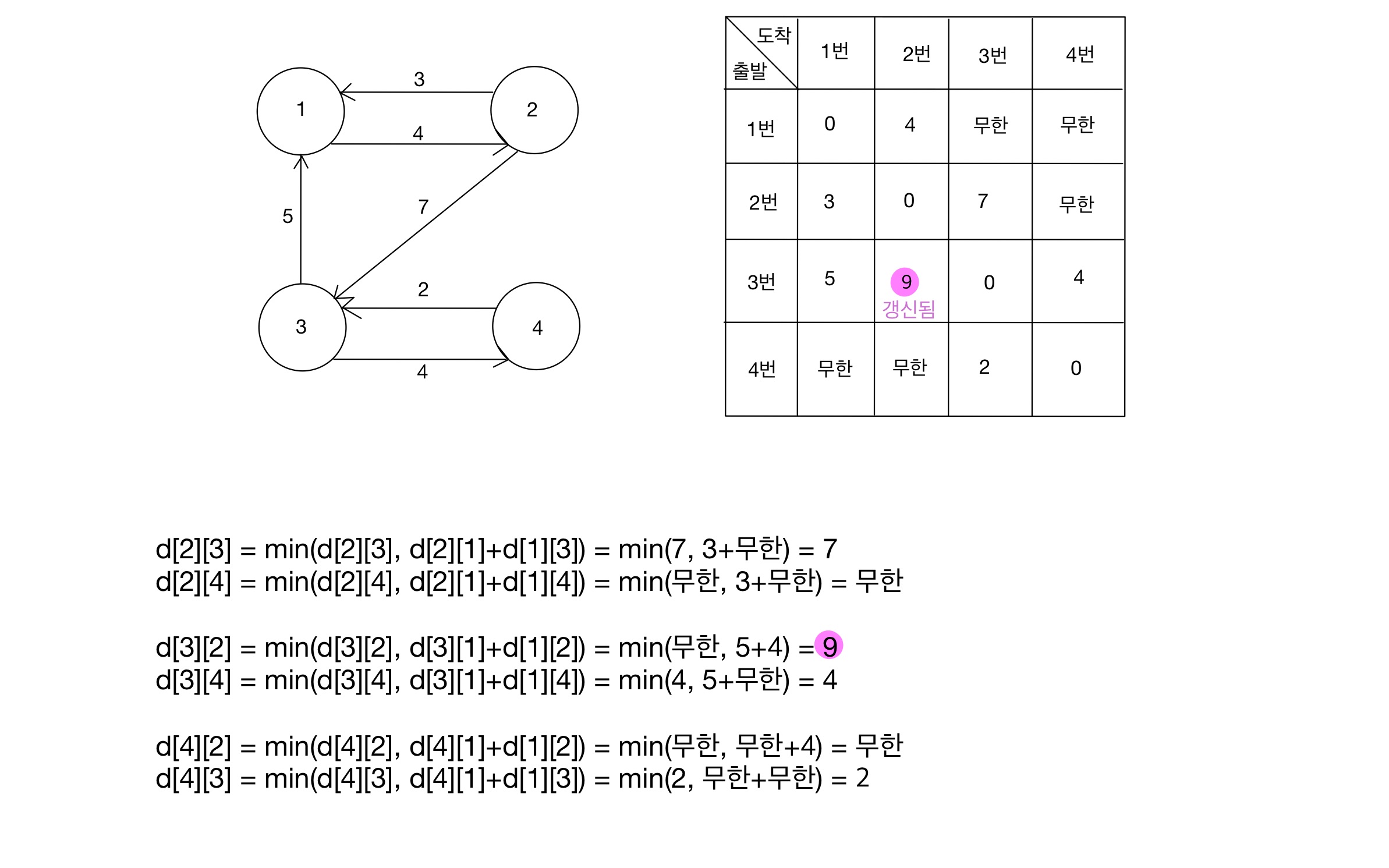
현재 확인 중인 노드(K)가 1일 때, ‘1을 제외한 나머지 노드들에 대해 가능한 모든 경로’에 점화식을 적용한다.

Step 03 (K = 2)

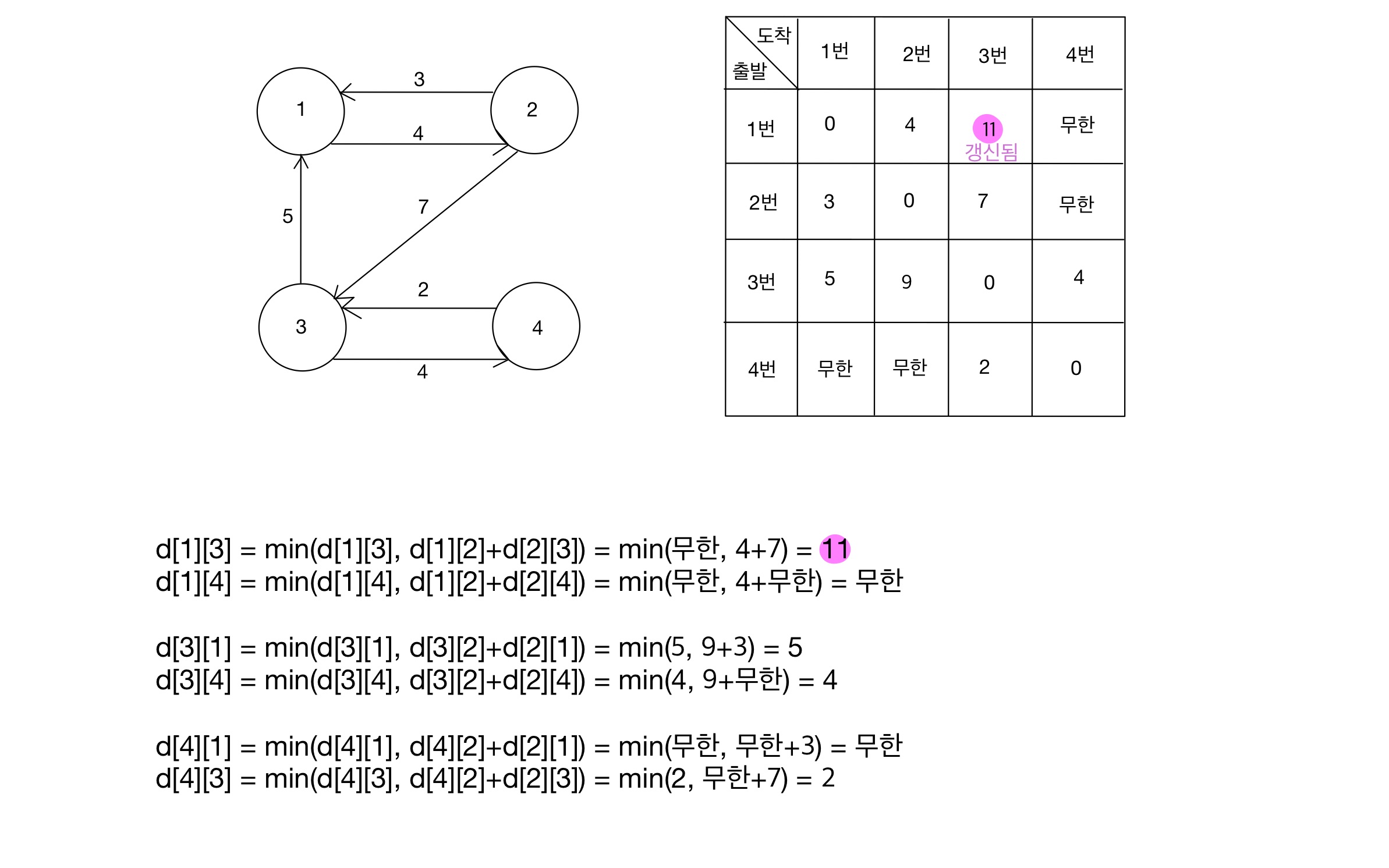
현재 확인 중인 노드(K)가 2일 때, ‘2을 제외한 나머지 노드들에 대해 가능한 모든 경로’에 점화식을 적용한다.

Step 04 (K = 3)

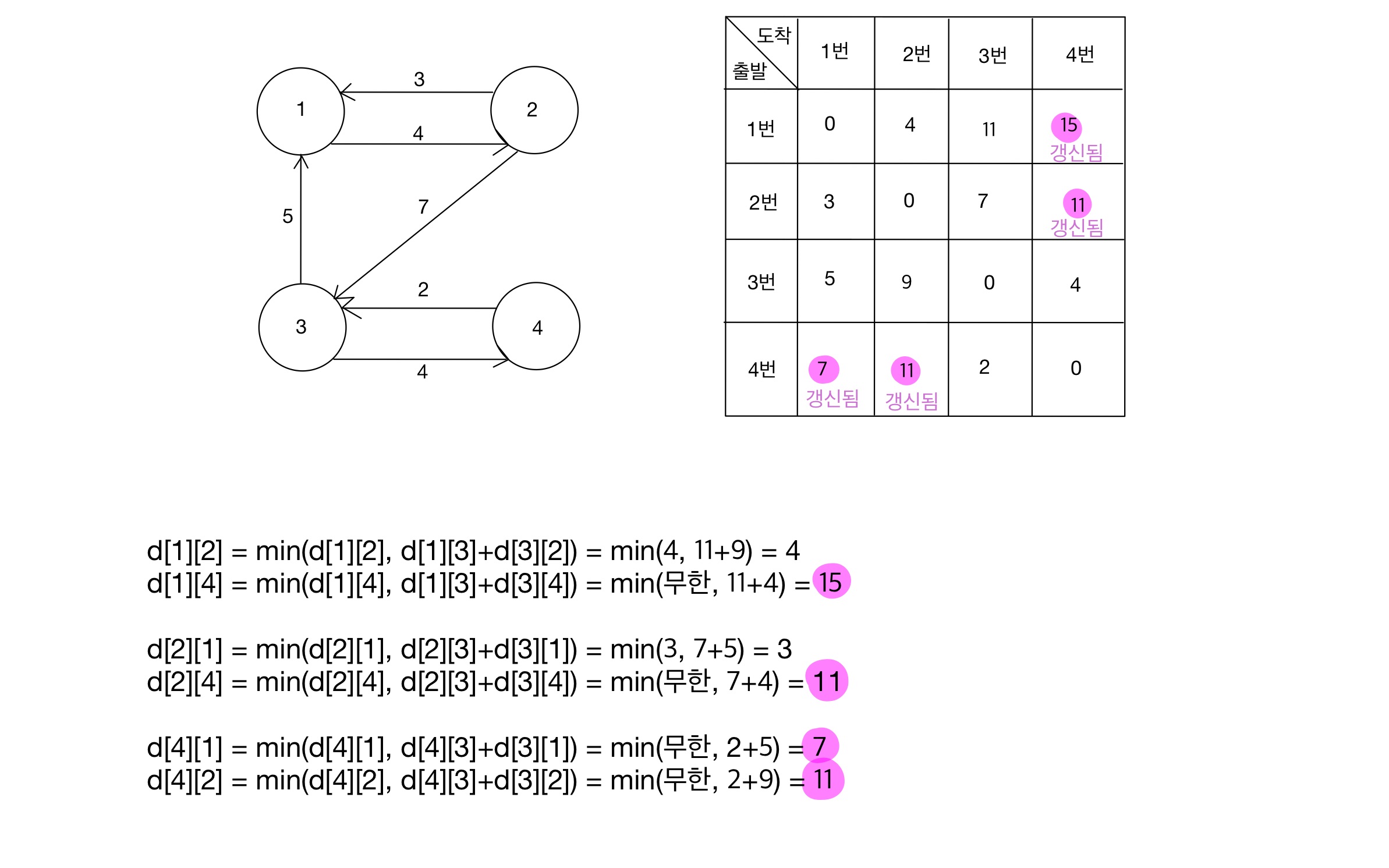
현재 확인 중인 노드(K)가 3일 때, ‘3을 제외한 나머지 노드들에 대해 가능한 모든 경로’에 점화식을 적용한다.

Step 05 (K = 4)

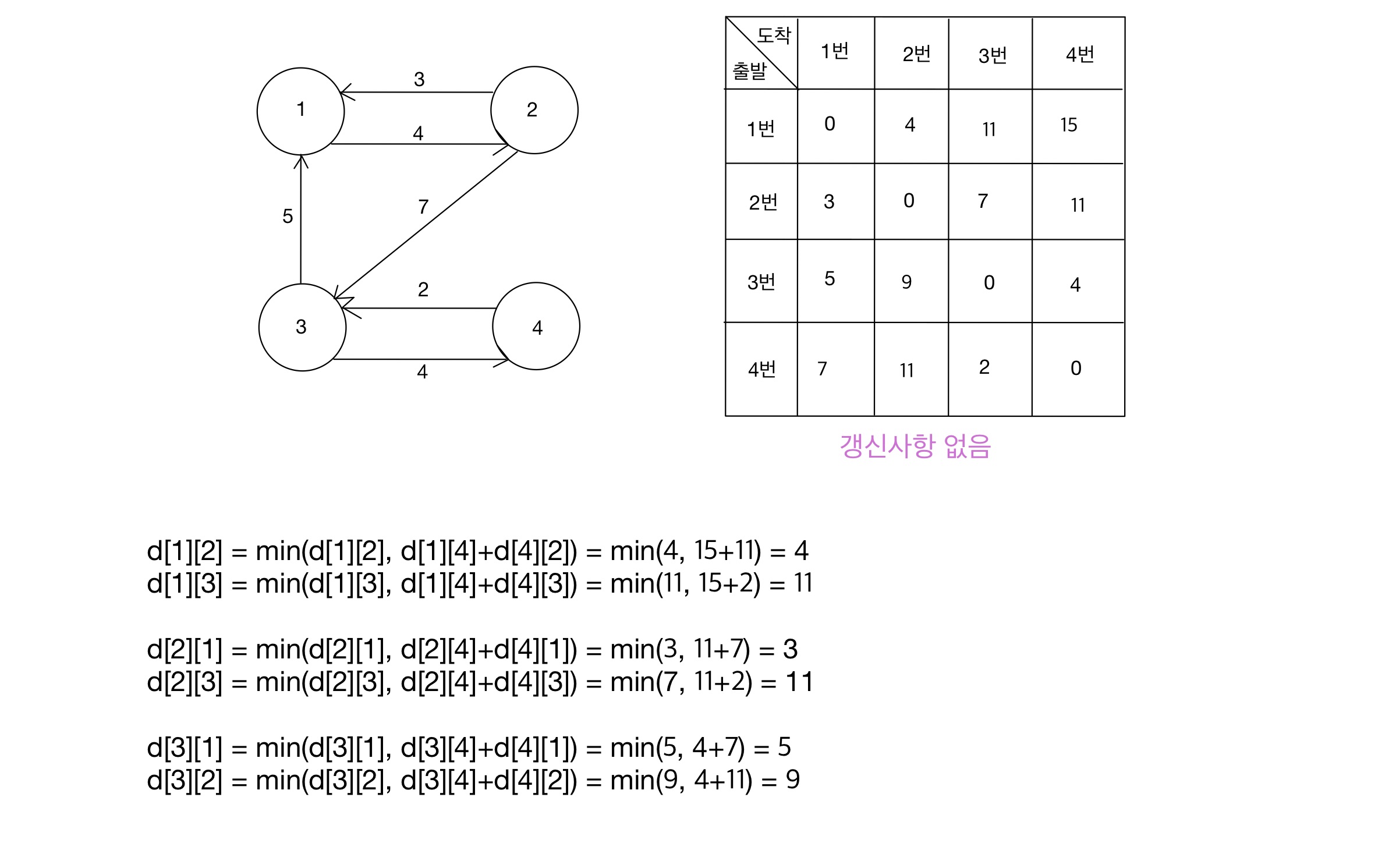
현재 확인 중인 노드(K)가 4일 때, ‘4을 제외한 나머지 노드들에 대해 가능한 모든 경로’에 점화식을 적용한다.

소스코드

플로이드 워셜 알고리즘

package shortestpath;



import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;

public class 플로이드_워셜 {
  static final int INF = (int) 1e9; //무한을 의미하는 값으로 10억을 설정
  static int sizeOfNode;
  static int sizeOfEdge;
  static int[][] graph = new int[501][501]; //그래프


  /**
   * 실행 메서드
   */
  public static void execute() throws Exception {
    BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
    sizeOfNode = Integer.parseInt(bf.readLine());
    sizeOfEdge = Integer.parseInt(bf.readLine());

    //그래프를 무한으로 초기화
    for (int i = 0; i < graph.length; i++) {
      Arrays.fill(graph[i], INF);
    }

    //자기자신으로 가는 최소 거리는 0이므로 0으로 초기화
    for (int i = 1; i < graph.length; i++) {
      for (int u = 1; u < graph[i].length; u++) {
        if (i == u) graph[i][u] = 0;
      }
    }

    //입력받은 간선 정보로 그래프의 나머지 부분 초기화
    for (int i = 0; i < sizeOfEdge; i++) {
      String s = bf.readLine();
      StringTokenizer st = new StringTokenizer(s);
      int fromNode = Integer.parseInt(st.nextToken());
      int toNode = Integer.parseInt(st.nextToken());
      int distance = Integer.parseInt(st.nextToken());
      graph[fromNode][toNode] = distance;
    }

//    solution1();
    solution2();

    for (int i = 1; i <= sizeOfNode; i++) {
      for (int u = 1; u <= sizeOfNode; u++) {
        if (graph[i][u] >= INF) {
          System.out.print("INFINITE");
        } else {
          System.out.print(graph[i][u] + " ");
        }
      }
      System.out.println();
    }
  }

  /**
   * 플로이드 워셜 수행 메서드
   */
  private static void solution1() {

    for (int k = 1; k <= sizeOfNode; k++) {
      for (int a = 1; a <= sizeOfNode; a++) {
        if (a == k) continue; //k를 제외한 나머지에서 선택해야하므로

        for (int b = 1; b <= sizeOfNode; b++) {
          if (b == k) continue; //k를 제외한 나머지에서 선택해야하므로
          if (b == a) continue; //k를 제외한 노드 중, 같은 노드끼리인 경우는 생략 (거리=0)
          graph[a][b] = Math.min(graph[a][b], graph[a][k]+graph[k][b]);
        } //for문 종료

      } //for문 종료
    } //for문 종료
  }

  /**
   * 플로이드 워셜 수행 메서드 (쓸데없는 if문 제거 ver.)
   */
  private static void solution2() {
    for (int k = 1; k <= sizeOfNode; k++) {
      for (int a = 1; a <= sizeOfNode; a++) {
        for (int b = 1; b <= sizeOfNode; b++) {
          graph[a][b] = Math.min(graph[a][b], graph[a][k]+graph[k][b]);
        }//for문 종료
      }//for문 종료
    }//for문 종료

  }

}

solution1 메서드와 solution2 메서드의 차이점
- solution1 메서드는 위 문서 내용을 그대로 코드화시켰다.
- solution2 메서드는 로직상 삭제해도 영향이 없는 코드를 삭제했다.
  - 플로이드 워셜 알고리즘에선 원래, 현재 수행 중인 노드(k)를 제외한 나머지 노드들 중에서 점화식을 계산해야 한다.
  - 하지만 노드 k 를 포함하여 점화식 계산을 수행하더라도, 최소값을 구하는 min() 메서드가 존재하기에 문제가 없다.
  - 따라서 solution2 메서드에선 필요없는 코드 (if문 3개)를 제거했다.

나동빈, 『이것이 코딩 테스트다』

본 게시글은 위 교재를 기반으로 정리한 글입니다.