자료형 & 추상 자료형

추상 자료형

추상화란?

• 어떤 시스템의 간략화 된 기술 또는 명세
• 정보은닉

추상 자료형이란?

• ADT : Abstract Data Type
• 데이터나 연산이 무엇인가를 정의
• 데이터나 연산을 어떻게 구현할 것인지는 정의하지 않음

자료형 vs 추상 자료형

자료형이란?

• 데이터의 집합 + 연산의 집합

자료형 예시

데이터	{ …, -2, -1, 0, 1, 2, … }
연산	+, -, *, /, %

추상 자료형이란?

• 데이터 : 집합 개념
• 연산의 정의 : 연산의 이름, 매개변수, 연산의 결과, 연산이 수행하는 기능 등을 기술

즉, 연산은 함수와 유사하다.

추상 자료형 예시

	<자연수 ADT="">
데이터	1에서 시작하여 INT_MAX까지의 순서화된 정수의 부분 범위
연산	add(x, y) : x+y가 INT_MAX보다 작으면 x+y 반환 distance(x, y) : x가 y보다 크면 x-y 반환, x가 y보다 작으면 y-x 반환

추상 자료형 & 자료구조

추상 자료형과 자료구조의 관계

자료구조

자료구조는 추상 자료형을 프로그래밍 언어로 구현한 것

추상 자료형 구현

C언어에서의 추상 자료형

• 데이터 : 구조체
• 연산 : 함수

실행 시간 측정법

함수

사용 함수

#include <time.h>
clock()

<측정시간을 현실시간으로="" 변환="" 공식=""> > (double) (끝시각 - 시작시각) / CLOCKS_PER_SEC
### 반환값 - clock_t 타입 - 호출되었을 때의 시스템 시각 ### 예시 코드 ```c #include #include #include int main(void) { clock_t start, end; double result; start = clock(); //시간을 측정하려는 코드... end = clock(); //시간계산 result = (double) (end-start)/ CLOCKS_PER_SEC; } ```


# 알고리즘 성능 분석 ## 알고리즘 복잡도 분석 ### 복잡도 분석 종류 - **시간 복잡도 분석** : 알고리즘의 수행 시간 분석 - **공간 복잡도 분석** : 수행시 필요로 하는 메모리 공간 분석
## 시간 복잡도 ### 연산 고려 조건 - 산술 연산 - 대입 연산 - 비교 연산 - 이동 연산 > **보통 반복 루프 제어 연산은 고려X** ### 특징 - 입력 개수 n에 영향 받음 - 시간복잡도 함수 ⇒ T(n) ### 계산 예시 ```c #include #include int main(void) { int n; //n은 입력의 크기 int sum = 0; // 1 int i = 0; // 1 for(i=0; i<n; i++) { // 루프 제어는 고려X sum += i; // 더하기 연산 1번 * n sum--; // 빼기 연산 1번 * n } } ``` > **따라서 T(n) = 2n + 2**


# 빅오 표기법 ## 설명 ### 정의 두 개의 함수 f(n)과 g(n)이 주어졌을 때, 모든 n≥n0에 대하여 \|f(n)\| ≤ c\|g(n)\|을 만족하는 2개의 상수 c, n0이 존재하면 f(n) = O(g(n))이다. ### 특징 빅오는 상한이다. ### 계산 방법 차수가 가장 큰 항 이외의 항 무시, 또한 해당 항의 계수도 무시 ### 예시 "T(n) = 2n^2 + 5n +10"일때 ⇒ O(n^2)
## 빅오 표기법의 종류 ### 종류 - **O(1)** : 상수형 - **O(logn)** : 로그형, 문제가 절반씩 연속적으로 줄어드는 경우 ```c for(int i=1; i<n; i*=2) { //do } ``` - **O(n)** : 선형 - **O(nlogn)** : 로그선형 - **O(n^2)** : 2차형 - **O(n^k)** : k차형 - **O(2^n)** : 지수형 - **O(n!)** : 팩토리얼형 ### 빅오 표기법의 복잡도 순 O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^k) < O(2^n) < O(n!)

# 빅오메가 표기법 ## 배경 ### 빅오의 상한 문제 - 빅오는 상한이기 때문에 O(n)을 만족한다면, O(n^2) 등도 모두 만족함 ## 설명 ### 정의 > **두 개의 함수 f(n)과 g(n)이 주어졌을 때, 모든 n≥n0에 대하여 |f(n)| ≥ c|g(n)|을 만족하는 2개의 상수 c, n0이 존재하면 f(n) = Ω(g(n))이다.** ### 특징 - 빅오메가는 하한이다.

# 빅세타 표기법 ## 설명 ### 정의 > **두 개의 함수 f(n)과 g(n)이 주어졌을 때, 모든 n≥n0에 대하여 c1|g(n)| ≤ |f(n)| ≤ c2|g(n)|을 만족하는 3개의 상수 c1, c2, n0이 존재하면 f(n) = θ(g(n))이다.** ### 특징 - O() == Ω()


# 1차원 배열 ## 설명 ### 배열의 특징 - 직접 접근 방식 - 항목 접근 시간 복잡도 ⇒ O(1) | <링크드 리스트(연결 리스트)> | |------------------------------| |순사접근방식 (첫 요소부터 하나씩 찾아감)| |항목 접근 시간 복잡도 ⇒ O(n)|
### 배열의 초기화 `자료형 변수명[크기n] = { 요소1, 요소2, ..., 요소n }` <예시> ```c int nums[5] = { 1, 2, 3 }; ``` >배열의 크기보다 적은 수의 요소로 초기화 ⇒ 나머지 공간을 0으로 채움

## 문자열 : 특별한 1차원 배열 ### 선언방법 `char 변수명[크기] = "문자열";` ```c #include int main(void) { char name[10] = "홍길동"; } ```
### 문자열 복사 함수 ```c #include strcpy(복사, 원본); ``` - 문자열은 대입연산자(=) 사용 불가 - 항상 가장 마지막 요소에는 문자열의 끝을 알리는 '\0'이 들어감  ```c #include int main(void) { char name[10] = "홍길동"; char copy[10]; strcpy(copy, name); } ```

### 문자열 비교 함수 ```c #include strcmp(문자열1, 문자열2) ```


# 2차원 배열 ## 설명 ### 선언 방법 `데이터타입 배열이름[행의개수][열의개수] int nums[5][3];` ### 초기화 방법 ```c int nums[3][4] = { {1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12} } ``` ### 특징 : row-oriented 같은 행끼리 붙여서 메모리에 저장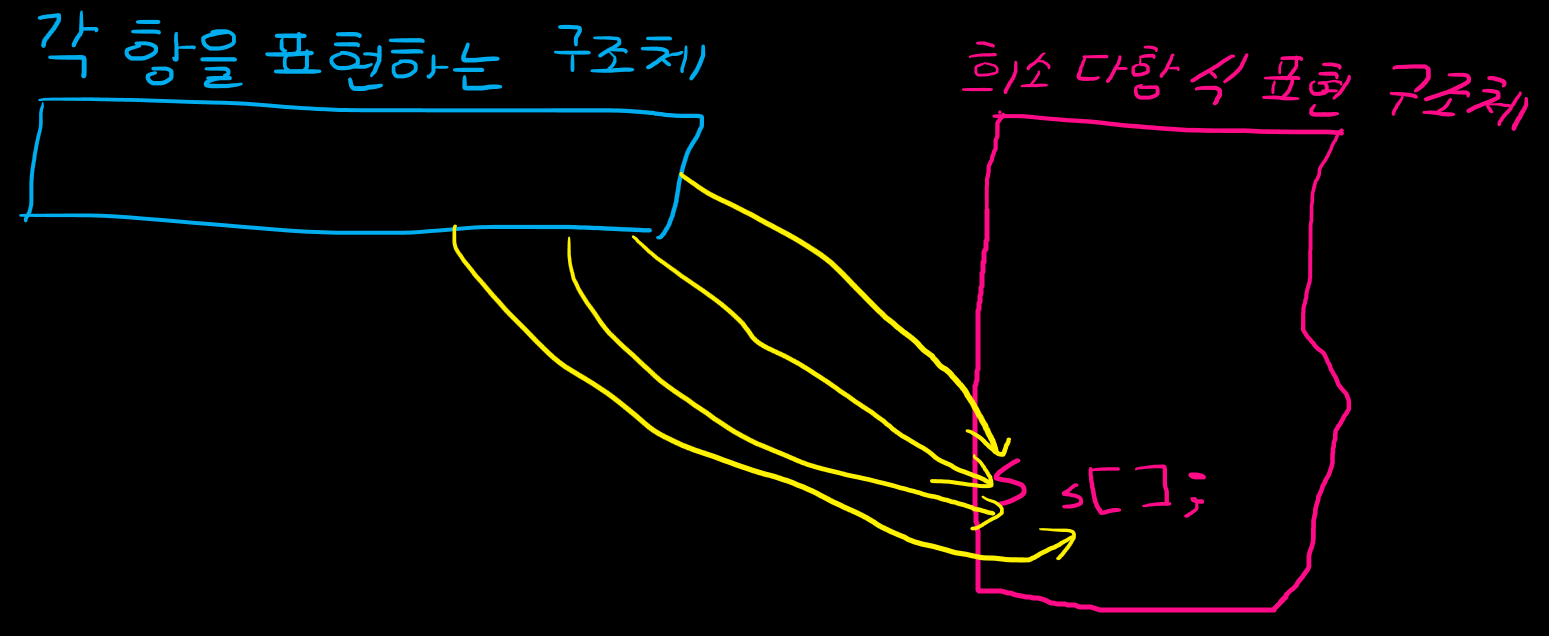 


# 파라미터 전달 방식 ## 변수의 전달 ### 특징 - 값 자체를 복사하여 전달한다. ### 예시 ```c #include #include void change(int a, int b) { b = a; } int main(void) { int A = 10; int B = 5; change(A, B); //결과 //A == 10, B == 5 //값 자체를 복사하기 때문에 A,B 변화 X } ```

## 배열의 전달 ### 특징 - 주소를 복사하여 전달한다. - 함수로 배열(주소)을 전달할 때, 길이도 같이 전달해야 한다. (보통 배열의 길이까지 매개변수로 받는다.)


# 구조체 ## 설명 ### 구조체란? - 데이터타입이 각각 요소마다 다른 배열 ## 사용 방법 1 : struct ### 정의 방법 ```c #include struct 구조체이름 { 데이터타입a 요소이름a; 데이터타입b 요소이름b; 데이터타입c 요소이름c; }; ``` ### 선언 방법 ```c #include struct 구조체이름 { 데이터타입a 요소이름a; 데이터타입b 요소이름b; 데이터타입c 요소이름c; }; int main(void) { struct 구조체이름 변수명; } ``` ### 초기화 방법 ```c #include struct 구조체이름 { 데이터타입a 요소이름a; 데이터타입b 요소이름b; 데이터타입c 요소이름c; }; int main(void) { struct 구조체이름 변수명 = { 첫번째요소값, 두번째요소값, 세번째요소값 }; } ```
## 사용 방법 2 : typedef ### 정의 방법 ```c #include typedef struct 구조체이름 { 데이터타입a 요소이름a; 데이터타입b 요소이름b; 데이터타입c 요소이름c; } 별칭; ``` > typedef로 별칭까지 설정시, 구조체이름은 생략가능 ### 선언 방법 ```c #include typedef struct 구조체이름 { 데이터타입a 요소이름a; 데이터타입b 요소이름b; 데이터타입c 요소이름c; } 별칭; int main(void) { 별칭 변수명; } ``` ### 초기화 방법 ```c #include typedef struct 구조체이름 { 데이터타입a 요소이름a; 데이터타입b 요소이름b; 데이터타입c 요소이름c; } 별칭; int main(void) { 별칭 변수명 = { 첫번째요소값, 두번째요소값, 세번째요소값 }; } ```
## 멤버 접근 ### 항목 연산자 - .(마침표) 사용 - 구조체의 멤버변수가 문자열타입일 때, 대입 연산자로 값 할당 불가능 ⇒ strcpy 함수 사용 ### 예시 ```c #include struct person { int age; char name[10]; }; int main(void) { struct person me; me.age = 24; //me.name = "홍길동"; => 불가능!!!!!! strcpy(me.name, "홍길동"); } ```
## 구조체 복사 ### 대입 연산자 - 대입 연산자 사용시 깊은 복사를 함 ### 예시 ```c #include #include struct person { int age; char name[10]; }; int main(void) { struct person me; struct person you; me.age = 24; strcpy(me.name, "홍길동"); you = me; strcpy(you.name, "김영미"); //결과 //me.name == "홍길동", me.age == 24 //you.name == "김영미", you.age == 24 } ```


# 배열과 구조체 응용 : 다항식 ## 설명 ### 다항식 형태 - p(x) = a_nx^n + a_{n-1}x^{n-1} +... + a_1x + a_0 ### 다항식의 차수 - 다항식의 차수(degree) : 다항식에서 가장 큰 차수

## 다항식의 배열 표현 : 다항식의 왼쪽부터 계수 저장 ### 방법 다항식의 왼쪽 항부터 계수를 배열에 저장한다. - 항의 계수 : 배열에 저장 - 항의 차수 : 배열의 인덱스 > '다항식의 차수' - '배열 요소 중 해당요소의 인덱스' = 차수 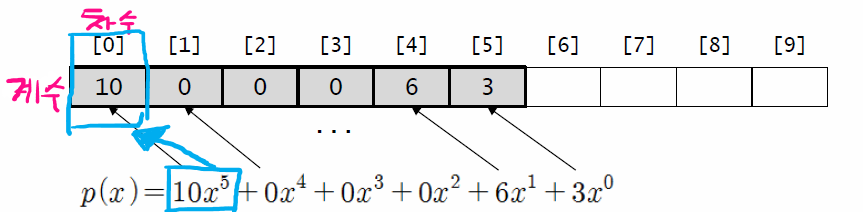 ### 예시 다항식 - p(x) = 10x^{5}+6x+3 ### 다항식 변환 - 다항식을 1차원 배열로 표현하기 위해 변환한다. - p(x) = 10x^{5}+6x+3 = 10x^{5}+0x^{4}+0x^{3}+0x^{2}+6x+3x^0 ### 예시 코드 ```c #include //다항식 구조체 정의 #define MAX_DEGREE 101 //구조체의 최대 차수 = 100 설정 typedef struct { int degree; //다항식의 차수 int coef[MAX_DEGREE]; //계수 저장하는 배열 } Poly; int main() { //다항식 : 10x^5 + 6x + 3 //다항식 구조체 표현 Poly p; p.degree = 5; //다항식의 차수 p.coef[0] = 10; //계수 설정 p.coef[1] = 0; p.coef[2] = 0; p.coef[3] = 0; p.coef[4] = 6; p.coef[5] = 3; } ```

## 다항식의 배열 표현 : 다항식의 오른쪽부터 계수 저장 ### 방법 다항식의 오른쪽 항부터 계수를 배열에 저장한다. - 항의 계수 : 배열에 저장 - 항의 차수 : 배열의 인덱스 > '배열 요소 중 해당요소의 인덱스' = 차수 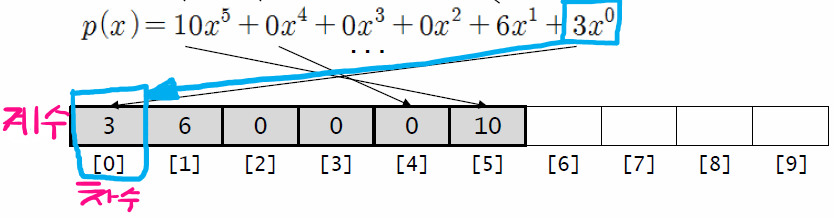 ### 예시 다항식 - p(x) = 10x^{5}+6x+3 ### 다항식 변환 - 다항식을 1차원 배열로 표현하기 위해 변환한다. > p(x) = 10x^{5}+6x+3 = 10x^{5}+0x^{4}+0x^{3}+0x^{2}+6x+3x^0 ### 예시 코드 ```c #include //다항식 구조체 정의 #define MAX_DEGREE 101 //구조체의 최대 차수 = 100 설정 typedef struct { int degree; //다항식의 차수 int coef[MAX_DEGREE]; //계수 저장하는 배열 } Poly; int main() { //다항식 : 10x^5 + 6x + 3 //다항식 구조체 표현 Poly p; p.degree = 5; //다항식의 차수 p.coef[5] = 10; //계수 설정 p.coef[4] = 0; p.coef[3] = 0; p.coef[2] = 0; p.coef[1] = 6; p.coef[0] = 3; } ```

## 다항식 구현 : 방법 1 ### 방법 1 vs 방법 2 - 다항식의 차수 - 배열의 인덱스 = 각 항의 차수 ⇒ 방법 1 - 배열의 인덱스 = 각 항의 차수 ⇒ 방법 2 ### 코드 ```c #include //다항식 구조체 정의 #define MAX_DEGREE 101 typedef struct { int degree; float coef[MAX_DEGREE]; } Poly; //다항식 입력 함수 Poly setPoly() { Poly p; printf("다항식의 차수를 입력하세요 : "); scanf("%d", &p.degree); int i; printf("다항식의 계수들을 차례대로 입력해주세요."); for(i=0; i<=p.degree; i++) { scanf("%f", &p.coef[i]); } return p; } //다항식 출력 함수 void printPoly(Poly p) { int i; for(i=0; i<p.degree; i++) { // "p.degree - i"가 차수 printf("%.1fx^%d + ", p.coef[i], p.degree - i); } printf("%.1f", p.coef[p.degree]); } int main() { Poly p = setPoly(); printPoly(p); } ```

## 다항식 구현 : 방법 2 ### 방법 1 vs 방법 2 - 다항식의 차수 - 배열의 인덱스 = 각 항의 차수 ⇒ 방법 1 - 배열의 인덱스 = 각 항의 차수 ⇒ 방법 2 ### 코드 ```c #include //다항식 구조체 정의 #define MAX_DEGREE 101 typedef struct { int degree; float coef[MAX_DEGREE]; } Poly; //다항식 입력 함수 Poly setPoly() { Poly p; printf("다항식의 차수를 입력하세요 : "); scanf("%d", &p.degree); int i; printf("다항식의 계수들을 차례대로 입력해주세요."); for(i=p.degree; i>=0; i--) { scanf("%f", &p.coef[i]); } return p; } //다항식 출력 함수 void printPoly(Poly p) { int i; for(i=p.degree; i>0; i--) { // "i"가 차수 printf("%.1fx^%d + ", p.coef[i], i); } printf("%.1f", p.coef[0]); } int main() { Poly p = setPoly(); printPoly(p); } ```

## 희소 다항식의 표현 ### 희소 다항식이란? 대부분 항의 계수가 0인 다항식 > 10x^{100} + 7 ### 기존 방식의 문제점 희소 다항식을 1차원 배열로 표현한다면, 메모리 낭비가 심해짐 ### 해결법 "각 항의 차수와 계수를 담는 구조체"를 멤버로 갖는 구조체 이용  ### 예시 코드 ```c #include //하나의 항을 표현하는 구조체 typedef struct { int degree; //해당 항의 차수 float coef; //해당 항의 계수 } Hang; //희소 다항식을 표현하는 구조체 #define MAX_HANG 100 //최대로 가질 수 있는 항의 개수 typedef struct { int nHang; //계수가 0이 아닌 항의 개수 Hang h[MAX_HANG]; //각 항을 담는 배열 } Poly; ```

---

• 성결대학교 컴퓨터 공학과 박미옥 교수님 (2021)
• 최영규, 『두근두근 자료구조』

본 게시글은 위 강의 및 교재를 기반으로 정리한 글입니다.