스택
개요
스택의 특징
- 후입선출(LIFO)
구현 방법
- 1차원 배열
- 연결리스트
스택의 구조
- 스택 상단 : top
- 스택 하단 : 불필요
- 요소
- 삽입 연산
- 삭제 연산
상태
- 공백 상태 : 요소가 하나도 없는 상태
- 포화 상태 : 요소가 가득 차있는 상태
스택 추상 자료형 (ADT : Abstract Data Type)
객체
무엇이든 가능하다.
연산
- 새로운 항목을 스택에 삽입
- 하나의 항목 꺼내기
- 스택이 비어있는지 살핌
추상 자료형 정의
- init() : 스택 초기화
- is_empty() : 스택이 비어있으면 True, 아니면 False 반환
- is_full() : 스택이 꽉차면 True, 아니면 False 반환
- size() : 스택 내의 모든 요소들의 개수 반환
- push(x) : 주어진 요소 x를 스택의 맨 위에 추가
- pop() : 스택 맨 위에 있는 요소를 삭제하고 반환
- peek() : 스택 맨 위에 있는 요소를 삭제하지 않고 반환
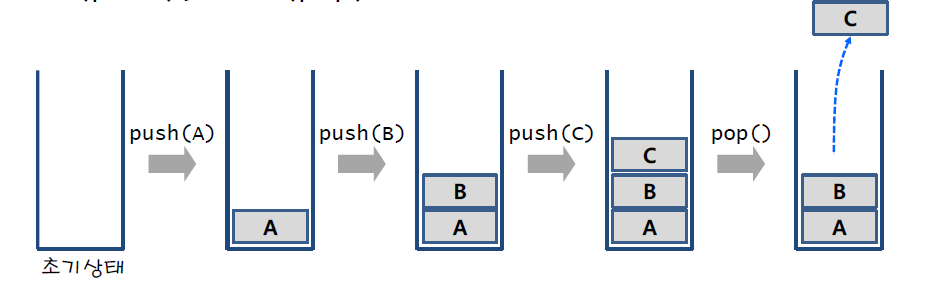
스택의 연산
삽입(push) & 삭제(pop)
- is_empty() : 스택이 공백상태인지 검사
- is_full() : 스택이 포화상태인지 검사
- peek() : 요소를 스택에서 삭제하지 않고 보기만 하는 연산
스택 활용 분야
개념
자료의 출력순서가 입력순서의 역순으로 이루어져야 할 경우에 사용
분야
- 편집기의 되돌리기
- 함수호출 스택
- Program Counter (PC)
- 다음에 실행할 명령어의 주소를 저장
스택 구현 방법
배열 vs 연결리스트
- 배열 : 가장 간단하게 구현, 고정된 크기
- 연결 리스트 : 복잡한 코드, 유연한 크기
배열을 이용한 스택 구현
구성 원리
1차원 배열을 활용하여 구현한다.
- top : 가장 최근에 입력된 자료를 가르키는 변수
- stack[0] ~ stack[top] : 먼저 들어온 순으로 저장
- 공백상태 : top == -1
- 포화상태 : top == MAX_STACK_SIZE-1
스택 연산 : is_empty()
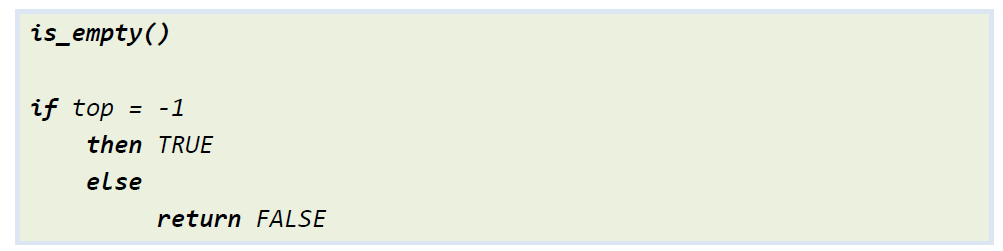
스택 연산 : is_full()
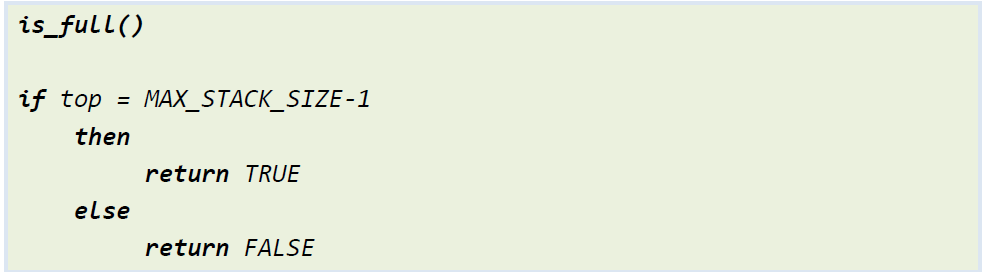
스택 연산 : init()
- 초기화
- 스택을 공백상태로 만드는 것
- top == -1

스택 연산 : size()
- 요소의 개수
- top + 1

스택 연산 : push()
- 요소 추가
- 새로운 항목은 스택의 맨 위에 올라가야 함
- top을 하나 증가
- 스택이 포화상태인지 체크

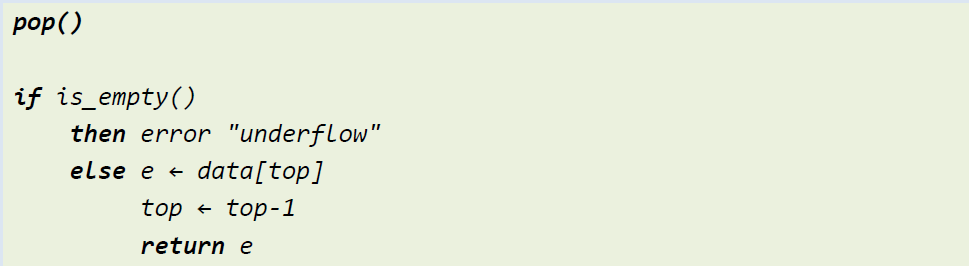
스택 연산 : pop()
- 요소를 꺼내서 반환
- 공백 상태인지 체크
- top이 가르키는 값 반환
- top이 하나 감소
int형 스택 자료형 선언
스택의 항목의 자료형을 Element이라고 칭하자.
(요소의 데이터타입 선언)

스택 구현 : int형 요소의 스택
스택 배열 선언
//최대 크기 선언
#define MAX_STACK_SIZE 100
//요소 타입 선언 (int형 요소)
typedef int Element;
//스택 배열 선언
Element stack[];
//top 선언
int top;
스택 주요 함수 선언
//init 함수
void init_stack() {
top = -1;
}
//size 함수
int size() {
return top+1;
}
//is_empty 함수
int is_empty() {
return (top == -1);
}
//is_full 함수
int is_full() {
return (top == MAX_STACK_SIZE - 1);
}
//push 함수
void push(Element e) {
if(is_full()) {
printf("스택포화에러");
} else {
stack[++top] = e;
}
}
//pop 함수
Element pop() {
if(is_empty) {
printf("빈 스택");
}
return stack[top--];
}
//peek 함수
Element peek() {
if(is_empty) {
printf("빈스택");
}
return stack[top];
}
//print_stack 함수
void print_stack(char msg[]) {
int i;
printf("%s[%2d] = ", msg, size());
for(i=0; i<size(); i++) {
printf("%2d ", stack[i]);
}
printf("\n");
}
error함수
void error(char msg[]) {
printf("%s\n", msg);
exit(1);
}
main
int main() {
int i;
init_stack();
for(i=1; i<40; i++) {
printf("push i : %d\n", i);
push(i);
}
print_stack("스택 push 9회");
printf("--------------pop---------------\n");
printf("pop() = %d\n", pop());
printf("pop() = %d\n", pop());
printf("pop() = %d\n", pop());
printf("%d", stack[1]);
}
- 성결대학교 컴퓨터 공학과 박미옥 교수님 (2021)
- 최영규, 『두근두근 자료구조』
