리스트

개요

리스트란?

리스트 == 선형 리스트
순서를 가진 항목들의 모임

리스트의 특징

임의의 위치에서도 삽입, 삭제가 가능함

리스트 ADT

데이터

같은 타입 요소들의 순서있는 모임

연산

init()
- 리스트를 초기화한다.
insert( pos, item )
- pos 위치에 새로운 요소 item을 삽입
delete(pos)
- pos 위치에 있는 요소를 삭제
get_entry(pos)
- pos 위치에 있는 요소를 반환
is_empty()
- 리스트가 비어있는지 검사
is_full()
- 리스트가 가득 차있는지 검사
find(item)
- 리스트의 요소 item의 인덱스 반환
replace(pos, item)
- pos 위치를 새로운 요소 item으로 바꿈
size()
- 리스트안의 요소의 개수 반환

리스트 구현 개요

구현 방법의 종류

배열 활용시
- 구현이 간단
- 삽입, 삭제시 오버헤드 발생
- 원소들을 연산마다 이동을 시켜야함
  
  따라서, 항목의 개수가 제한됨
연결 리스트 활용시
- 구현 복잡
- 삽입, 삭제 용이
- 크기 제한X

구현 (by. 배열)

특징

중간에 비어 있는 항목 없어야 함

공백상태

length == 0 인지 검사

포화상태

length == MAX_LIST_SIZE 인지 검사

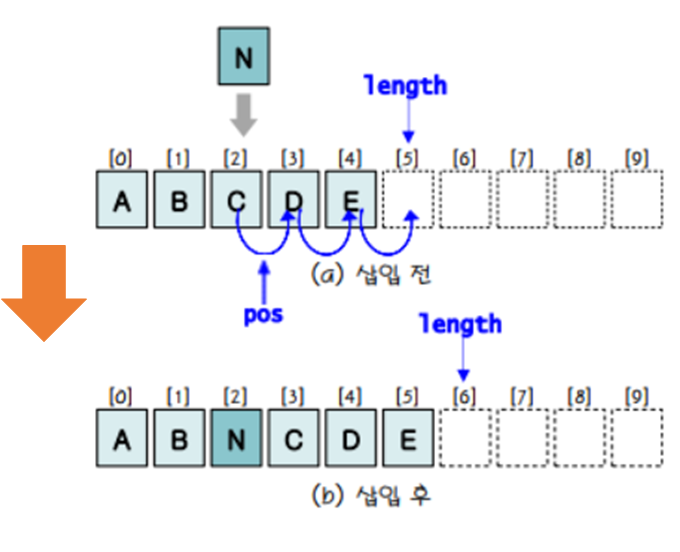
삽입 연산

삽입 위치 다음의 모든 항목들을 뒤로 한 칸씩 이동시킴
가장 뒤에 있는 요소부터 뒤로 이동시킴

삽입연산by배열

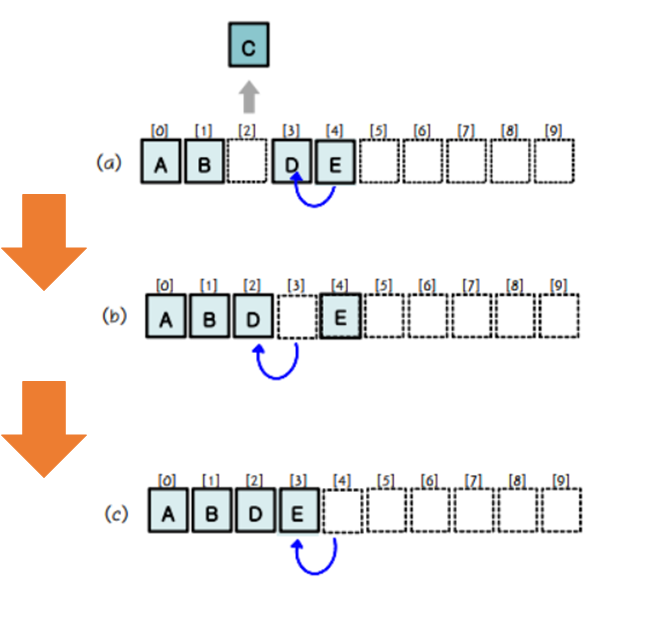
삭제 연산

삭제 위치 다음의 항목들을 이동해야 함
삭제할 위치의 뒷요소부터 앞으로 이동시킴
시간복잡도: O(n)

매우 비효율적임

삭제연산by배열

초기변수설정

#define MAX_LIST_SIZE 100
typedef int Element;
Element list[MAX_LIST_SIZE];
int length = 0;

error(char *msg)

void error(char *msg) {
	printf("%s", msg);
	exit(1);
}

init_list()

void init_list() {
	length = 0;
}

size()

int size() {
	return length;
}

get_entry(int index)

Element get_entry(int index) {
	return list[index];
}

replace(int index, Element e)

void replace(int index, Element e) {
	list[index] = e;
}

clear_list()

void clear_list() {
	length = 0;
}

is_empty()

int is_empty() {
	return length==0;
}

is_full()

int is_full() {
	return length==MAX_LIST_SIZE;
}

insert( int pos, Element e )

void insert( int pos, Element e ) {
	int i;
	
	if( is_full()==0 && pos>=0 && pos<=length ) { // 리스트가 가득 차있지않고, 삽입인덱스가 음수가 아니고, 삽입위치가 length이내일 때 
		for( i=length; i>pos; i-- ) { // 가장 마지막 요소부터 삽입될 인덱스의 뒷요소까지 한칸씩 뒤로 민다.
			list[i] = list[i-1];
		}
		list[pos] = e;
		length++;
	}
}

delete(int pos)

void delete( int pos ) {
	int i;
	
	if( is_empty()==0 && 0<=pos && pos<length ) { // 리스트가 비어있지 않고, 삭제할 요소의 인덱스가 음수가 아니고, length 이내일 때
		for(i=pos+1; i<length; i++) { //삭제할 요소의 뒷요소부터 끝까지 앞으로 이동시킴
			list[i-1] = list[i];
		}
		length--;
	}
}

find( Element e )

Element find( Element e ) {
	int i;
	
	for(i=0; i<length; i++) {
		if(list[i]==e) {
			return i; //탐색성공, 인덱스 반환
		}
	}
	return -1; //탐색 실패
}

전체 구현

#include <stdio.h>
#define MAX_LIST_SIZE 100
typedef int Element;
Element list[MAX_LIST_SIZE];
int length = 0;

void error(char *msg) {
	printf("%s", msg);
	exit(1);
}

void init_list() {
	length = 0;
}

int size() {
	return length;
}

Element get_entry(int index) {
	return list[index];
}

void replace(int index, Element e) {
	list[index] = e;
}

void clear_list() {
	length = 0;
}

int is_empty() {
	return length==0;
}

int is_full() {
	return length==MAX_LIST_SIZE;
}

void insert( int pos, Element e ) {
	int i;
	
	if( is_full()==0 && pos>=0 && pos<=length ) { // 리스트가 가득 차있지않고, 삽입인덱스가 음수가 아니고, 삽입위치가 length이내일 때 
		for( i=length; i>pos; i-- ) { // 가장 마지막 요소부터 삽입될 인덱스의 뒷요소까지 한칸씩 뒤로 민다.
			list[i] = list[i-1];
		}
		list[pos] = e;
		length++;
	}
}

void delete( int pos ) {
	int i;
	
	if( is_empty()==0 && 0<=pos && pos<length ) { // 리스트가 비어있지 않고, 삭제할 요소의 인덱스가 음수가 아니고, length 이내일 때
		for(i=pos+1; i<length; i++) { //삭제할 요소의 뒷요소부터 끝까지 앞으로 이동시킴
			list[i-1] = list[i];
		}
		length--;
	}
}

Element find( Element e ) {
	int i;
	
	for(i=0; i<length; i++) {
		if(list[i]==e) {
			return i; //탐색성공, 인덱스 반환
		}
	}
	return -1; //탐색 실패
}

int main() {
	int i;
	init_list();
	insert(0, 20); insert(1, 15); insert(2, 20); insert(2, 30); insert(1, 40); 
	for(i=0; i<size(); i++) {
		printf("%d, ", get_entry(i));
	}
	
	delete(2); delete(0); delete(1); 
	printf("\n");
	for(i=0; i<size(); i++) {
		printf("%d, ", get_entry(i));
	}
	
}

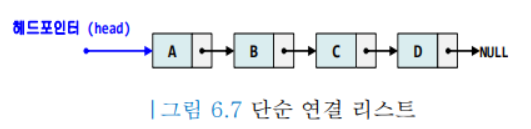
구현 (by. 연결리스트)

특징

단순 연결리스트 사용
링크 필드를 이용하여 연결
마지막 노드의 링크 값: NULL
크기 제한X

연결리스트 특징

공백상태

head == NULL 인지 검사

포화상태

연결리스트는 끝이 없기 때문에, 의미가 없다.

항목 참조(get_entry) 연산

리스트에서 pos번째 노드를 찾아 반환
시작노드부터 하나씩 따라가며 pos번째 노드 찾음
시간복잡도: O(n)

삽입 연산

첫번째 노드로 삽입할 경우
1. ‘추가할 노드의 link 필드 값’를 ‘헤드 포인터의 값’으로 취함
2. ‘헤드 포인터의 값’를 ‘추가할 노드의 주소값’으로 취함

중간 노드로 삽입할 경우
1. ‘추가할 노드의 link 필드 값’을 ‘추가할 노드가 들어갈 인덱스의 앞 노드의 link 필드 값’으로 취함
2. ‘추가할 노드가 들어갈 인덱스의 앞 노드의 link 필드 값’을 ‘추가할 노드의 주소값’으로 취함
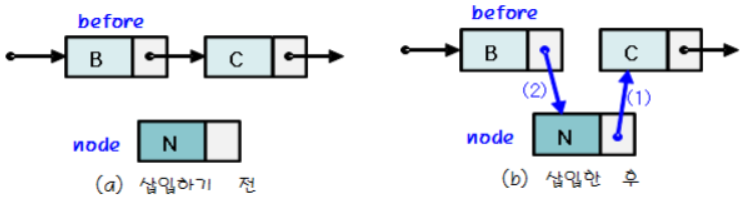
즉, 추가될 위치의 앞 노드를 알아야 삽입이 가능함

**<위 두="" 경우의="" 처리방법이="" 다른="" 이유="">** 첫번째 노드로 삽입될 땐, 추가될 위치의 앞노드가 존재하지 않기 때문이다.

시간복잡도: O(1)

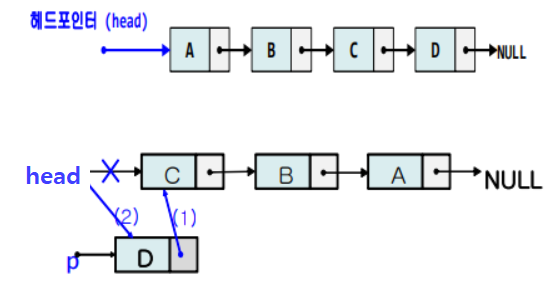
삭제 연산

첫번째 노드를 삭제할 경우
1. ‘헤드포인터의 값’을 ‘헤드포인터가 가르키는 노드의 link필드 값’으로 취함
2. free( 헤드포인터가 가르켰었던 노드 )
중간 노드를 삭제할 경우
1. ‘삭제할 노드의 앞 노드의 link필드 값’을 ‘삭제할 노드의 link필드 값’으로 취함
2. free(삭제할 노드)
  
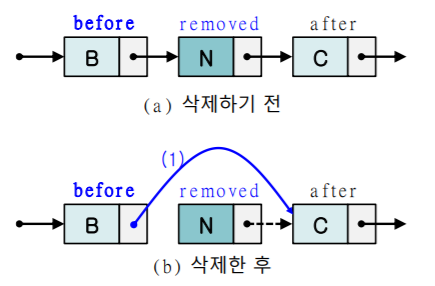
  즉, 추가될 위치의 앞 노드를 알아야 삽입이 가능함

**<위 두="" 경우의="" 처리방법이="" 다른="" 이유="">** 첫번째 노드로 삽입될 땐, 추가될 위치의 앞노드가 존재하지 않기 때문

시간복잡도: O(1)

초기변수 및 구조체

typedef int Element;

//노드
typedef struct LinkedNode {
	Element data; //데이터필드
	struct LinkedNode *link; //링크필드
} Node;

Node *head; //헤드 포인터

error(char *msg)

void error(char *msg) {
	printf("%s", msg);
	exit(1);
}

init_list()

void init_list() {
	head = NULL;
}

size()

int size() {
	int counter = 0;
	Node *n = NULL;
	for(n=head; n!=NULL; n=n->link) {
		counter++;
	}
	return counter;
}

get_entry(int index)

해당 인덱스 번호에 해당하는 노드 반환

Node* get_entry(int index) {
	int i;
	Node *n = head;
	for(i=0; i<index; i++, n=n->link) {
		if(n==NULL) { //끝까지 탐색했을때 (찾으려는 index가 존재하지 않을때)
			return NULL;
		}
	}
	return n;
}

replace(int index, Element e)

void replace(int index, Element e) {
	Node *n = get_entry(index);
	if(n != NULL) {
		n->data = e;
	}
}

clear_list()

void clear_list() {
	while(!is_empty()) {
		delete();
	}
}

is_empty()

int is_empty() {
	return head==NULL;
}

is_full()

포화상태가 존재하지 않기 때문에 구현할 필요가 없다.

insert_next( Node before, Node node ) & insert( int pos, Element e )

void insert_next(Node *before, Node *node) {
	if(node != NULL) {
		node->link = before->link;
		before->link = node;
	}
}

void insert( int pos, Element e ) {
	Node *new_node, *prev;
	new_node = (Node*)malloc(sizeof(Node));
	new_node->data = e;
	new_node->link = NULL;

	if( pos==0 ) { //가장 앞에 노드를 추가할 때

		new_node->link = head;
		head = new_node;

	} else { // 중간에 노드를 추가할 때

		prev = get_entry(pos-1); //추가하려는 인덱스의 앞 노드
		if( prev!=NULL ) {
			insert_next(prev, new_node);
		} else { // 존재하지 않는 인덱스에 추가하려고 할 때
			free(new_node);
		}

	}
}

remove_next(Node *before) & delete(int pos)

Node* remove_next(Node *before) {
	Node *removed = before -> link;
	if( removed != NULL ) {
		before->link = removed->link;
	}
	return removed;
}

void delete( int pos ) {
	Node *prev, *removed;

	if( pos==0 && is_empty()==0 ) { //가장 앞 노드이고, 공백 리스트가 아닐때
		removed = head;
		head = head->link;
		free(removed);
	} else { //중간 노드일 때
		prev = get_entry(pos-1); //삭제할 노드의 앞 노드
		if( prev!=NULL ) {
			removed = remove_next(prev);
			free(removed);
		}
	}
}

find( Element e )

Node* find( Element e ) {
	Node *n;
	for(n=head; n!=NULL; n=n->link) {
		if(n->data == e) {
			return n;
		}
	}
	return NULL; //탐색 실패시
}

전체 구현

#include <stdio.h>

typedef int Element;

//노드
typedef struct LinkedNode {
	Element data; //데이터필드
	struct LinkedNode *link; //링크필드
} Node;

Node *head; //헤드 포인터

void error(char *msg) {
	printf("%s", msg);
	exit(1);
}

void init_list() {
	head = NULL;
}

int size() {
	int counter = 0;
	Node *n = NULL;
	for(n=head; n!=NULL; n=n->link) {
		counter++;
	}
	return counter;
}

Node* get_entry(int index) {
	int i;
	Node *n = head;
	for(i=0; i<index; i++, n=n->link) {
		if(n==NULL) { //끝까지 탐색했을때 (찾으려는 index가 존재하지 않을때)
			return NULL;
		}
	}
	return n;
}

void replace(int index, Element e) {
	Node *n = get_entry(index);
	if(n != NULL) {
		n->data = e;
	}
}

void clear_list() {
	while(!is_empty()) {
		delete();
	}
}

int is_empty() {
	return head==NULL;
}

void insert_next(Node *before, Node *node) {
	if(node != NULL) {
		node->link = before->link;
		before->link = node;
	}
}

void insert( int pos, Element e ) {
	Node *new_node, *prev;
	new_node = (Node*)malloc(sizeof(Node));
	new_node->data = e;
	new_node->link = NULL;

	if( pos==0 ) { //가장 앞에 노드를 추가할 때

		new_node->link = head;
		head = new_node;

	} else { // 중간에 노드를 추가할 때

		prev = get_entry(pos-1); //추가하려는 인덱스의 앞 노드
		if( prev!=NULL ) {
			insert_next(prev, new_node);
		} else { // 존재하지 않는 인덱스에 추가하려고 할 때
			free(new_node);
		}

	}
}

Node* remove_next(Node *before) {
	Node *removed = before -> link;
	if( removed != NULL ) {
		before->link = removed->link;
	}
	return removed;
}

void delete( int pos ) {
	Node *prev, *removed;

	if( pos==0 && is_empty()==0 ) { //가장 앞 노드이고, 공백 리스트가 아닐때
		removed = head;
		head = head->link;
		free(removed);
	} else { //중간 노드일 때
		prev = get_entry(pos-1); //삭제할 노드의 앞 노드
		if( prev!=NULL ) {
			removed = remove_next(prev);
			free(removed);
		}
	}
}

Node* find( Element e ) {
	Node *n;
	for(n=head; n!=NULL; n=n->link) {
		if(n->data == e) {
			return n;
		}
	}
	return NULL; //탐색 실패시
}

int main() {
	int i;
	init_list();
	
	
	for(i=0; i<10; i++) {
		insert(i, i*10);
	}
	
	delete(0);
	delete(0);
	delete(0);
	delete(0);
}

성결대학교 컴퓨터 공학과 박미옥 교수님 (2021)
최영규, 『두근두근 자료구조』

본 게시글은 위 강의 및 교재를 기반으로 정리한 글입니다.

리스트

개요

리스트란?

리스트의 특징

리스트 ADT

데이터

연산

리스트 구현 개요

구현 방법의 종류

구현 (by. 배열)

특징

공백상태

포화상태

삽입 연산

삭제 연산

초기변수설정

error(char *msg)

init_list()

size()

get_entry(int index)

replace(int index, Element e)

clear_list()

is_empty()

is_full()

insert( int pos, Element e )

delete(int pos)

find( Element e )

전체 구현

구현 (by. 연결리스트)

특징

공백상태

포화상태

항목 참조(get_entry) 연산

삽입 연산

삭제 연산

초기변수 및 구조체

error(char *msg)

init_list()

size()

get_entry(int index)

replace(int index, Element e)

clear_list()

is_empty()

is_full()

insert_next( Node *before, Node *node ) & insert( int pos, Element e )

remove_next(Node *before) & delete(int pos)

find( Element e )

전체 구현

insert_next( Node before, Node node ) & insert( int pos, Element e )