스택 응용

괄호 검사

목적

• 같은 유형의 괄호가 쌍을 이루어야 한다.

• 소괄호, 중괄호, 대괄호 모두 포함

조건

1. ‘왼쪽 괄호의 개수’와 ‘오른쪽 괄호의 개수’가 같아야 한다.
2. 왼쪽 괄호는 오른쪽 괄호보다 먼저 나와야 한다.
3. 괄호 사이에는 포함 관계만 존재한다.

알고리즘

• 기본 원리
  • 왼쪽 괄호 입력 : push
  • 오른쪽 괄호 입력 : pop
• 개요
  • 문자를 저장하는 스택 준비. (공백상태)
  • 문자열에 있는 괄호를 차례대로 조사, 왼쪽 괄호 발견시 push.
  • 오른쪽 괄호 발견시 pop.
• 위배 조건
  • pop : 스택이 비어있다면 조건2 위배
  • pop : 꺼낸 괄호가 오른쪽 괄호와 짝이 맞지 않다면 조건3 위배
  • 마무리 : 마지막까지 스택이 비어있지 않다면 조건1 위배

  조건 모두 만족 ⇒ 성공 (true)

  조건 위배 ⇒ 실패 (false)

• 의사코드

  

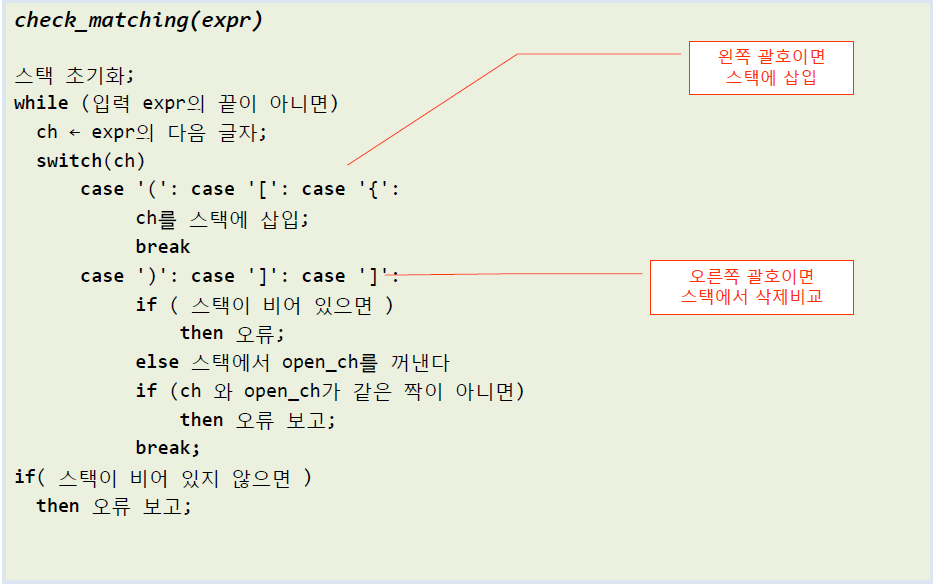
예시 : 성공

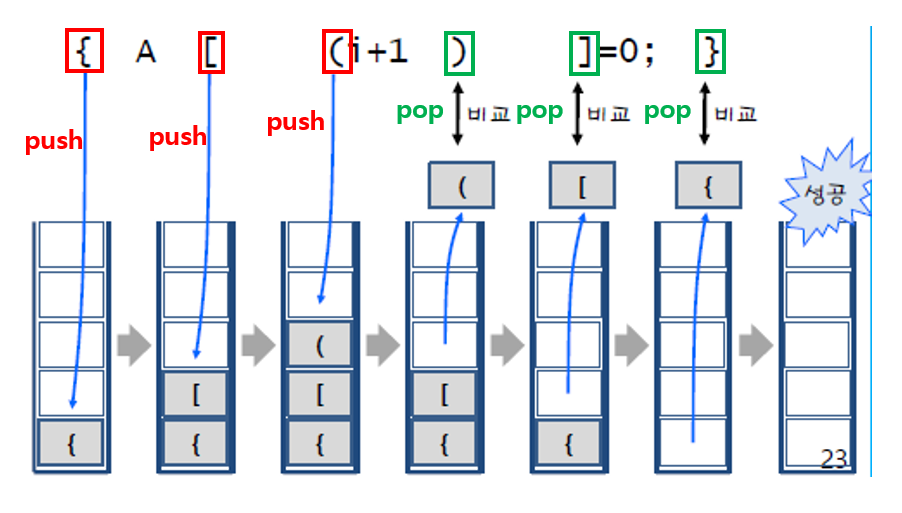
예시 : 조건 위배

코드화

#include <stdio.h>
#define MAX_SIZE 100

typedef char Element;

Element stack[MAX_SIZE];
int top;

void error(char *msg) {
	printf("%s", msg);
	exit(1);
}

void init() {
	top = -1;
}

int is_empty() {
	return top==-1;
}

int is_full() {
	return top==MAX_SIZE-1;
}

void push(Element e) {
	if(is_full())
		error("stack overflow");
	stack[++top] = e;
}

Element pop() {
	if(is_empty())
		error("왼쪽 괄호 부재"); 
	return stack[top--];
}

Element peek() {
	if(is_empty())
		error("stack underflow");
	return stack[top];
}

int size() {
	return top+1;
}

int is_right_pair(Element e) {
	if(e==')' && peek()=='(') {
		return 1;
	} else if(e=='}' && peek()=='{') {
		return 1;
	} else if(e==']' && peek()=='[') {
		return 1;
	}
	return 0;
}

int main() {
	char s[] = "[21()]";
	init();
	
	int i;
	for(i=0; s[i]!='\0'; i++) {
		char c = s[i];
		switch(c) {
			case '(' :
				push(c);
				break; 
			case '{' :
				push(c);
				break; 
			case '[' :
				push(c);
				break;
			case ')' :
				if(is_right_pair(c)) {
					pop();	
				} else {
					error("짝이 맞지 않음");
				}
				break;
			case '}' :
				if(is_right_pair(c)) {
					pop();	
				} else {
					error("짝이 맞지 않음");
				}
				break;
			case ']' :
				if(is_right_pair(c)) {
					pop();	
				} else {
					error("짝이 맞지 않음");
				}
				break;
		}
	}
	
	if(size() == 0) {
		printf("성공!");
	}else {
		printf("오른쪽 짝이 없음"); 
	}
}

수식 계산

수식의 표기방법

• 전위 (prefix)
• 중위 (infix)
• 후위 (postfix)

중위 표기법	전위 표기법	후위 표기법
2+3*4	+2*34	234*+
a*b+5	+5*ab	ab*5+
(1+2)+7	+7+12	12+7+

컴퓨터에서의 수식 계산순서

• 중위 → 후위 → 계산

후위 표기 장점

• 괄호를 사용하지 않고도 계산 가능
• 연산자의 우선순위 고려 X
• 수식을 읽으며 바로 계산 가능

후위 표기의 계산 원리

1. 전체 수식을 왼쪽에서 오른쪽으로 스캔
2. 스캔 과정에서 피연산자 검출 ⇒ 스택에 push
3. 연산자 검출 ⇒ pop 2번 (피연산자 2개 꺼냄)
4. 계산 결과 ⇒ push
5. 반복

<예시>  
### 알고리즘  <숫자 검출=""> 0 : 48 9 : 57 <문자끼리 산술연산=""> '6'-'0' ⇒ int형 6

### 구현 ```c #include #include #define MAX_SIZE 100 typedef double Element; Element stack[MAX_SIZE]; int top; void error(char *msg) { printf("%s", msg); exit(1); } void init() { top = -1; } int is_empty() { return top==-1; } int is_full() { return top==MAX_SIZE-1; } void push(Element e) { if(is_full()) error("stack overflow"); stack[++top] = e; } Element pop() { if(is_empty()) error("stack underflow"); return stack[top--]; } Element peek() { if(is_empty()) error("stack underflow"); return stack[top]; } int size() { return top+1; } int main() { char post[] = "23+4*5"; int i; for(i=0; post[i]!='\0'; i++) { char c = post[i]; double second; double first; switch(c) { case '+' : second = pop(); first = pop(); push(first+second); break; case '-' : second = pop(); first = pop(); push(first-second); break; case '*' : second = pop(); first = pop(); push(first*second); break; case '/' : second = pop(); first = pop(); push(first/second); break; default : push(c-'0'); } } printf("result: %.2f", pop()); } ```

## 중위표기 ⇒ 후위표기 변환 ### 중위 & 후위 공통점 피연산자의 순서 동일 ### 중위 & 후위 차이점 연산자의 순서만 다르다 >따라서, 연산자만 스택에 저장했다가 출력 >2+3*4 ⇒ 234\*+
### 알고리즘 1. 피연산자 검출 ⇒ 그대로 출력 2. 'top요소'보다 '우선 순위가 높은 연산자' 검출 ⇒ push 3. 'top요소'보다 '우선 순위가 낮거나 같은 연산자' 검출 ⇒ pop > 왼쪽 괄호 : 가장 낮은 우선순위의 연산자 취급 > 오른쪽 괄호 : 스택's 왼쪽 괄호 위에 쌓여있는 모든 연산자 pop 
### A*B+C 변환 예시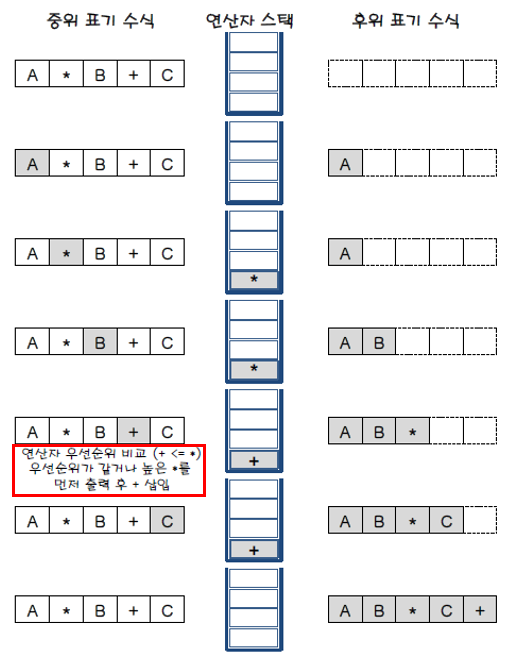 
### (A+B)*C 변환 예시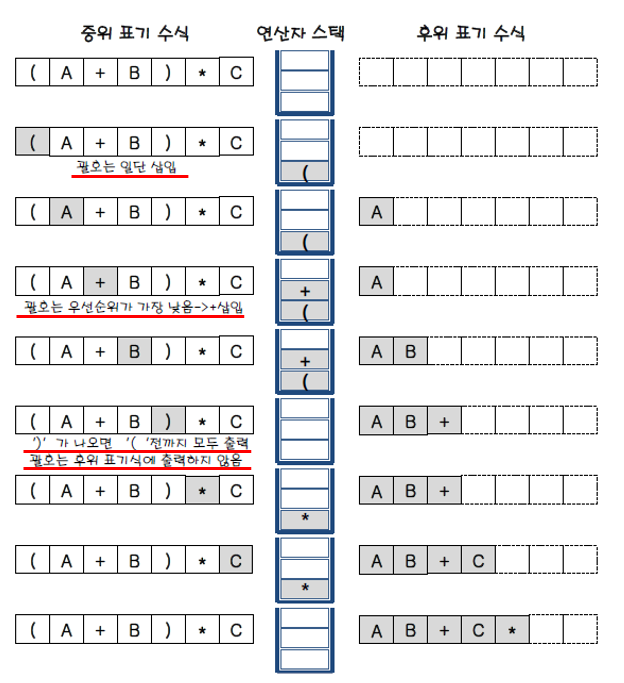 

### 구현 ```c #include #define MAX_SIZE 100 typedef char Element; Element stack[MAX_SIZE]; int top; void error(char *msg) { printf("%s", msg); exit(1); } void init() { top = -1; } int is_empty() { return top==-1; } int is_full() { return top==MAX_SIZE-1; } void push(Element e) { if(is_full()) error("stack overflow"); stack[++top] = e; } Element pop() { if(is_empty()) error("stack underflow"); return stack[top--]; } Element peek() { if(is_empty()) error("stack underflow"); return stack[top]; } int size() { return top+1; } int prior(char op) {//우선순위 반환 switch(op) { case '(': case ')' : return 0; case '+': case '-' : return 1; case '*': case '/' : return 2; } } int main() { char s[] = "(4+3+3)*5+(4/2)"; int i; for(i=0; s[i]!='\0'; i++) { char c = s[i]; char pushed_op; if(c>='0' && c<='9') { // 숫자라면 즉시 출력 printf("%c", c); } else if(c=='(') { push(c); } else if(c==')') { while(!is_empty()) { //스택이 빌때까지 pushed_op = pop(); if(pushed_op == '(') break; //(가 발견될때 까지 printf("%c", pushed_op); } } else if(c=='+' || c=='-' || c=='*' || c=='/') { //일반 연산자일때 while(!is_empty()) { pushed_op = peek(); if(prior(c) < prior(pushed_op)) { printf("%c", pop()); } else { push(c); break; } } } } while(!is_empty()) { //마지막으로 스택에 남아있는 연산자 출력 printf("%c", pop()); } } ```

---

• 성결대학교 컴퓨터 공학과 박미옥 교수님 (2021)
• 최영규, 『두근두근 자료구조』

본 게시글은 위 강의 및 교재를 기반으로 정리한 글입니다.