캐시 메모리

캐시 메모리란?

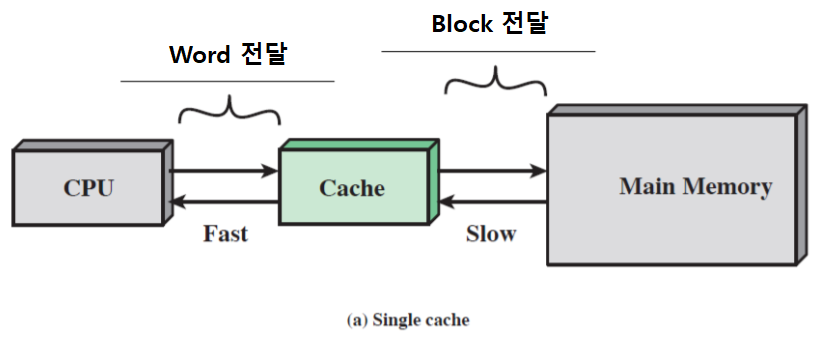
• 캐시 메모리란, 속도가 빠른 장치와 느린 장치에서 속도 차이에 따른 병목 현상을 줄이기 위한 메모리이다.

캐시 메모리를 사용하는 이유

• RAM은 꽤 빠른 메모리 장치이지만, CPU에 비하면 그 속도가 너무 느리다.
• 따라서 RAM보다 속도가 빠른 캐시 메모리를 사용한다.

CPU ↔ RAM 간의 캐시 메모리와 같이, RAM ↔ HDD 간의 캐시 메모리도 존재한다.
이것을 ‘디스크 캐시’라고 한다.

기본 작동 원리

1. CPU가 주기억장치에서 저장된 데이터를 읽어올 때, 자주 사용하는 데이터를 캐시 메모리에 저장한다.
2. CPU가 동일한 데이터를 주기억장치가 아닌 캐시 메모리에서 먼저 가져온다.

캐시 메모리가 주기억장치보다 빠르기 때문에, 더 빠르게 데이터에 접근할 수 있다.

하지만 캐시 메모리는 용량이 훨씬 적고, 비용도 비싸다.

캐시 vs 주기억장치

주기억장치의 데이터 저장방식

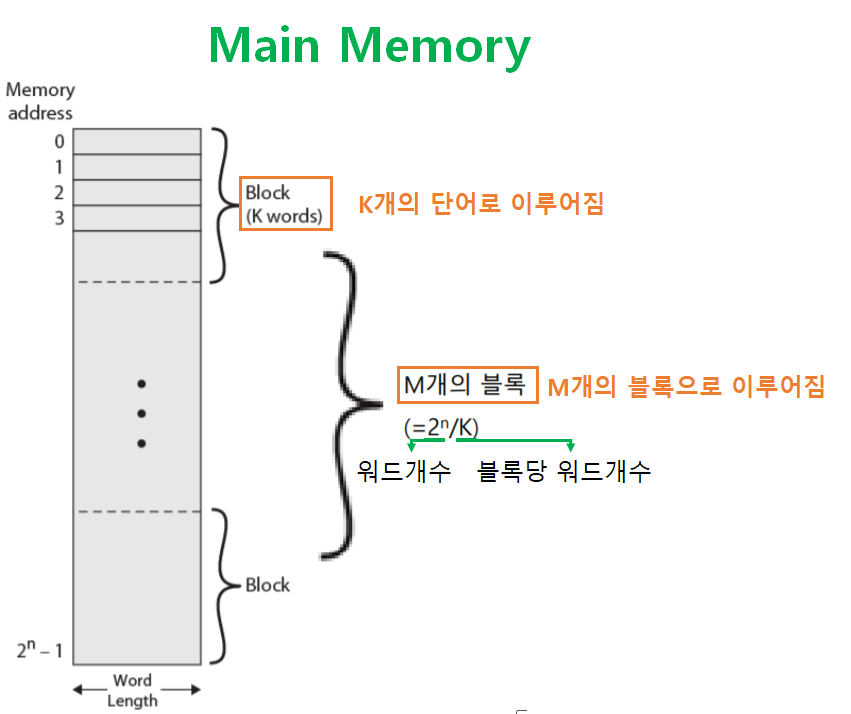
• 주기억장치에는 총 2^n 개의 단어(Word) 가 저장되어 있다.
• 그리고 K 개의 단어를 묶어, 하나의 블록(Block) 을 구성한다.
• 따라서 전체 블록의 개수는 (2^n) / K 와 같다.

캐시 메모리의 데이터 저장방식

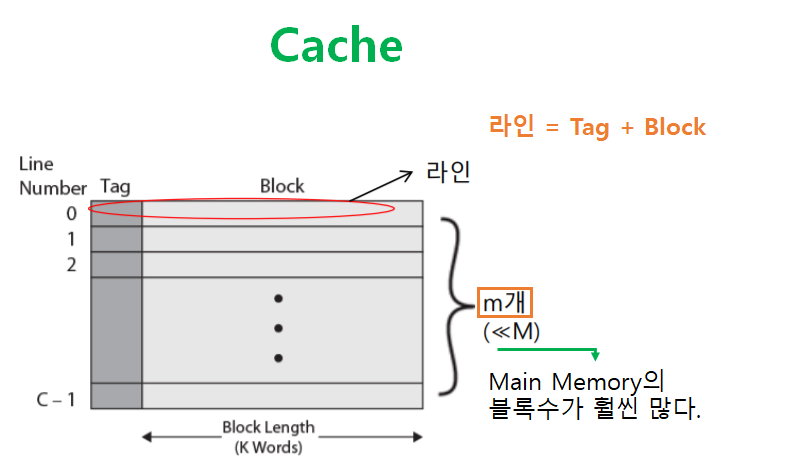
• 캐시 메모리는 C - 1 개의 라인(Line) 이 저장되어 있다.
• 하나의 라인은 Tag 와 블록 으로 구성된다.
  • Tag : 주기억장치에서의 Block 위치 정보
  • 블록 : 주기억장치에서 k 개의 단어로 구성된 블록

즉 정리하자면 아래 그림과 같다.

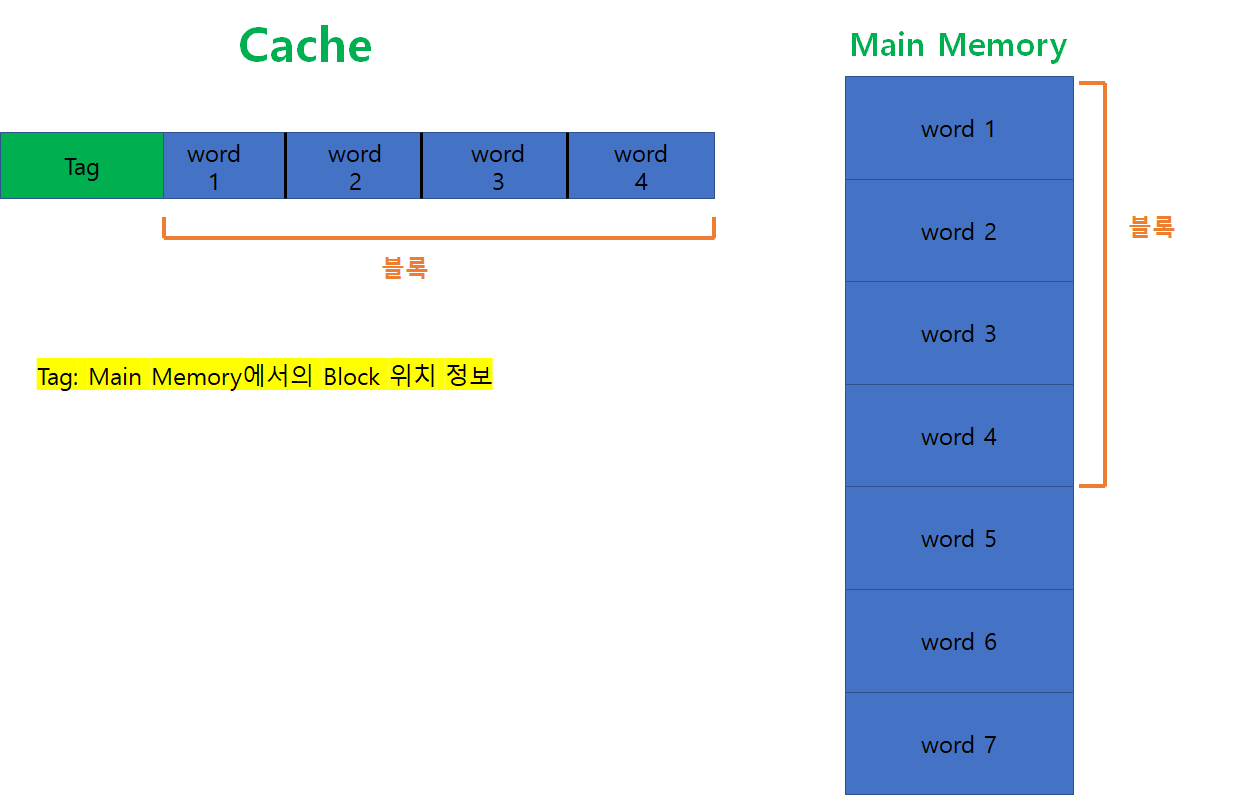
캐시 메모리의 종류

CPU에는 캐시 메모리가 2~3개 정도 사용된다.

• L1 캐시 메모리
• L2 캐시 메모리
• L3 캐시 메모리

L1 → L2 → L3 순으로 속도가 느려지고, 용량은 증가한다.

또한 L1 → L2 → L3 순으로 CPU가 접근한다.

만약 L1에서 원하는 데이터를 찾지 못한 경우, L2에 접근하는 방식

캐시 메모리 작동 원리

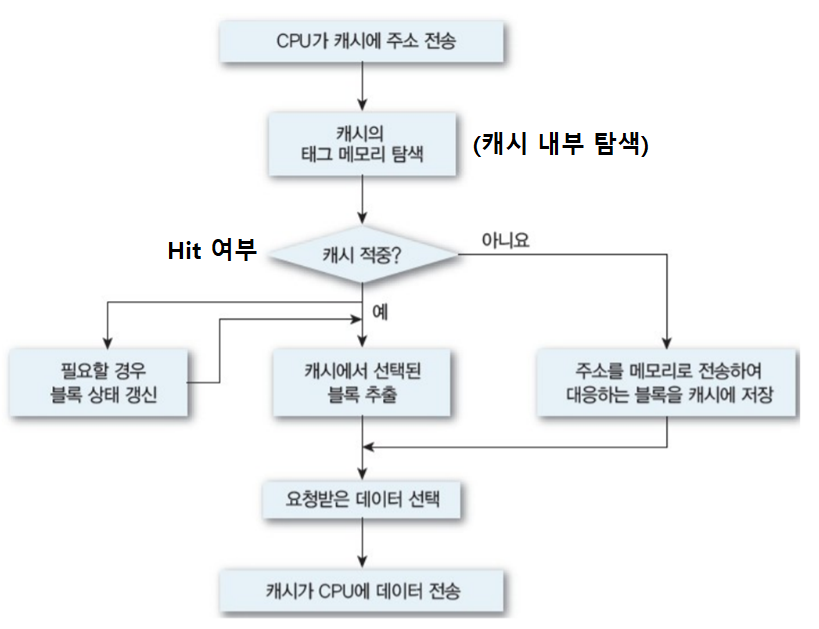
참조 지역성 원리

• 참조 지역성 원리란?
  • 대부분의 경우, 순차적으로 프로그램이 진행된다.

    프로그램이 실행되는 동안 순차적이지 않은 분기/호출 명령은 작은 부분을 차지한다.

  • 또한 한정된 수의 함수(프로시저)를 계속 호출하는 경향이 있다.
  • 그리고 서로 인접한 데이터에 대해 처리하는 로직이 많이 존재한다.
  • 이러한 특징을 “참조 지역성 원리” 라고 하며, 이것을 최대한 활용해서 ‘캐시 Hit 확률’ 을 높일 수 있다.

• 캐시 메모리는 참조 지역성 원리에 의해 설계되었다.

  

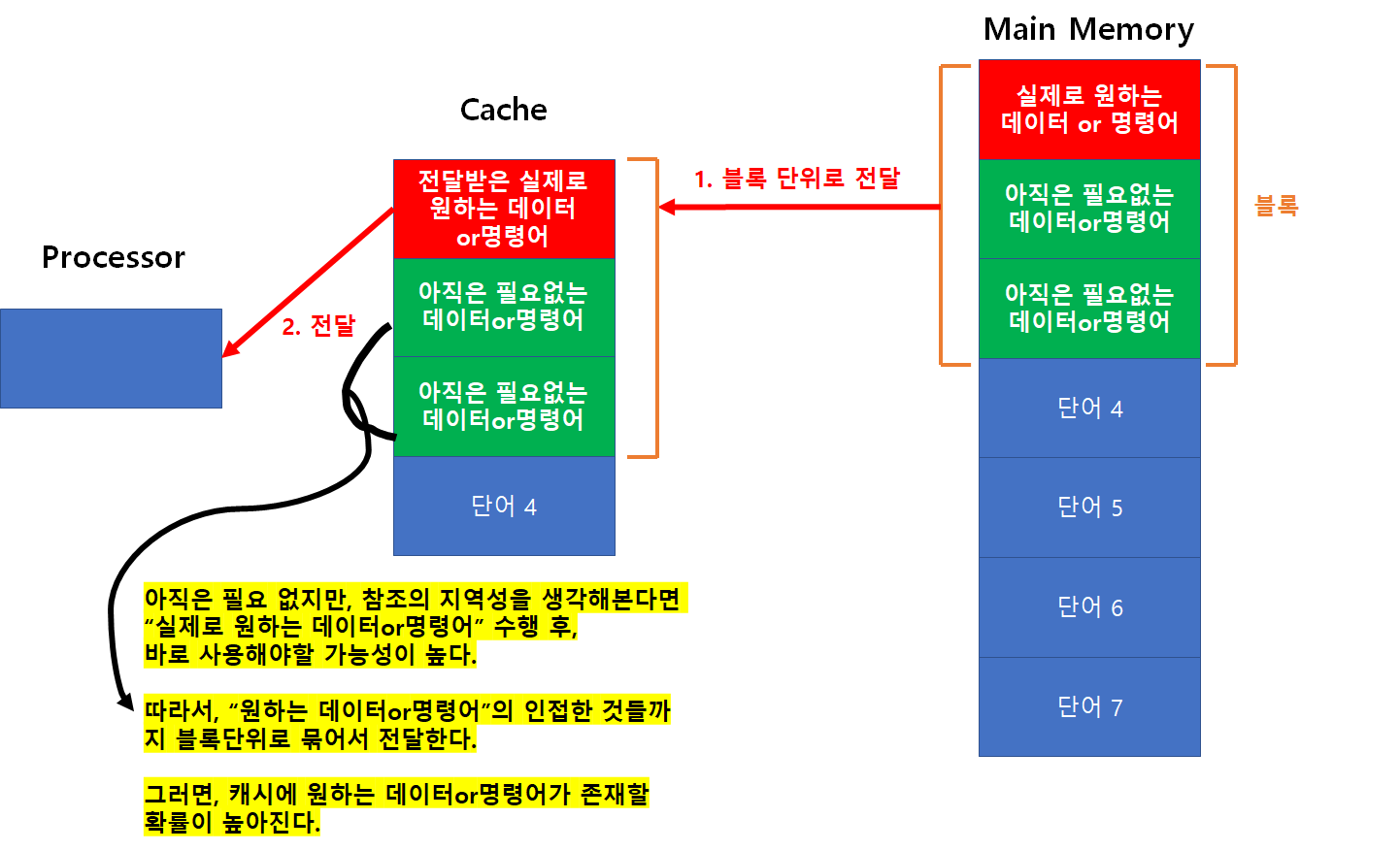
참조 지역성 원리 - 공간적 지역성

• 프로세스가 명령어나 데이터들을 순차적으로 액세스하는 경향을 말한다.
• 즉, 명령어 A를 실행하면 물리적으로 인근에 저장된 명령어를 다음에 실행할 가능성이 높다는 특징이다.

참조 지역성 원리 - 시간적 지역성

• 프로세서가 최근에 사용됐던 기억 장소들을 액세스하는 경향을 말한다.
• 즉, for나 while 같은 반복문에 사용하는 조건 변수 처럼 한번 참조된 데이터는 다시 참조될 가능성이 높다는 특징이다.

캐시 미스의 종류

Cold Miss

• 해당 메모리 주소를 처음 불러서 발생하는 미스이다.

Conflict Miss

• 캐시 메모리에 A와 B 데이터를 저장해야 하는데, A와 B가 같은 캐시 메모리 주소에 할당되어 있어서 발생하는 미스이다.
• 주로 직접 사상(매핑) 방식에서 자주 발생한다.

  직접 사상에 대해선 후반부에 다룬다.

Capacity Miss

• 캐시 메모리의 공간이 부족해서 발생하는 미스이다.

Conflict Miss 는 캐시 공간이 충분하지만 데이터를 적재하는 방식 때문에 발생한다.
Capacity Miss 는 캐시 공간 자체가 부족해서 발생한다.

캐시 크기를 키우면 Hit 확률이 높아지지 않을까?

캐시 크기를 키워서 Miss 문제를 해결하면, 아래와 같은 문제가 발생한다.

• 캐시 크기가 커질수록 캐시 접근속도가 저하된다.
• 캐시 크기가 커질수록 전력소모가 커진다.

캐시 매핑 방식 - 직접 사상 (Direct Mapped Cache)

직접 사상 (Direct Mapped Cache) 이란?

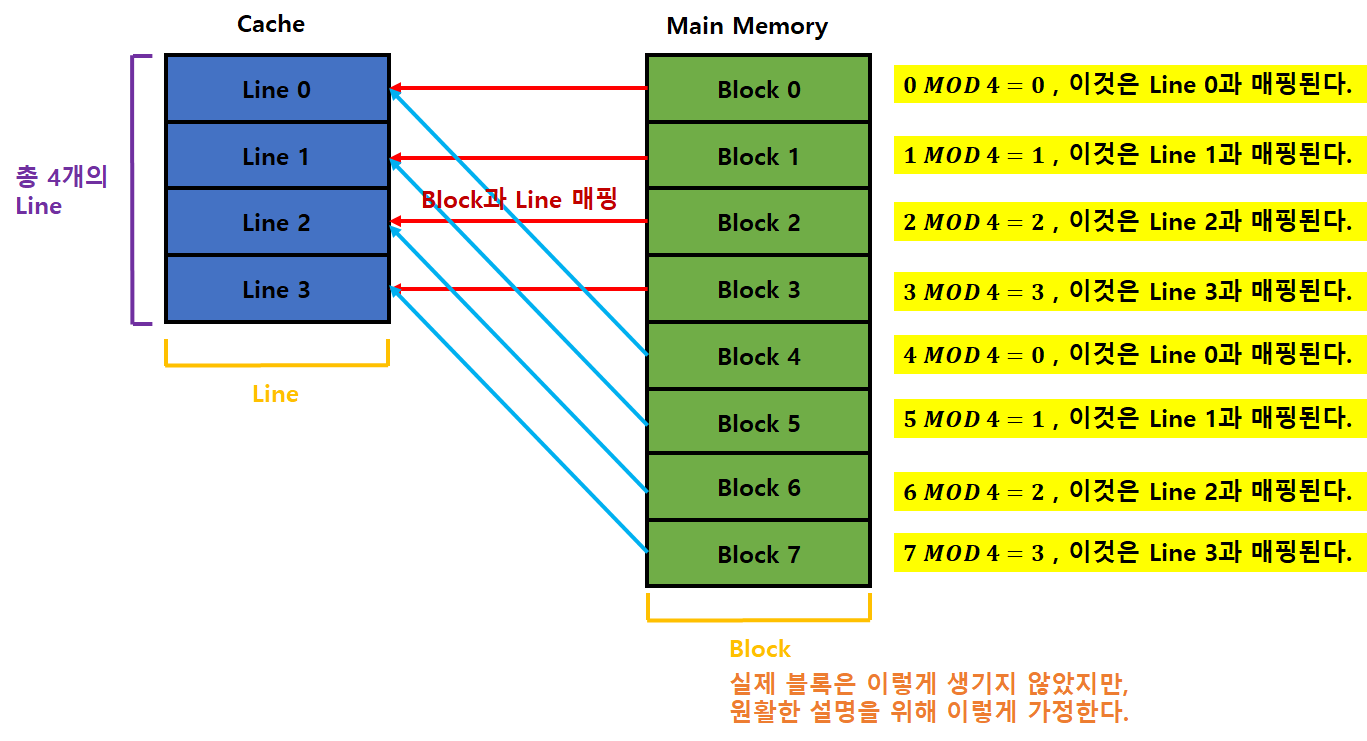
• 가장 기본적인 구조로, DRAM(주기억장치)의 여러 주소가 캐시 메모리의 한 주소에 대응되는 “다대일 방식” 이다.
• 즉 주기억장치의 각 블록들은 각자 지정된 라인으로 매핑된다.
• 매핑시 사용되는 함수는 아래와 같다.
  • i = j MOD m
  • i : 매핑할 캐시 라인 번호
  • j : 매핑될 주기억장치 블록 번호
  • m : 캐시의 총 라인 개수

캐시와 주기억장치 간의 관계

조금 더 자세히 설명하자면 아래와 같다.

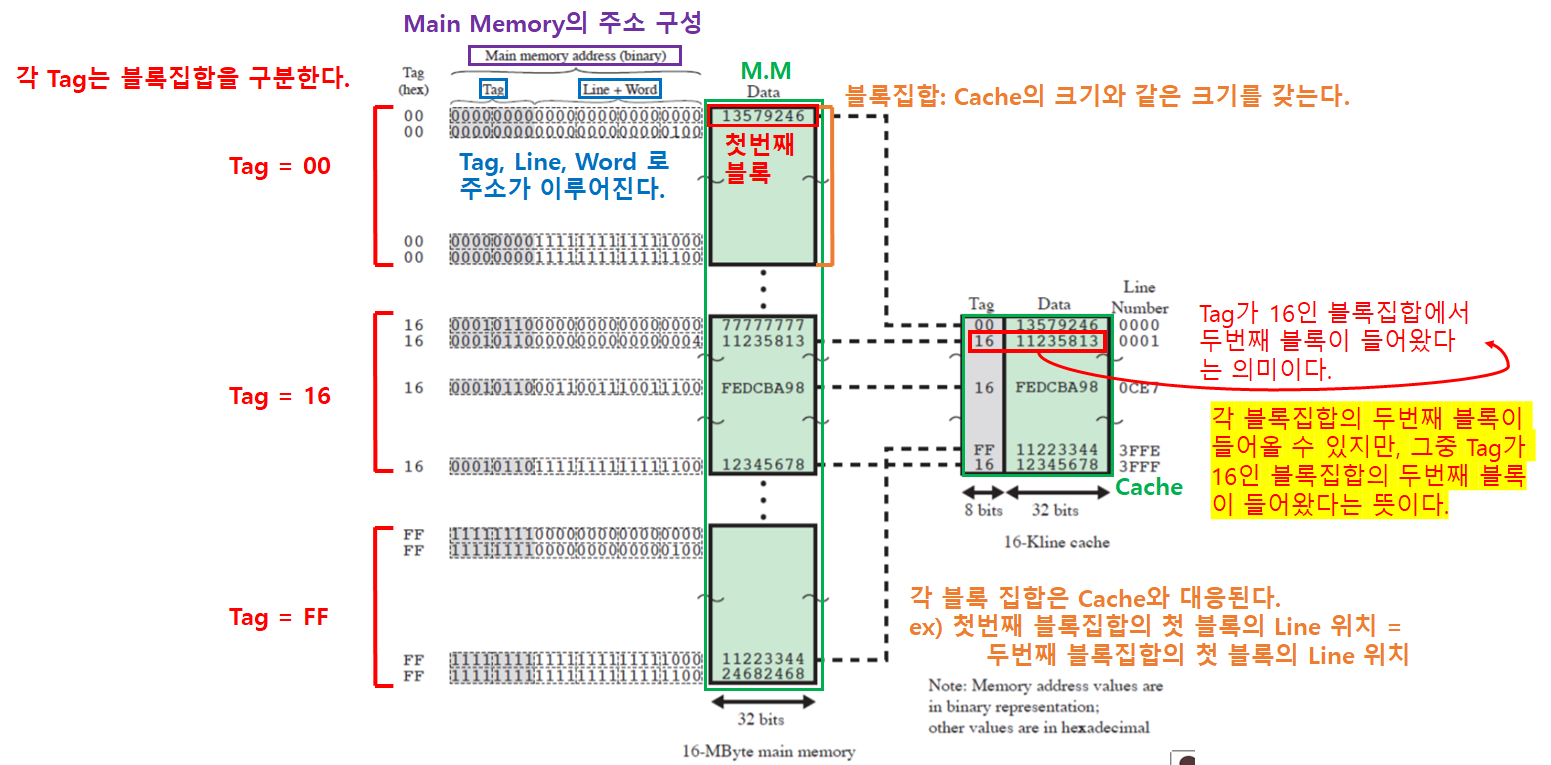
• 블록집합 = 주기억장치의 블록들을 캐시 크기에 맞춰 묶은 것
• 주기억장치의 주소는 Tag , Line주소 , Word주소 로 이뤄진다.
  • Tag : 각 블록집합을 구분
  • Line주소 : 한 블록 집합 내에서 블록을 구분
  • Word주소 : 한 블록 내에서 단어(Word)를 구분
• 각 블록집합의 같은 순서의 블록끼리 캐시 라인을 경합한다.
  • 1번 라인에 들어갈 수 있는 블록은 각 블록집합의 첫번째 블록 이다.
  • 따라서 블록집합 A의 첫번째 블록 과 블록집합 B의 첫번째 블록 은 함께 캐시에 저장될 수 없다.

장단점

• 장점
  • 간단하고 구현 비용이 적게 든다.
• 단점
  • 블록집합의 블록마다 들어갈 수 있는 캐시 위치가 고정되어 있다.
    → 따라서 캐시 적중률이 낮다.
  • 캐시에 빈 공간이 있어도 지정된 위치가 있기 때문에 miss가 발생할 가능성이 높다.

캐시 매핑 방식 - 완전 연관 사상 (**Fully Associative Cache**)

완전 연관 사상 (**Fully Associative Cache**) 이란?

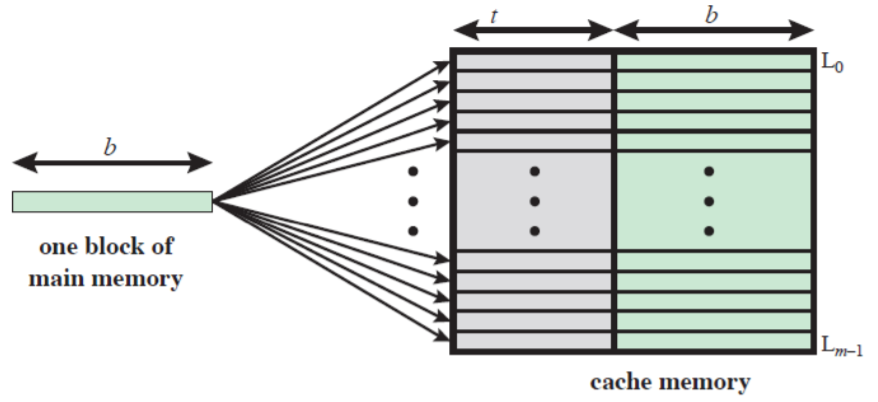
• 빈 캐시 메모리가 있으면, 마음대로 주소를 저장하는 방식이다.
• 즉 주기억장치의 블록을 아무 캐시 라인에 저장할 수 있다.
• 주기억장치의 모든 블록을 Tag 만으로 구분한다.

캐시와 주기억장치 간의 관계

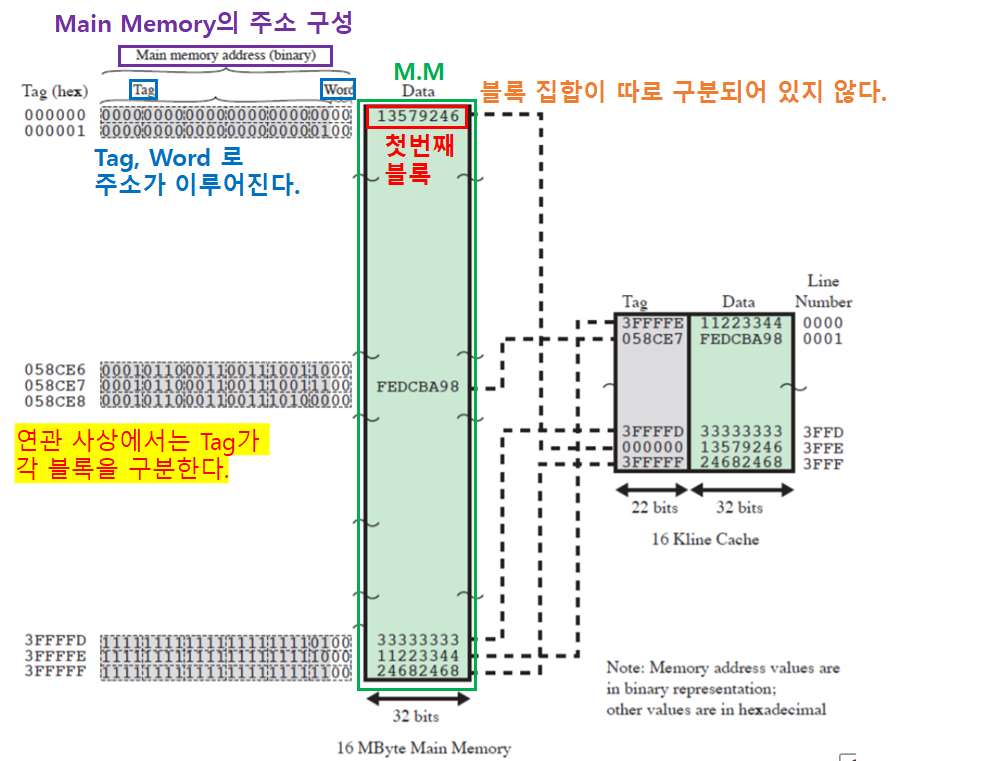
• 블록 집합이 오직 1개이다.

장단점

• 장점
  • 캐시에 저장하는 조건이나 규칙이 없어, 저장하기에 매우 간단하다.
• 단점
  • 캐시 저장에 필요한 조건이나 규칙이 없기 때문에, 데이터를 찾을 때 캐시의 모든 라인을 살펴봐야 한다.
  • 태그들을 병렬로 검사하기 위한 회로가 추가적으로 필요해, 특수 메모리 구조를 사용해야 하고 가격이 매우 비싸다.

캐시 매핑 방식 - 세트 연관 사상 (**Set Associative Cache**)

세트 연관 사상 (**Set Associative Cache**) 이란?

• 직접 사상과 완전 연관 사상을 합친 방식이다.
• 캐시가 여러 개의 세트 들로 나눠지고, 각 세트 들은 여러 라인들로 구성된다.

세트 연관 사상 방식의 종류

세트 연관 사상 방식의 종류는 총 2개가 있다.

• v 연관 사상 캐시

  

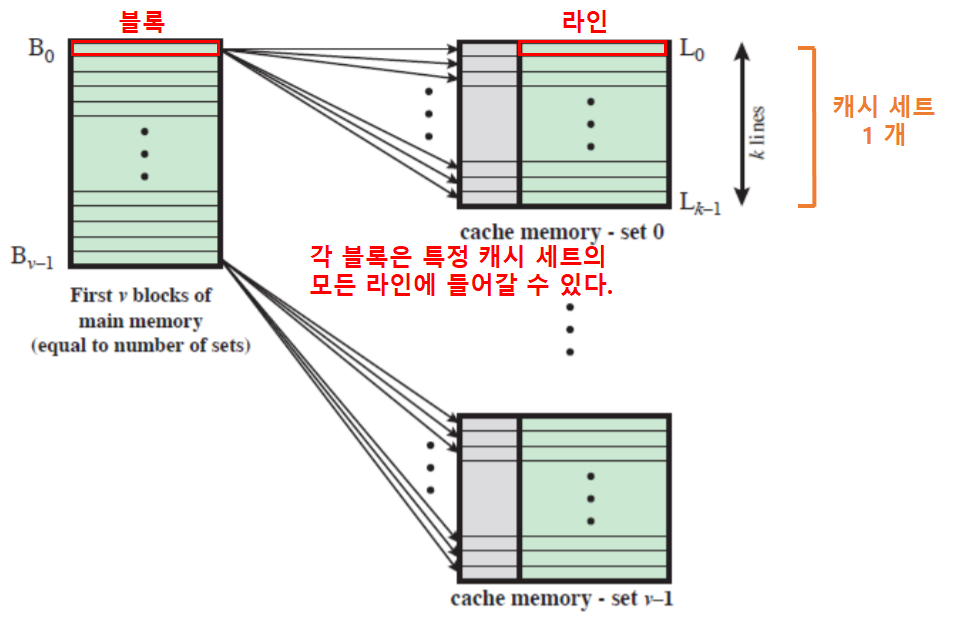
  • v개의 연관 캐시 들로 구현할 수 있다.
  • 하나의 블록이 한 세트의 모든 라인에 들어갈 수 있는 방식

• k 직접 사상 캐시

  

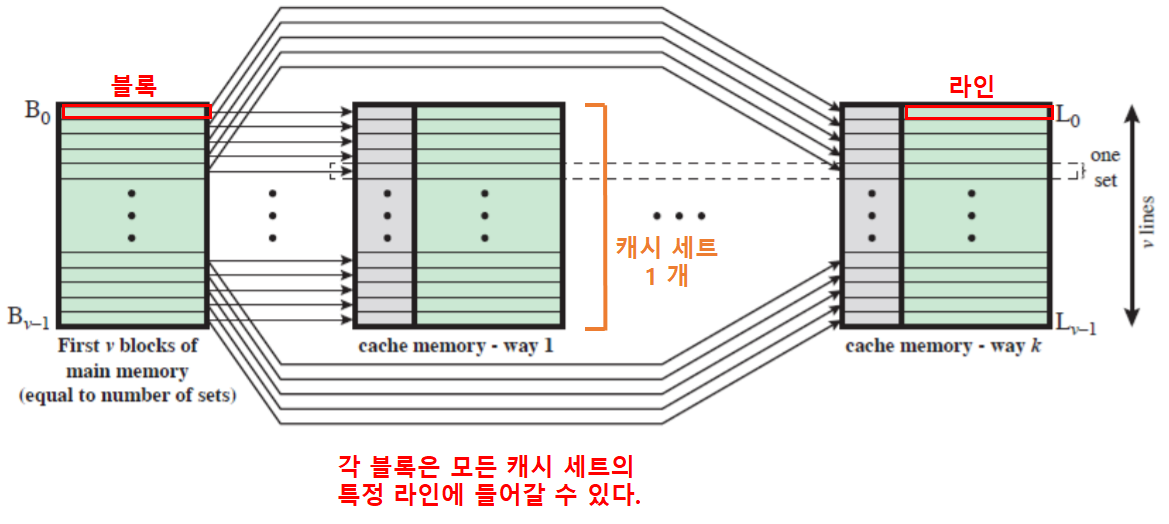
  • k개의 직접 캐시 들로 구현할 수 있다.
  • 하나의 블록이 모든 세트의 한 라인에 들어갈 수 있는 방식

캐시와 주기억장치 간의 관계

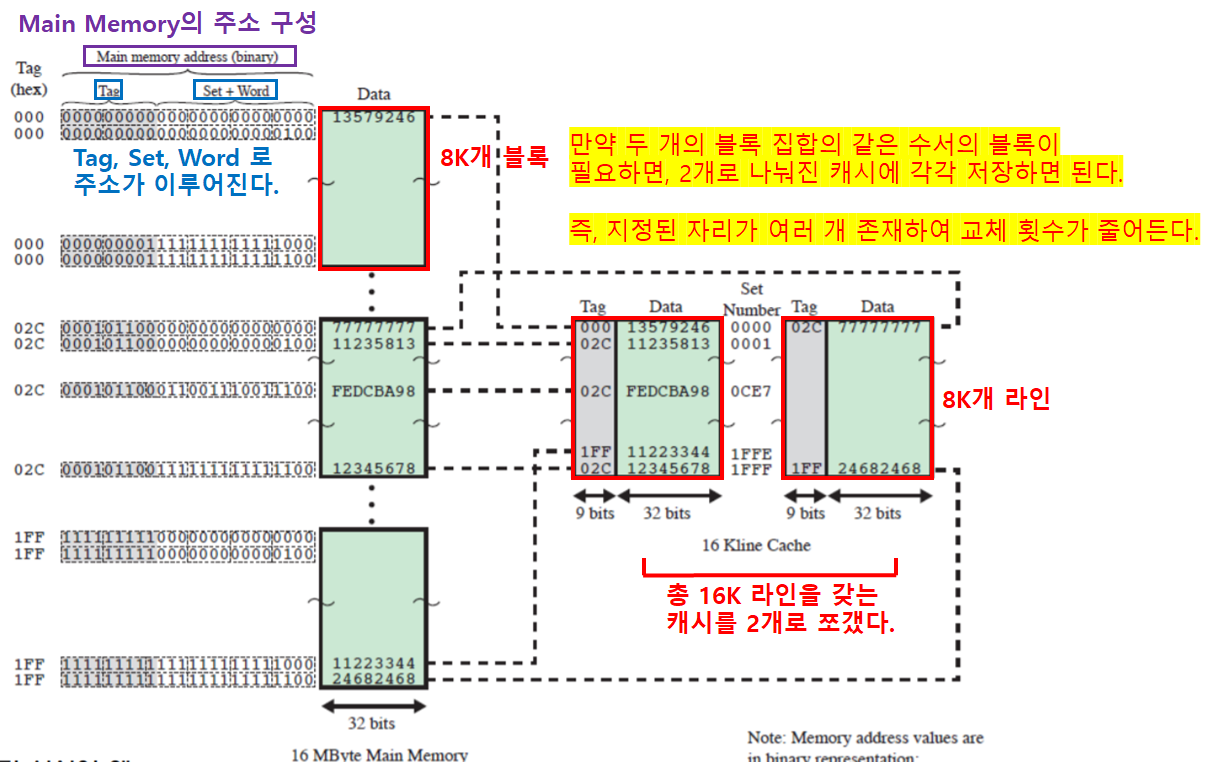
• 캐시가 쪼개져, 여러 세트로 구성된다.
• 주기억장치의 각 블록 세트의 크기와 각 세트의 크기가 동일하다.

장단점

• 완전 연관 사상에 비해, 저장속도는 느리지만 비용이 저렴하고 조회 속도도 빠르다.
• 직접 연관 사상에 비해, 복잡하지만 적중률이 높다.

다른 사상들과의 관계 : v 연관 사상 캐시

• 만약 하나의 세트의 크기가 전체 캐시만큼 크다면? → 완전 연관 사상과 동일해진다.
  • v 연관 사상 방식은 특정 세트의 모든 라인에 블록이 매핑된다.
    하지만 세트가 하나밖에 없다면, 각 블록이 캐시의 모든 라인에 매핑될 수 있다.
  • 결국 모든 블록은 모든 라인에 들어갈 수 있어진다.
• 만약 하나의 세트 크기가 1개의 라인만큼 작다면? → 직접 사상과 동일해진다.
  • 결국 각 블록이 들어갈 라인이 정해지게 된다.

다른 사상들과의 관계 : k 직접 사상 캐시

• 만약 하나의 세트의 크기가 전체 캐시만큼 크다면? → 직접 사상과 동일해진다.
  • k 직접 사상 방식은 각 세트의 특정 라인에 블록이 매핑된다.
    하지만 세트가 하나밖에 없다면, 각 블록이 매핑될 라인이 정확하게 정해지게 된다.
  • 결국 각 블록이 들어갈 라인이 정해지게 된다.
• 만약 하나의 세트 크기가 1개의 라인만큼 작다면? → 완전 연관 사상과 동일해진다.
  • 결국 모든 블록은 모든 라인에 들어갈 수 있어진다.