고정 소수점 & 부동 소수점

컴퓨터에서 실수를 표현하는 방법들

컴퓨터에서 실수를 표현하는 방법에는 아래 두가지 방식이 존재한다.

• 고정 소수점
• 부동 소수점

고정 소수점 (Fixed Point)

고정 소수점이란?

소수점이 찍힐 위치를 미리 정해놓고, 소수를 표현하는 방식이다.

부호와 정수 부분과 소수 부분으로 구성된다.

표현 예시

-3.625 을 고정 소수점으로 표현하면 아래와 같다.

• 부호 부분
  • - → 1 (2진수)
• 정수 부분
  • 3 → 2^1 + 2^0 → 000 0000 0000 0011 (2진수 - 15비트)
• 소수 부분
  • 625 → (2^-1) + (2^-3) → 1010 0000 0000 0000 (2진수 - 16비트)

따라서 이를 합쳐서 표현하면 아래와 같다.

1 000 0000 0000 0011 . 1010 0000 0000 0000

장단점

• 장점
  • 연산을 처리할 때, 정수 연산과 똑같이 처리할 수 있다. 따라서 부동 소수점 방식보다 연산이 빠르다.
  • 실수를 정수부와 소수부로 표현하기 때문에 단순하다.
• 단점

  • 정수부와 소수부를 표현하기 위한 비트가 정해져있다. 따라서 담을 수 있는 수의 범위가 작다.

    소수부에서 오직 3개의 비트만 사용하고, 나머지 비트를 모두 정수 비트로 사용하는 식으로 공간을 활용할 수 없다.

부동 소수점 (Floating Point)

부동 소수점이란?

실수를 가수부 와 지수부 로 표현하는 방식이다.

• 가수부 : 실수의 실제값을 표현하는 부분
• 지수부 : 크기를 표현하는 부분으로, 소수점의 위치를 나타낸다.

지수의 값에 따라 소수점이 움직이는 방식 이다.

즉 소수점의 위치가 고정되어 있지 않다.

정규화된 표현

지수의 값에 따라, 동일한 수를 여러가지 방식으로 표현할 수 있다.

예를 들면 아래와 같다.

• 0.1001 * 2^5
• 0.01001 * 2^6
• 10.01 * 2^3

위 3가지 표현 모두 동일한 이진수이다.

따라서 부동소수점의 수를 통일되게 표현할 수 있는 방법이 필요하다!

이것이 바로 정규화된 표현 이다.

정규화된 표현으로 만들기 위한 규칙은 아래와 같다.

• 무조건 정수부분은 1(이진수) 하나만 와야한다.
• +- 1.xxx...x * 2^E 와 같은 형태를 갖춰야 한다.

정규화된 표현으로 이진수를 표현하면 아래와 같다.

• 정규화가 된 경우 → 1.001 * 2^4
• 정규화가 되지 않은 경우 → 100.1 * 2^2

가수부

정규화된 표현으로 인해, 무조건 가장 왼쪽에 있는 비트는 1(이진수) 이 된다.

따라서 가장 왼쪽에 있는 비트는 생략할 수 있다.

지수부 (바이어스된 표현)

지수는 부호를 가지므로, 이에 대한 표현이 필요하다.

예를 들어, (2^-3) 에서 - 를 표현할 수 있어야 한다.

그리고 그 방법이 바로 바이어스된 표현 이다.

지수부 필드에 저장할 때, 바이어스화 시켜서 저장하게 된다.

• 지수부 필드에 값을 저장할 때 → (본래 지수값) + 127
• 지수부 필드에서 값을 추출할 때 → (바이어스된 지수값) - 127

보통 바이어스화할 때, 127를 더한다.

예를 들어보면 아래와 같다.

• 지수값

  

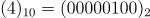
• 바이어스된 지수 표현

  

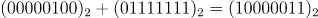
따라서 최종적으로 지수부 필드에 저장되는 값은 10000011 이다.

예제) 10진수를 부동소수점으로 표현하기

십진수 -13.625 를 부동소수점 형식으로 표현해보자.

1. 13.625 를 정규화된 이진수로 치환한다.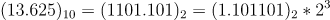

   

   참고로 소수점 이하를 이진수로 치환할 때는, 2를 곱하면서 나온 1의 자리수를 취하면 된다.

   • 0.625 * 2 = 1.25 → 1 을 추출하고, 소수점의 첫번째 자리에 배치
   • 0.25 * 2 = 0.5 → 0 을 추출하고, 소수점 두번째 자리에 배치
   • 0.5 * 2 = 1.0 → 1 을 추출하고, 소수점 세번째 자리에 배치
2. 십진수 -13.625 가 음수이므로, 부호비트는 1로 설정한다.
3. 정규화된 이진수 1.101101 에서 가장 좌측의 1 은 생략한 나머지 101101 을 가수부 필드에 저장한다.
4. 지수부 필드에는 2^3 의 지수인 3 을 저장해야 한다. 3 을 이진수로 표현하면 011 이다. 또한 바이어스 시켜야하므로 127 의 이진수인 01111111 를 더한다.
   그 결과는 00000011 + 01111111 = 10000010 이다.

5. 따라서 결과는 아래와 같다.

   

예제) 32비트 부동소수점 값을 십진수로 변환하기

32비트 부동소수점 0 10000011 101 0000 0000 0000 0000 0000 를 10진수로 변환해보자.

1. 부호비트가 0 이므로, 양수이다.

2. 가수부 필드 값이 101 이므로, 1.101 로 표현할 수 있다. (생략된 1을 다시 가져옴)
   그리고 1.101 을 십진수로 변환하면 아래와 같다.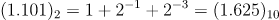

   

3. 지수부 필드 값인 10000010 에 바이어스를 복구하기 위해 01111111 을 빼고, 다시 십진수로 변환한다.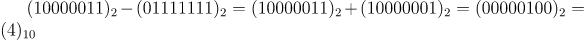

   

   • 즉 지수부의 값은 4 이다.

4. 따라서 결과는 아래와 같다.

   

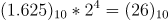
장단점

• 장점
  • 표현할 수 있는 수의 범위가 넓어진다. (현재 대부분 시스템에서 활용 중)
• 단점
  • 오차가 발생할 수 있다.