패리티 비트 & 해밍 코드
패리티 비트
패리티 비트란?
- 정보 전달 과정에서 오류가 생겼는지 검사하기 위해 추가하는 비트이다.
- 전송하고자 하는 데이터에 1비트를 더해서 전송한다.
패리티 비트의 종류
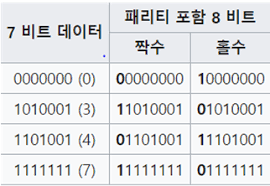
- 짝수 패리티
- 데이터의 모든
1의 개수를 짝수로 맞춰야 한다. - 예시
- 보내려는 데이터 :
1011101(총 5개의1) - 보내려는 데이터의
1의 개수가 총 5개로 홀수이다. - 따라서 가장 왼쪽에
1의 값을 갖는 비트를 추가 해서 짝수로 맞춰야 한다. - 짝수 패리티 적용 시 :
11011101(총 6개의1)
- 보내려는 데이터 :
만약 보내려는 데이터의
1의 개수가 이미 짝수라면,0을 가장 왼쪽에 추가한다. - 데이터의 모든
- 홀수 패리티
- 데이터의 모든
1의 개수를 홀수로 맞춰야 한다. - 예시
- 보내려는 데이터 :
1010011(총 4개의1) - 보내려는 데이터의
1의 개수가 총 4개로 짝수이다. - 따라서 가장 왼쪽에
1의 값을 갖는 비트를 추가 해서 홀수로 맞춰야 한다. - 홀수 패리티 적용 시 :
11010011(총 5개의1)
- 보내려는 데이터 :
만약 보내려는 데이터의
1의 개수가 이미 짝수라면,0을 가장 왼쪽에 추가한다. - 데이터의 모든
오류 검출 원리
짝수 패리티일 때, 데이터가 중간에 손실되었다고 가정해보자.
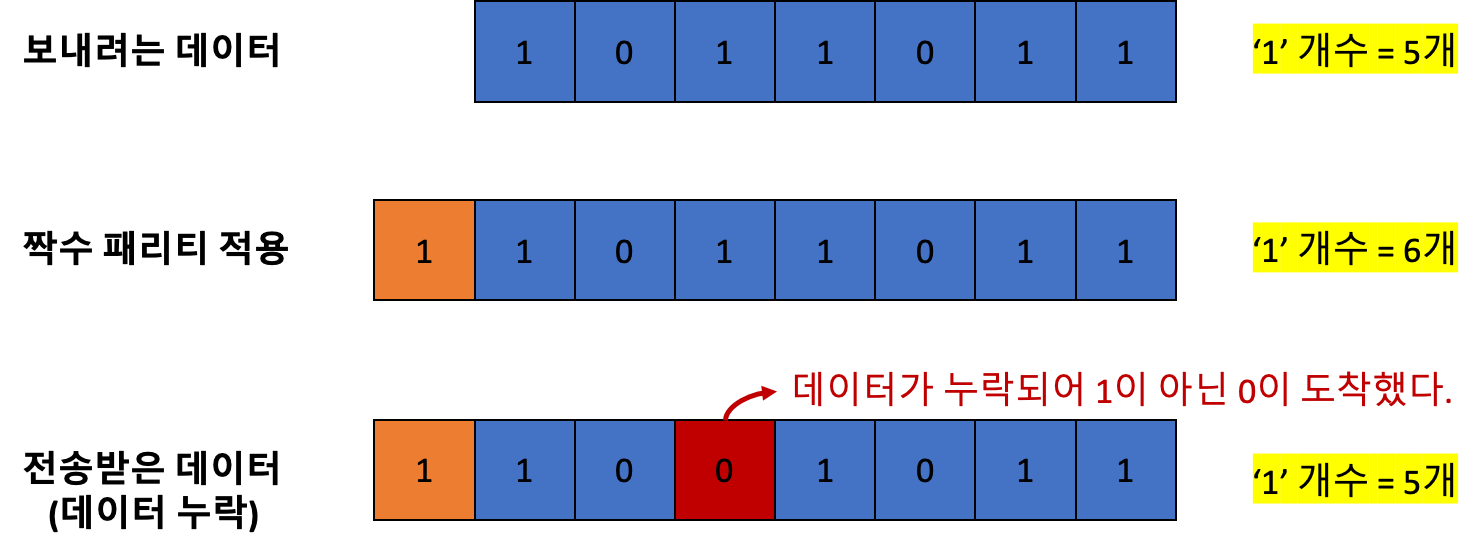
짝수 패리티를 적용했으므로, 전송받은 데이터의 1 개수가 짝수 이어야 한다.
하지만 데이터가 일부 누락되어 최종적으로 전송받은 데이터의 1 개수가 홀수 이다.
따라서 오류가 발생했음을 알아낼 수 있다.
패리티 비트의 한계점
- 만약 2비트의 데이터가 손실되면 알아차릴 수 없다.
- 오류를 검출할 수 있기만 할 뿐, 수정할수는 없다.
해밍 코드
해밍 코드란?
- 데이터를 전송할 때, 1비트의 에러를 정정할 수 있는 자기 오류정정 코드를 말한다.
- 1개 이상의
패리티 비트를 사용한다. - 먼저 패리티비트를 보고, 1비드에 대한 오류를 정정할 곳을 찾아내고 수정할 수 있다.
전송할 데이터 비트사이에패리티 비트를 끼워넣어 해밍코드를 만들 수 있다.
해밍 코드 생성 과정
각 과정은 아래에서 자세히 설명한다.
- 필요한
패리티 비트의 개수를 계산한다.- 규칙에 따라,
패리티 비트를 위치시킨다.- 나머지 공간에
데이터 비트를 위치시킨다.
1. 필요한 패리티 비트 개수 계산

패리티 비트의 개수를 계산하는 공식은 위와 같다. 위 공식을 만족하는 p 를 찾아내면 된다.-
만약
d (데이터 비트 개수)가 8이라고 한다면 아래와 같이 계산할 수 있다.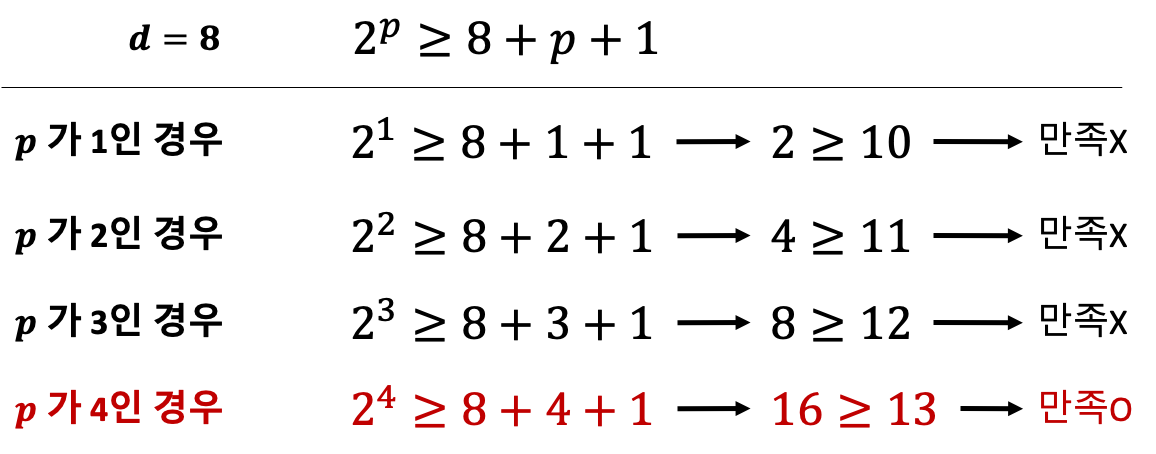
- 따라서 필요한 최소
패리티 비트개수는 4개다.
- 따라서 필요한 최소
2. 패리티 비트 위치
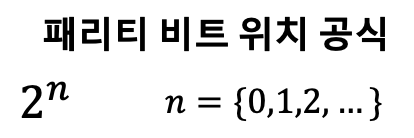
- 위 공식에 따라,
패리티 비트를 삽입하면 된다. -
만약
데이터 비트개수가 8개고패리티 비트개수가 4개라면, 아래와 같이 삽입할 수 있다.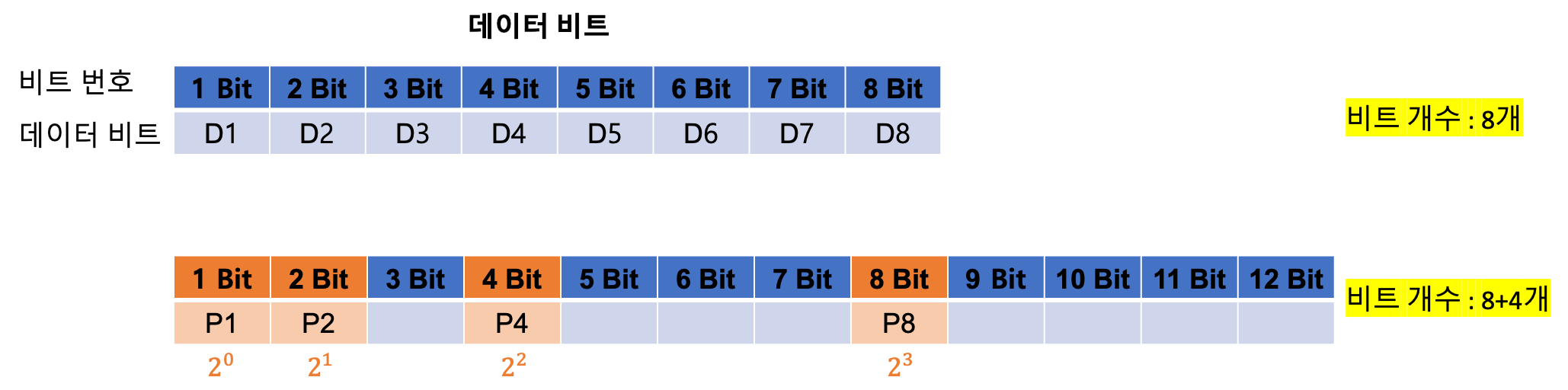
3. 데이터 비트 삽입
-
이제
데이터 비트를 순서대로 위치시키면 된다.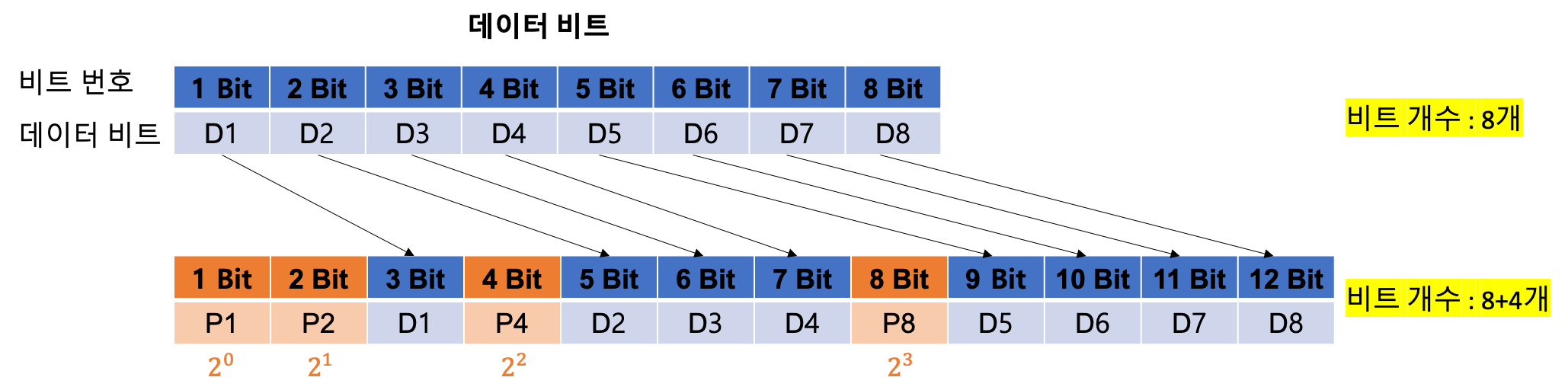
최종적으로 완성된 데이터
패리티 비트 의 값 설정
각 패리티 비트 들의 값은 ‘십진수의 Bit 위치 번호’를 이진수로 변환하고, 관련된 위치들의 비트를 확인해서 ‘홀수 패리티’나 ‘짝수 패리티’를 만족 시키면 된다.
한 단계씩 자세히 알아보자.
-
먼저 아래 그림처럼 각 비트 순서를 2진수로 바꾼다.
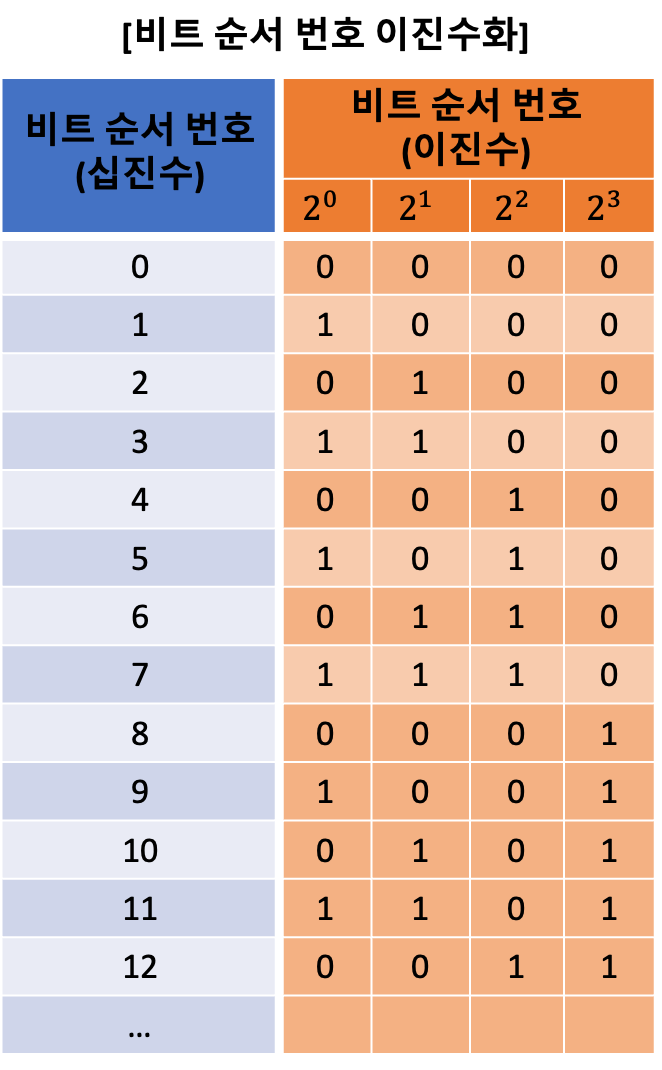
- 값을 구할 패리티 비트의 순서 번호에 따라, 확인할 비트들을 선택하면 된다.
- 예를 들어, 총 12비트 길이에서 “
2^0위치의 패리티 비트의 값”을 계산할 때 필요한 “비트들의 위치”를 구하는 방법은 아래와 같다.
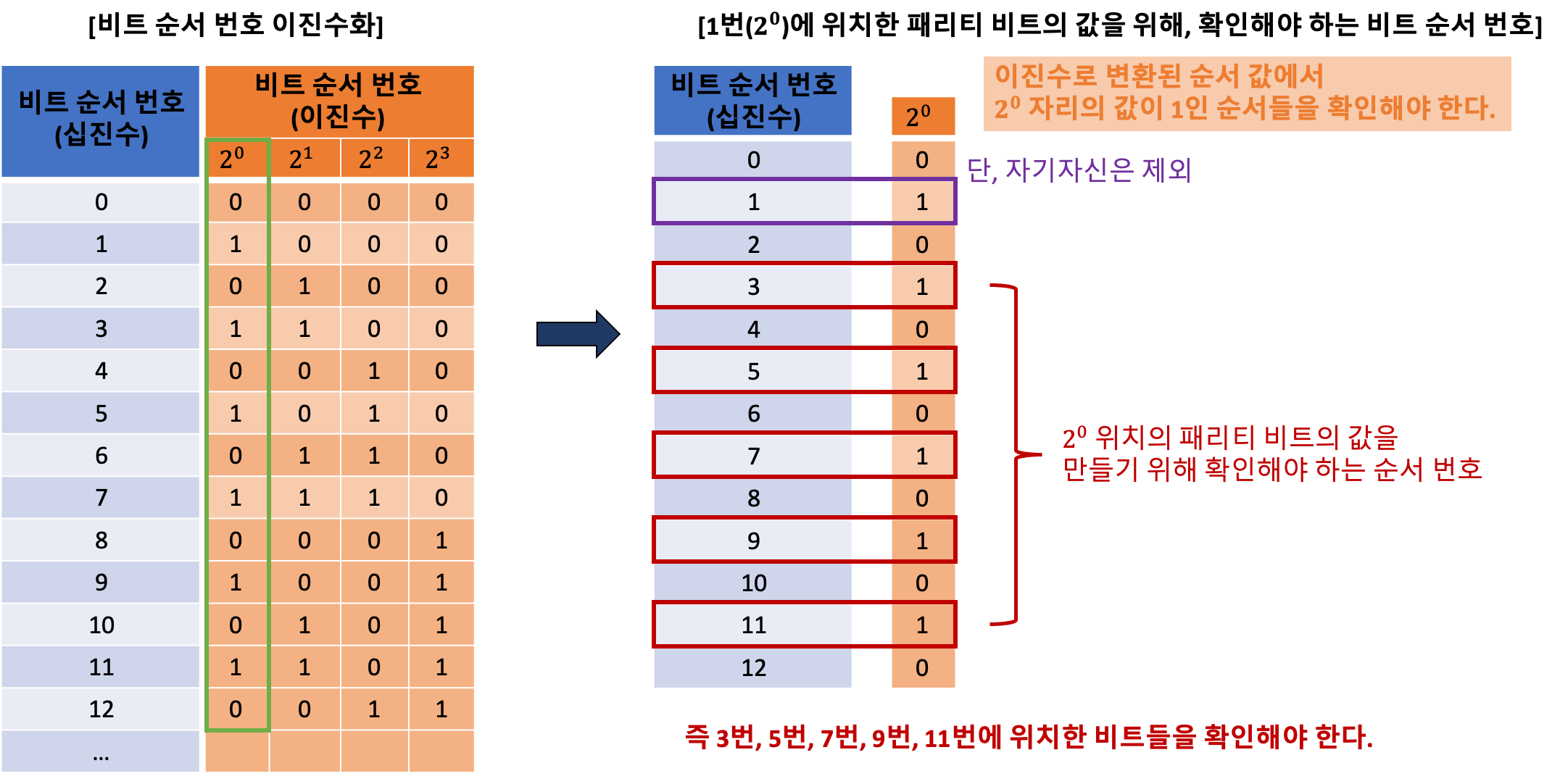
- 예를 들어, 총 12비트 길이에서 “
-
따라서 확인해야 하는 비트들은 아래와 같다.
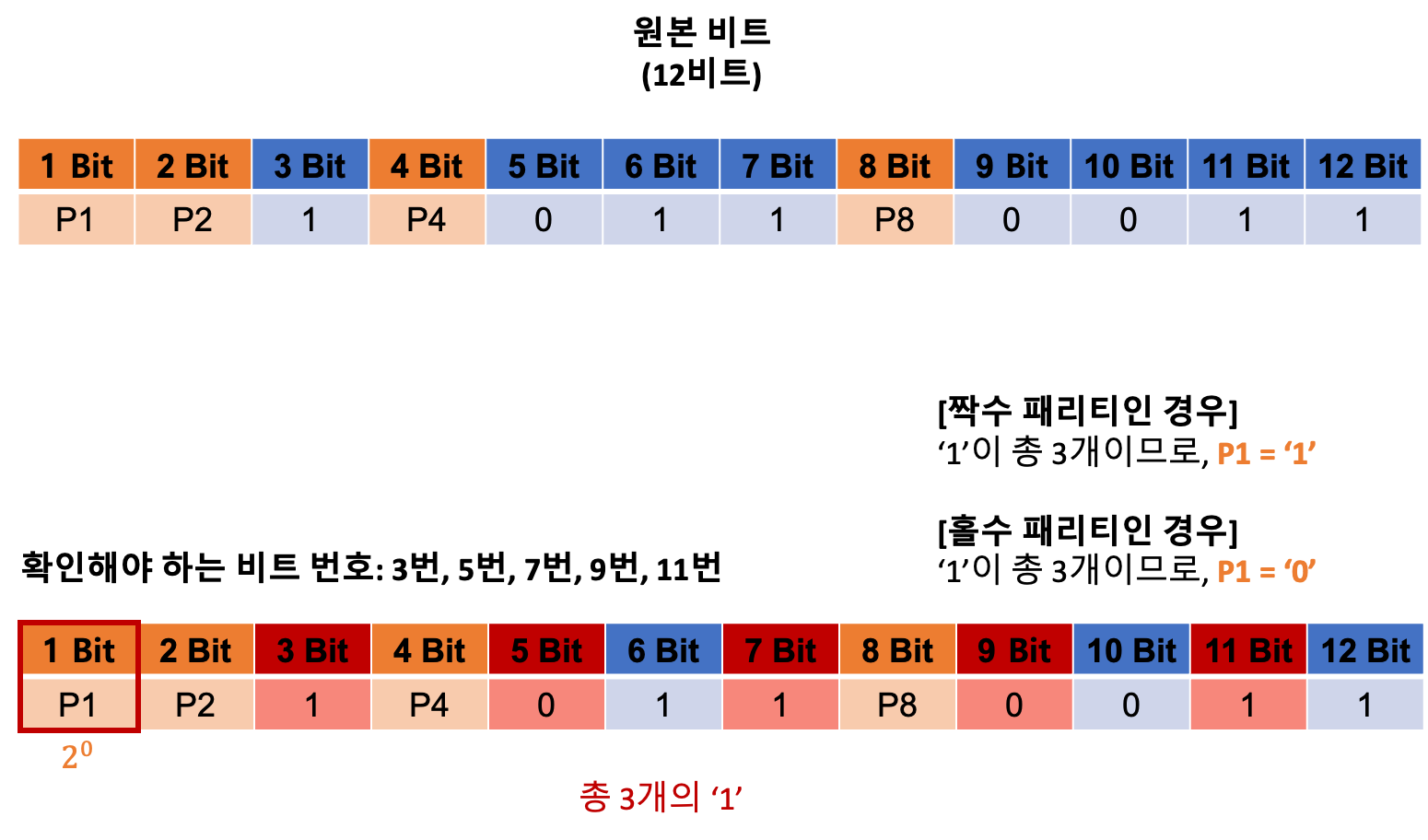
- 3번, 5번, 7번, 9번, 11번에 위치한 비트를 확인해서 ‘짝수/홀수 패리티’ 규칙을 만족시킬 수 있도록
1번째 비트에 위치한 패리티 비트의 값을 설정 하면 된다.
- 3번, 5번, 7번, 9번, 11번에 위치한 비트를 확인해서 ‘짝수/홀수 패리티’ 규칙을 만족시킬 수 있도록
- 모든 패리티 비트에 대해 이 과정을 반복하면 된다.
아래는 각 패리티 비트 들의 체킹 범위를 보기 좋게 정리한 표이다.
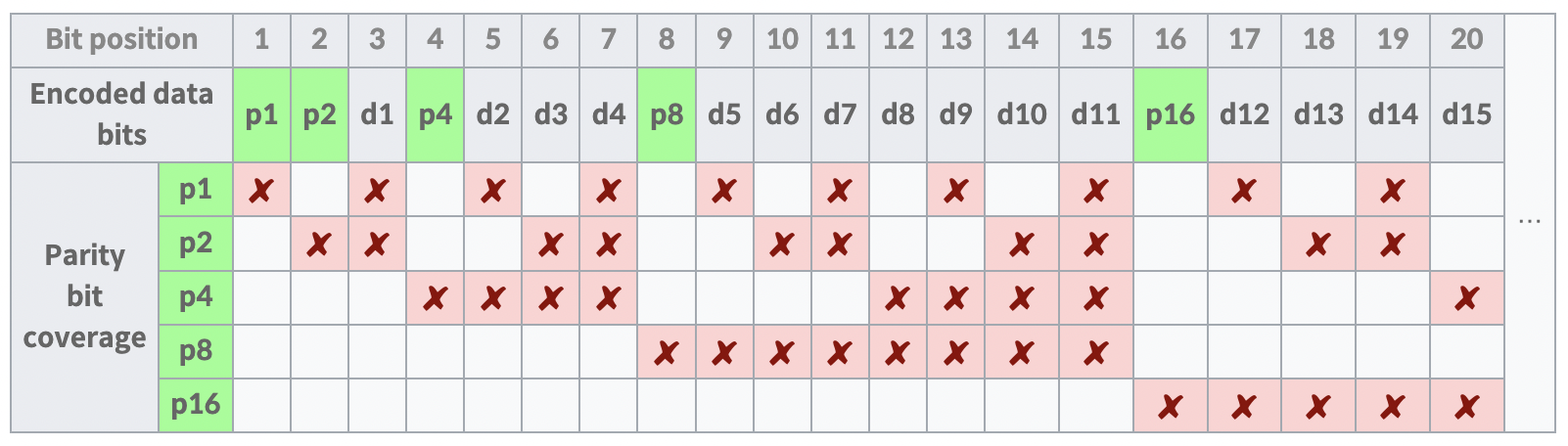
위 표에 따라서, 비트들을 선택해 ‘짝수/홀수 패리티’ 조건을 맞춰 패리티 비트 의 값을 지정하면 된다.
해밍코드의 오류 검출, 수정
이번에는 해밍코드에서 발생한 오류를 검출하고 수정해보자.
오류가 발생한 비트의 위치를 계산하는 과정은 아래와 같다.
-
각
패리티 비트가 갖는 범위 마다 ‘1’의 개수를 센다.위
패리티 비트들의 체킹 범위 도표를 참고하자. -
짝수 패리티의 경우, ‘1’의 개수가 짝수라면 결과값을
0, 홀수라면1로 설정한다.짝수 패리티의 경우, 오류가 발생했을 때 ‘1’의 개수가 홀수이다.
즉, 오류 발생 시 결과를1로 설정한다. -
홀수 패리티의 경우, ‘1’의 개수가 짝수라면 결과값을
1, 홀수라면0로 설정한다.홀수 패리티의 경우, 오류가 발생했을 때 ‘1’의 개수가 짝수이다.
즉, 오류 발생 시 결과를1로 설정한다. - 각 결과값을
패리티 비트의 위치에 따라 배치하고, 배치된 숫자(이진수)를 십진수로 변환한다. - 변환된 십진수 값이 오류가 발생한 비트의 위치가 된다.
- 따라서 해당 위치의 비트값을 NOT 연산하면 오류를 수정할 수 있다.
하나씩 자세히 알아보자.
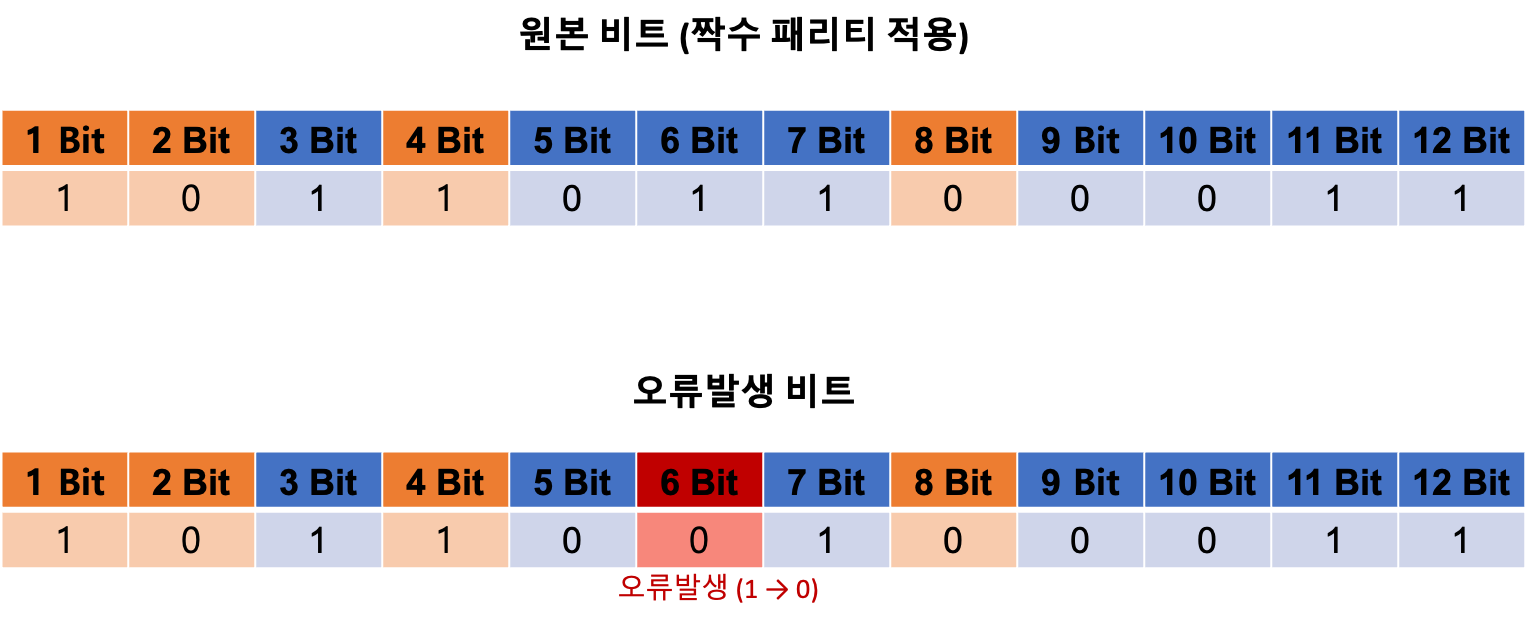
먼저 원본 비트의 오류 발생 여부를 살펴보자.

- 각 패리티 비트 (
2^0,2^1,2^2,2^3,2^4번째 비트) 마다, 관련된 비트들의 값을 취합한다. - 그리고 각각 ‘1’의 개수를 센다.
-
만약 ‘1’의 개수가 짝수라면
0, 홀수라면1를 결과값으로 갖는다. (짝수 패리티의 경우)다시 말하지만 홀수 패리티라면, 짝수일 때
1, 홀수일 때0이다. - 결과값을 십진수로 변환한다.
- 십진수가 0이므로 오류가 발생하지 않았다고 판단한다.
이번에는 오류가 발생한 경우를 살펴보자.

- 6번째 비트에
1이 아닌0이 오면서 오류가 발생했다. - 각 패리티 비트를 검사한 결과,
2^1과2^2번째 패리티 비트 범위의 ‘1’ 개수가 3개로 홀수가 나왔다. - 따라서 결과값을 각각
1로 설정했다. - 결과값을 10진수로 변환하면 6 이 된다. 따라서 오류가 발생한 위치가 6번째 비트라는 것을 알 수 있고, 이진수 값을 가지므로 NOT 연산을 통해 오류를 수정할 수 있다.
홀수 패리티가 적용된 경우, 결과값 설정을 반대로 하여 동일하게 오류를 검출할 수 있다.
홀짝 연산
홀수 패리티나 짝수 패리티를 검사하기 위해, ‘1’의 개수를 세고 홀짝 여부를 판단해야 하는 경우가 많다.
이 경우, XOR 연산을 통해 쉽게 홀짝 여부를 판단 할 수 있다.
- 각 비트의 값을 모두 XOR 연산한 결과가 0 이라면, ‘1’의 개수가 짝수라는 뜻이다.
- 각 비트의 값을 모두 XOR 연산한 결과가 1 이라면, ‘1’의 개수가 홀수라는 뜻이다.
XOR 연산을 사용해, 01100101 의 ‘1’의 개수 홀짝 여부를 판단해보자.
0 ⊕ 1 ⊕ 1 ⊕ 0 ⊕ 0 ⊕ 1 ⊕ 0 ⊕ 1 = 0 (⊕ : XOR 연산 기호)
그러므로 01100101 에서 출현한 '1'의 개수는 짝수이다.
이번에는 01100001 의 ‘1’의 개수 홀짝 여부를 판단해보자.
0 ⊕ 1 ⊕ 1 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 0 ⊕ 1 = 1 (⊕ : XOR 연산 기호)
그러므로 01100101 에서 출현한 '1'의 개수는 홀수이다.
